Giáo án Chuyên đề về chuyển động cơ học môn vật lý 9

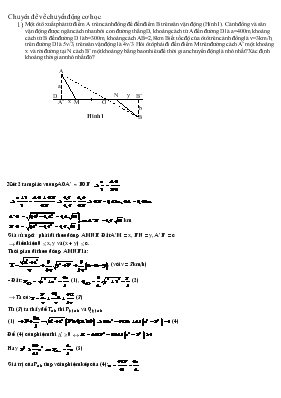
Chuyên đề về chuyển động cơ học
Một ôtô xuất phát từ điểm A trên cánh đồng để đến điểm B trên sân vận động (Hình 1). Cánh đồng và sân vận động được ngăn cách nhau bởi con đường thẳng D, khoảng cách từ A đến đường D là a=400m, khoảng cách từ B đến đường D là b=300m, khoảng cách AB=2,8km. Biết tốc độ của ôtô trên cánh đồng là v=3km/h, trên đường D là 5v/3, trên sân vận động là 4v/3. Hỏi ôtô phải đi đến điểm M trên đường cách A’ một khoảng x và rời đường tại N cách B’ một khoảng y bằng bao nhiêu để thời gian chuyển động là nhỏ nhất? Xác định khoảng thời gian nhỏ nhất đó?
a
D
A’
x
M
y
B’
N
O
b
B
A
Hình 1
XÐt 2 tam gi¸c vu«ng AOA’ ~ BOB’ 
km
Gi¶ sö ng­êi ph¶i ®i theo ®­êng AMNB. §Æt A’M = x, B’N = y, A’B’ = c 
® ®iÒu kiÖn 0 £ x, y vµ (x + y) £ c.
Thêi gian ®i theo ®­êng AMNB lµ: 
, (víi v = 3km/h)
- §Æt: (1), (2)
® Ta cã: (3)
Tõ (3) ta thÊy ®Ó Tmin th× P(x) min vµ Q(y) min
(1) (4)
§Ó (4) cã nghiÖm th× D’ ³ 0 « 
Hay (5)
Gi¸ trÞ cña Pmin øng víi nghiÖm kÐp cña (4):
T­¬ng tù ta cã: (6)
Thay (5) vµ (6) vµo (3) ta ®­îc: 
Thay sè ta cã: , ,0,6939h=41ph38s.
Một tàu điện đi qua một sân ga với vận tốc không đổi và khoảng thời gian đi qua hết sân ga (tức là khoảng thời gian tính từ khi đầu tàu điện ngang với đầu sân ga đến khi đuôi của nó ngang với đầu kia của sân ga) 18 giây. Một tàu điện khác cũng chuyển động đều qua sân ga đó nhưng theo chiều ngược lại, khoảng thời gian đi qua hết sân ga là 14 giây. Xác định khoảng thời gian hai tàu điện này đi qua nhau (tức là từ thời điểm hai đầu tàu ngang nhau tới khi hai đuôi tàu ngang nhau). Biết rằng hai tàu có chiều dài bằng nhau và đều bằng một nửa chiều dài sân ga.
- Gọi chiều dài sân ga là L, khi đó chiều dài mỗi tầu điện là L/2.
- Theo bài ra, trong thời gian t1 = 18s tầu điện thứ nhất đi được quãng đường là: 
 L + L/2 = 3L/2.
 Dó đó, vận tốc của tầu điện thứ nhất là : 
- Tương tự, vận tốc tàu thứ hai là : .
- Chọn xe thứ hai làm mốc. Khi đó vận tốc của tàu thứ nhất so với tàu thứ hai là:
- Gọi thời gian cần tìm là t. Trong thời gian đó, theo đề bài, đầu tàu thứ nhất đi được quãng đường bằng hai lần chiều dài mỗi tàu, tức là bằng L. 
 Vậy : 
3) Một cậu bé đi lên núi với vận tốc 1m/s. Khi còn cách đỉnh núi 100m, cậu bé thả một con chó và nó bắt đầu chạy đi chạy lại giữa cậu bé và đỉnh núi. Con chó chạy lên đỉnh núi với vận tốc 3m/s và chạy lại phía cậu bé với vận tốc 5m/s. Tìm quãng đường mà con chó đã chạy được từ lúc được thả đến lúc cậu bé lên tới đỉnh núi.
4) Một hành khách đi dọc theo sân ga với vận tốc không đổi v = 4km/h. Ông ta chợt thấy có hai đoàn tàu hoả đi lại gặp nhau trên hai đường song với nhau, một đoàn tàu có n1 = 9 toa còn đoàn tàu kia có n2 = 10 toa. Ông ta ngạc nhiên rằng hai toa đầu của hai đoàn ngang hàng với nhau đúng lúc đối diện với ông. Ông ta còn ngạc nhiên hơn nữa khi thấy rằng hai toa cuối cùng cũng ngang hàng với nhau đúng lúc đối diện với ông. Coi vận tốc hai đoàn tàu là như nhau, các toa tàu dài bằng nhau. Tìm vận tốc của tàu hoả
5) Một người đứng cách con đường một khoảng 50m, ở trên đường có một ô tô đang tiến lại với vận tốc 10m/s. Khi người ấy thấy ô tô còn cách mình 130m thì bắt đầu ra đường để đón đón ô tô theo hướng vuông góc với mặt đường. Hỏi người ấy phải đi với vận tốc bao nhiêu để có thể gặp được ô tô?
6) Một cầu thang cuốn đưa hành khách từ tầng trệt lên tầng lầu trong siêu thị. Cầu thang trên đưa một người hành khách đứng yên lên lầu trong thời gian t1 = 1 phút. Nếu cầu thang không chuyển động thì người hành khách đó phải đi mất thời gian t2 = 3 phút. Hỏi nếu cầu thang chuyển động, đồng thời người khách đi trên nó thì phải mất bao lâu để đưa người đó lên lầu.
Gọi v1: vận tốc chuyển động của thang ; v2 : vận tốc người đi bộ.
*Nếu người đứng yên còn thang chuyển động thì chiều dài thang được tính:
	s = v1.t1 	
*Nếu thang đứng yên, còn người chuyển động trên mặt thang thì chiều dài thang được tính:
*Nếu thang chuyển động với vận tốc v1, đồng thời người đi bộ trên thang với vận tốc v2 thì chiều dài thang được tính:
Thay (1), (2) vào (3) ta được: 
7) Một người đi hết quãng đường AB dài 68 km, được chia làm hai đoạn: Đoạn đường đầu AC là đường nhựa, người đó đi với vận tốc 40km/h và đoạn đường còn lại BC là đường đất nên vận tốc chỉ đạt 24km/h. Biết thời gian đi từ A đến B là 2h, hãy tính độ dài đoạn đường nhựa và độ dài đoạn đường đất
Gọi quãng đường AC là x (km, x>0)
Thì quãng đường BC là 68-x
Thời gian đi hết quãng đường AC là: t1 = 
Thời gian đi hết quãng đường CB là: t2 = 
Theo bài ra ta có: t1 + t2 = 2 à + = 2
Giải phương trình ta được x = 50 km
Vậy quãng đường AC dài 50 km, quãng đường CB dài 18 km.
8) Trên một đường gấp khúc tại thành một tam giác đều ABC cạnh a = 30m, có hai xe khởi hành cùng lúc tại A. Xe (I) chuyển động theo hướng AB với vận tốc không đổi v1 = 3m/s; Xe (II) chuyển động theo hướng AC, với vận tốc không đổi v2 = 2m/s. Mỗi xe chạy 5 vòng.
 Hãy xác định số lần hai xe gặp nhau, vị trí vả thời điểm hai xe gặp nhau (không kể những lần hai xe gặp nhau ở A).
v1
v2
B
A
C
Ta có chu vi của đường ABC là: s = 3a = 3.30 = 90 (m).
 Hai xe gặp nhau khi tổng quãng đường đi từ đầu (hay lần gặp nhau trước đó) đúng bằng chu vi của tam giác.
Vậy khoảng thời gian giữa hai lần gặp nhau liên tiếp được tính bởi:
	v1t + v2t = S 
 Vậy chọn gốc thời gian là lúc khởi hành thì các thời điểm gặp nhau là:
	t1 = 1.18(s)
	t2 = 2.18 = 36(s)
	t3 = 3.18 = 54(s)
	..................................	
	tn = n.18 = 18n(s).
 Ngoài ra v1 > v2 nên với 5 vòng chạy thì xe (I) đi hết thời gian:
t = = 150(s).
Xe (I) tới A vào những thời điểm:
t'1 = 30s; t'2 = 60s; t'1 = 30s; t'3 = 90s; t'4 = 120s; t'5 = 150s.
Ta suy ra:
- Không kể những lần gặp nhau ở A thì hai xe gặp nhau trên đường đi ở các thời điểm:
t1 = 18s; t2 = 36s; t3 = 54s; t4 = 72s; t6 = 108s; t7 = 126s; t8 = 144s.
Có tất cả 7 lần gặp nhau trên đường đi.
- Vị trí gặp nhau được tính từ các thời điển trên và so với đỉnh gần nhất là:
Lần 1: Cách C đoạn CM1 = 6m theo chiều CB
Lần 2: Cách B đoạn BM2 = 12m theo chiều BA
Lần 2: Cách C đoạn CM3 = 6m theo chiều CA
Lần 4: Cách B đoạn BM4 = 6m theo chiều BC 
Lần 5: Cách C đoạn CM5 = 6m theo chiều CB 
(bỏ lần gặp ở A và do đó coi như hai xe lại chuyển động bắt đầu từ A).
Lần 6: Cách B đoạn BM6 = 12m theo chiều BA
Lần 7: Cách C đoạn CM7 = 12m theo chiều CA.
9) : Hai xe (I) và (II) chuyển động trên một đường tròn với vận tốc không đổi. Xe (I) đi hết 1 vòng mất 10phút, xe (II) đi 1 vòng 50phút.
 Hỏi khi xe (II) đi 1 vòng thì gặp xe (I) mấy lần, trong các trường hợp sau đây?
a. Hai xe khởi hành cùng lúc tại một điểm trên đường tròn và chuyển động cùng chiều.
b. Hai xe khởi hành cùng lúc tại một điểm trên đường tròn và chuyển động ngược chiều. 
a. Hai xe chuyển động cùng chiều:
 Theo đề ra ta suy ra:
Vận tốc xe (I) là: v1 = vòng/phút
Vận tốc xe (II) là: v2 = vòng/phút.
Đặt t là thời điểm hai xe gặp nhau. Quãng đường các xe đi được cho tới lúc đó là:
S1 = v1t = (vòng). S2 = v2t = (vòng).
 Ta phải có: S1 - S2 = n (vòng) (n4)
R
O
v1 v2
 = n = n t = = 12,5n (phút) (t50phút).
Các thời điểm gặp nhau là:
* n = 1 t1 = 12,5phút
	* n = 2 t2 = 25phút
	* n = 3 t3 = 37,5phút
	* n = 4 t4 = 50phút
 Vây khi chuyển động cùng chiều và khởi 
hành cùng lúc, tại một điểm thì xe (II) gặp
 xe (I) 4 lần cho mỗi vòng của nó.
b. Hai chuyển động ngược chiều:
Vận dụng các kết quả ở câu a. 
ta có điều kiện cho trường hợp này là: 
S1 + S2 = n(vòng) (n6) = n
 = n t = (phút) n (t50phút).
R
O
v1 v2
Các thời điểm gặp nhau là:
	* n = 1 t1 = 8,3phút
	* n = 2 t2 = 16,7phút
	* n = 3 t3 = 25phút
	* n = 4 t4 = 33,3hút
	* n = 5 t5 = 41,7phút
	* n = 6 t6 = 50phút
10) Một vật chuyển động trên hai đoạn đường với vận tốc trung bình v1, v2.
 Trong điều kiện nào vận tốc trên cả đoạn đường bằng trung bình cộng vủa các vận tốc?
Ta có: v = 
Trung bình cộng của hai vận tốc là: Vtb = 
Theo đề ra, ta có: 
2(v1t1 + v2t2) = (v1+v2)t1 + (v1+v2)t2
v1t1 + v2t2 = v1t2 + v2t1
v1t1 + v2t2 = v1t2 + v2t1
v1(t1+t2) + v2(t2- t1) = 0
Vì: v1 - v2 0, ta suy ra: t1 = t2.
Khoảng thời gian của hai chuyển động phải bằng nhau
11) : Hai xe khởi hành đồng thời từ A đi đến B theo chuyển động thẳng đều, A cách B một khoảng l.
 Xe (1) đi nửa đoạn đường đầu với vận tốc v1 và nửa đoạn đường sau đi với vận tốc v2.
Xe (2) đi nửa thời gian đầu với vận tốc v1 và nửa thời gian sau đi với vận tốc v2.
 Hỏi xe nào đi đển trước và đến trước bao lâu?(Xe 2 tới trước) .
12) Ba người đi xe đạp đều xuất phát từ A đi về B. Người thứ nhất đi với vận tốc
v1 = 8km/h. Sau 15phút thì người thứ hai xuất phát với vận tốc là v2=12km/h. Người thứ ba đi sau người thứ hai 30 phút. Sau khi gặp người thứ nhất, người thứ ba
đi thêm 30 phút nữa thì sẽ ở cách đều người thứ nhất và người thứ hai. 
Tìm vận tốc của người thứ ba. 
Khi người thứ ba xuất phát thì người thứ nhất đã đi được quãng đường là
 S1 =v1.t1 = 8. 0,75 =6km
Người thứ hai đã đi được quãng đường là
 S2 =v2.t2 = 12.0,5 =6km
Gọi t là thời gian người thứ ba đi đến gặp ngườ thứ nhất 
 v3. t = s1 + v1. t => t= (1)
Sau t’=t + 0,5 hthì 
Quãng đường người thứ nhất đi được là
 l1 = s1 + v1. t’ = 6 + 8(t + 0,5)
Quãng đường người thứ hai đi được là
 L2 = s2 + v2. t’ = 6 + 12(t + 0,5)
Quãng đường người thứ ba đi được là
 L3 = v3. t’ = v3 . (t + 0,5)
Theo dề bài ta có l2- l3 = l3- l1 => l2+l1 = 2 l3 
 6 + 8(t + 0,5)+ 6 + 12(t + 0,5) =2 v3 . (t + 0,5)
12 = ( 2v3 - 20) . (t + 0,5) (2)
Thay (1) vào (2) ta có phương trình
 v32 -18 . v3 + 56 =0
 Hai nghiệm của phương trình là 
 v3= 4km/h (Loại vì v3 <v1 ,v2)
 v3= 14km/h 
11) Người ta rải đều bột của một chất dễ cháy thành một dải hẹp dọc theo một đoạn thẳng từ A đến B và đồng thời châm lửa đốt từ hai vị trí D1, D2. Vị trí thứ nhất D1 cách A một đoạn bằng 1/10 chiều dài của đoạn AB, vị trí thứ hai D2 nằm giữa D1B và cách vị trí thứ nhất một đoạn Do có gió thổi theo chiều từ A đến B nên tốc độ cháy lan của ngọn lửa theo chiều gió nhanh gấp 7 lần theo chiều ngược lại. Toàn bộ dải bột sẽ bị cháy hết trong thời gian t1=60 giây. Nếu tăng lên gấp đôi giá trị ban đầu thì thời gian cháy hết là t2=61 giây. Nếu giảm xuống còn một nửa giá trị ban đầu thì thời gian cháy hết là t3=60 giây. Tính chiều dài của đoạn AB.
12) Hai ô tô chuyển động thẳng đều từ hai địa điểm A và B cách nhau 20 km. Xe chuyển động từ A với vận tốc v1 = 30 km/h, xuất phát lúc 7 giờ và đi theo chiều từ A đến B. Xe chuyển động từ B với vận tốc v2 = 40km/h, xuất phát lúc 8 giờ và đi cùng chiều với xe chuyển động từ A.
a) Xác định vị trí gặp nhau của hai xe.
b) Xác định khoảng cách giữa 2 xe sau 3 giờ, tính từ lúc xe A bắt đầu chuyển
- Chọn gốc toạ độ tại vị trí A
- Chọn gốc thời gian lúc 7h
	- Chọn chiều dương là chiều từ A đến B 
+ Phương trình chuyển động của xe xuất phát từ A:
 (1)
+ Phương trình chuyển động của xe xuất phát từ B:
 (2)
a) Vị trí gặp nhau của hai xe.
	- Khi hai xe gặp nhau: 
	Vậy hai xe gặp nhau tại vị trí: .
b) Khoảng cách hai xe sau 3h là :
Sau 3h toạ độ của các xe lần lượt là: ; 
Ta được: .
13) ): Các đường biểu diễn (I) và (II) trên hình 1 biểu diễn chuyển động thẳng đều của xe 1 và xe 2 theo cùng một chiều. Dựa vào đồ thị, hãy cho biết:
	a. Địa điểm, thời điểm xuất phát của mỗi xe.
	b. Vận tốc chuyển động của mỗi xe.
	c. Khoảng cách giữa hai xe lúc 4h15 phút.
a. 
Địa điểm:
Xe 1 xuất phát tại điểm cách gốc tọa độ 40 km. 
Xe 2 xuất phát tại gốc tọa độ.
Thời điểm:
Xe 1 xuất phát lúc 0 h.
Xe 2 xuất phát lúc 1 h. 
b. 
Xe 1 đi được quãng đường s1= 70 km trong t1= 7 giờ à vận tốc xe 1 là v1= s1/t1 = 10 (km/h). 
Xe 2 đi được quãng đường s2 = 120 km trong t2 = 6 h à vận tốc xe 2 là v2= s2/t2 = 20 (km/h
c. 
Thời gian 2 xe đã đi tính tới thời điểm 4h15’ là t1 = 4 h15’ = 4,25h và t2 = 3h15’ = 3,25h
Quãng đường 2 xe đi được trong thời gian đó là s1 = v1.t1 = 10.4,25 = 42,5 (km) và s2 = v2.t2 = 20.3,25 = 65 (km)
Vì xe 1 xuất phát cách gốc tọa độ 40 km và xe 2 xuất phát tại gốc tọa độ nên tại thời điểm 4h15’ hai xe cách gốc tọa độ những khoảng x1 = 40 + 42,5 = 82,5 km và x2 = 65 km à Khoảng cách hai xe Dx = x1 – x2 = 17,5 km
 13) Hải, Quang và Tùng cùng khởi hành từ A lúc 8 giờ để đi đến B, với AB = 8 km. Do chỉ có một xe đạp nên Hải chở Quang đến B với vận tốc v1 = 16 km/h, rồi liền quay lại đón Tùng. Trong lúc đó Tùng đi bộ dần đến B với vận tốc v2 = 4 km/h.
	 a, Hỏi Tùng đến B lúc mấy giờ ? Quãng đường Tùng phải đi bộ là bao nhiêu km ?
	 b, Để Hải đến B đúng 9 giờ, Hải bỏ Quang tại một điểm nào đó rồi lập tức quay lại chở Tùng cùng về B, Quang tiếp tục đi bộ về B. Tìm quãng đường đi bộ của Tùng và của Quang. Quang đến B lúc mấy giờ ? 
 Biết xe đạp luôn chuyển động đều với vận tốc v1, những người đi bộ luôn đi với vận tốc v2
a, (1,5 đ)
- Gọi C là điểm gặp nhau của Hải và Tùng.
- Trong cùng khoảng thời gian t1 : Hải đi xe đạp đoạn đường s + s1 và Tùng A
.
s
.
.
C
B
s3
s1
đi bộ quãng đường s3.
Ta có: s + s1 = v1.t1 ; s3 = v2.t1 ; s1 + s3 = s
 s + s1 + s3 = v1.t1 + s3 2s = v1.t1 + v2.t1 
 t1 = 0,8 (h)
- Sau đó từ C, Hải và Tùng cùng về B với vận tốc v1 trong thời gian t2 :
 t2 = = = 0,3 (h) 
- Thời gian tổng cộng của Tùng đi là : t = t1 + t2 = 0,8 + 0,3 = 1,1(h) = 1 giờ 6 phút.
- Vậy Tùng đến B lúc 9 giờ 6 phút và quãng đường Tùng đi bộ là :
 s3 = v2.t1 = 4.0,8 = 3,2 (km).
 ---------------------------------------------------------------------------------------------------
A
.
.
.
E
B
D
.
s1
s3
s2
s
b, (1,0 đ)
Gọi t1 là thời gian Hải đi xe đạp chở Quang từ A đến D rồi quay về E, cũng là thời gian Tùng đi bộ từ A đến E (AE = s3). 
 s3 = v2.t1 (1)
-Sau đó Hải và Tùng cùng đi xe đạp từ E đến B (EB = s1) trong khoảng thời gian t2.
 Ta có : s1 = v1.t2 (2)
 t1 + t2 = 9 – 8 = 1 (h) (3)
 s3 + s1 = 8 (km) (4)
Từ (1), (2), (3) và (4), giải ra ta có: t1 = (h) 
- Quãng đường đi bộ của Tùng là : s3 = v2.t1 = ≈ 2,67 (km) 
- Ta cũng có : AD + DE = v1.t1 (5)
- Từ (1) và (5) => AD + DE + AE = 2AD = v1.t1 + v2.t1 = t1(v1 + v2)
 => AD = t1(v1+v2)2 = 23.(16+4)2 = 203 (km)
- Quãng đường đi bộ của Quang : DB = s2 = AB – AD = 8 - 203 = 43 ≈ 1,33 (km)
- Tổng thời gian Quang đi từ A B là : t3 = ADv1 + s2v2 = 20316 + 434 = 34 (h) = 45 ph Vậy Quang đến B lúc 8 giờ 45 phút.
13) Một tàu hỏa chiều dài L =150 m đang chạy với vận tốc không đổi v = 10 m/s trên đường ray thẳng, song song và gần đường quốc lộ 1A. Một xe máy và một xe đạp đang chạy thẳng trên đường 1A, ngược chiều nhau, tốc độ không đổi lần lượt là v1 và v2. Tại thời điểm t0 = 0, xe máy bắt đầu đuổi kịp tàu, còn xe đạp bắt đầu gặp tàu (hình 1).
a) Xe máy bắt đầu vượt qua tàu sau khi xe máy đã đi được quãng đường kể từ thời điểm t0 = 0, hãy tính tốc độ v1 của xe máy.
b) Xe máy và xe đạp gặp nhau tại vị trí cách đầu tàu một khoảng hãy tính tốc độ v2 của xe đạp.
v1
Xe máy
Xe đạp
Tàu hỏa
v2
v
Hình 1
a) (1 điểm)
Quãng đường tàu hỏa đi được đến khi xe máy vượt qua là s1 - L
Thời gian xe máy đi quãng đường s1 bằng thời gian tàu đi quãng đường s1 - L
 ......................................................................................................................................................................................................................................................................
® v1 = = 16 m/s 
b) (1 điểm)
Thời điểm xe máy và xe đạp gặp nhau
t1 = ...................................................................................................................................................................................................................................................................
Khoảng cách từ vị trí gặp nhau đến đầu tàu
l = vt1 + v2t1 = (v + v2) 
® v2 = = = 4 m/s