Giải bộ đề thi học sinh giỏi Toán lớp 10 (năm 2015) - Trường THPT chuyên cao bằng

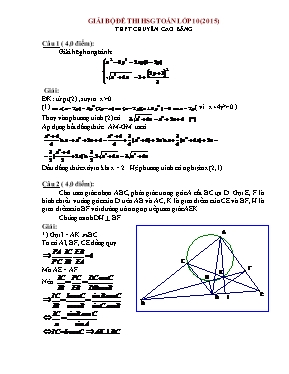
GIẢI BỘ ĐỀ THI HSG TOÁN LỚP 10 (2015)
 THPT CHUYấN CAO BẰNG
Cõu 1 ( 4,0 điểm ): 
Giải hệ phơng trình:
 Giải:
ĐK: từ pt (2) ,suy ra x> 0
(1)( vỡ x+4y2> 0 )
Thay vào phương trỡnh (2) cú 
Ap dụng bất dẳng thức AM-GM tacú 
Dấu đẳng thức xảy ra khi x = 2. Hệ phương trỡnh cú nghiệm x(2,1)
Cõu 2 ( 4,0 điểm ): 
Cho tam giỏc nhọn ABC, phõn giỏc trong gúc A cắt BC tại D. Gọi E, F là hỡnh chiếu vuụng gúc của D trờn AB và AC, K là giao điểm của CE và BF, H là giao điểm của BF với đường trũn ngoại tiếp tam giỏc AEK. 
Chứng minh DH ^ BF.
Giải:
*) Gọi I = AK BC
Ta cú AI, BF, CE đồng quy
Mà AE = AF
Nờn 
*) A, E, H, K cựng thuộc một đường trũn 
 A, E, D, I cựng thuộc một đường trũn 
 HKID nội tiếp.
Mà gúc DIK vuụng nờn gúc DHK vuụng. ố Vậy DH BF (ĐPCM)
Cõu 3 ( 4,0 điểm): 
Cho thỏa món . Chứng minh rằng
Giải:
Áp dụng BĐT Bunhiakopxki ta được
Lại cú 
Suy ra: (*)
Ta sẽ chứng minh (1)
Đặt 
Từ giả thiết suy ra . 
Vậy (2)
Nếu .
Nếu . Ta cú (vỡ ). Suy ra (vỡ ). 
Vậy: . Từ (*) suy ra 
Cõu 4 ( 4,0 điểm):
Tỡm tất cả cỏc bộ ba số tự nhiờn lớn hơn 1 sao cho tớch của hai số bất kỳ cộng 1 chia hết cho số cũn lại.
Giải:
Gọi a, b, c là ba số tự nhiờn lớn hơn 1 thỏa món điều kiện
Dễ thấy a, b, c là ba số đụi một nguyờn tố cựng nhau ( vỡ nếu cú hai số khụng nguyờn tố cựng nhau chẳng hạn a và b thỡ ( a, b) >1. Khi đú (ac, b) = d >1 
à suy ra ac +1 khụng chia hết cho d , do đú ac + 1 cũng khụng chia hết cho b ), 
à suy ra cỏc số đú là khỏc nhau.
Số S = ab + bc + ca + 1 chia hết cho cỏc số a, b, c nờn S chia hết cho abc 
( vỡ cỏc số a, b, c là ba số đụi một nguyờn tố cựng nhau). Vỡ vậy .
* Khụng mất tớnh tổng quỏt, giả sử 2Ê a Ê b Ê c.
 Nếu , khi đú , và 
.
Điều mõu thuẫn này chứng tỏ , do đú . Vỡ chia hết cho 7 nờn .
Vậy bài toỏn chỉ cú một bộ ba số duy nhất thỏa món điều kiện là 2, 3, 7.
Cõu 5 (4,0 điểm) 
Cho 2015 tập hợp, mỗi tập hợp cú 45 phần tử và hai tập bất kỡ cú đỳng một phần tử chung. Chứng minh rằng tồn tại một phần tử thuộc tất cả 2015 tập hợp trờn.
H D Giải:
Xột tập A trong số 2015 tập đó cho. A giao với 2014 tập cũn lại nờn tồn tại là phần tử chung của khụng ớt hơn tập cũn lại.
Vậy a thuộc cỏc tập và trong 46 tập này khụng cú hai tập nào cú phần tử chung khỏc a.
Ta sẽ chứng minh a thuộc tập B bất kỡ trong 20105 tập đó cho.
Thật vậy, nếu thỡ B cú với mỗi tập một phần tử chung khỏc a, suy ra B cú khụng ớt hơn 46 phần tử, mõu thuẫn. Bài toỏn được chứng minh.
 PHH sưu tầm & GT - 12/2015 - nguồn THPT chuyờn Cao Bằng