Đề thi trung học phổ thông quốc gia bài thi môn: Toán

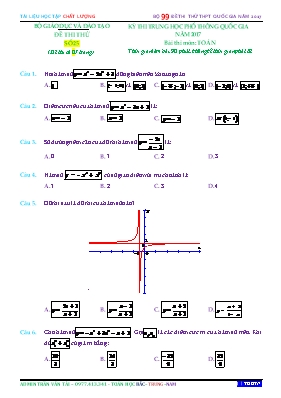
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ
SỐ 25
(Đề thi có 07 trang)
KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2017
Bài thi môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Hỏi hàm số đồng biến trên khoảng nào
A. 	B. và 	C. và 	D. và 
Điểm cực tiểu của hàm số là:
A. 	B. 	C. 	D. 
Số đường tiệm cận của đồ thị hàm số là:
A. 0	B. 1	C. 2	D. 3
Hàm số có số giao điểm với trục hoành là:
A. 1	B. 2	C. 3	D. 4
Đồ thị sau là đồ thị của hàm số nào? 
`
A. 	B. 	C. 	D. 
Cho hàm số. Gọi là các điểm cực trị của hàm số trên. Khi đó có giá trị bằng :
A. 	B. 	C. 	D. 
Cho hàm số . Giá trị của tham số để tiệm cận đứng của đồ thị hàm số đã cho đi qua điểmlà
A. 	B. 	C. 	D. 
Giá trị lớn nhất của hàm số trên là:
A. 	B. 	C. 	D. 
Giá trị của tham số để hàm số luôn nghịch biến trênlà:
A. 	B. 	C. 	D. 
Giá trị của tham số để đồ thị hàm sốcắt trục hoành tại 3 điểm phân biệt là:
A. 	B. 	C. 	D. 
Cho hai vị trí , cách nhau , cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách từ và từ đến bờ sông lần lượt là và Một người đi từ đến bờ sông để lấy nước mang về . Đoạn đường ngắn nhất mà người đó có thể đi là:
A. 	B. 	C. 	D. 
Biểu thứccó giá trị bằng:
A. 12	B. 16	C. 3	D. 9
Đạo hàm của hàm sốlà:
A. 	B. 
C. 	D. 
Phương trình có số nghiệm là:
A. 0	B. 1	C. 2	D. 3
Giá trị của bằng:
A. 	B. 	C. 	D. 
Hàm số 
A. có một cực tiểu.	B. không có cực trị.
C. có một cực đại.	D. có một cực đại và một cực tiểu.
Phương trình có bao nhiêu nghiệm thực phân biệt?
A. 2.	B. 3.	C. 4.	D. 1.
Cho số thực thỏa mãn ; . Khi đó là:
A. 	B. 	C. 	D. 
Tập xác định của hàm sốlà:
A. 	B. 
C. 	D. 
Phương trình có hai nghiệm phân biệt khi:
A. 	B. 	C. 	D. 
Người ta thả một ít lá bèo vào hồ nước. Biết rằng sau 1 ngày, bèo sẽ sinh sôi kín cả mặt hồ và sau mỗi giờ lượng lá bèo tăng gấp 10 so với trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì lá bèo phủ kín mặt hồ?
A.	B.	C. 	D. 
Một ca nô đang chạy trên hồ Tây với vận tốc thì hết xăng; từ thời điểm đó, ca nô chuyển động chậm dần đều với vận tốc , trong đó là khoảng thời gian tính bằng giây, kể từ lúc hết xăng. Hỏi từ lúc hết xăng đến lúc ca nô dừng hẳn đi được bao nhiêu mét?
A. 10m 	B. 20m 	C. 30m 	 D. 40m
Tíchphân bằng:
A. 	B. 	C. 	D. 
Tíchphân bằng
A. .	B. .	C. .	D. 
Thể tích của vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi các đường quanh trục hoành có giá trị bằng?
A. 	B. 	C. 	D. 
Giá trị để hàm số là một nguyên hàm của hàm số là
A. 	B. 	C. 	D. 
Tíchphân bằng:
A. 	B. 	C. 	D. 
Trong Giải tích, với hàm số liên tục trên miền có đồ thị là một đường cong thì độ dài củađược xác định bằng công thức Với thông tin đó, hãy tính độ dài của đường cong cho bởi trên là:
A. 	B. 	C. 	D. 
Phần thực và phần ảo của số phức là:
A. phầnthực là 1, phầnảo là 	B. phầnthực là 1, phầnảo là -1.
C. phầnthực là 1, phầnảo là 1.	D. phầnthực là 1, phầnảo là -.
Số phức liên hợp của số phứclà :
A. 	B. 	C. 	D. 
Cho số phức thỏa mãn . Khi đó tọa độ điểm biểu diễn của là:
A. 	B. 	C. 	D. 
Cho haisốphứcGiátrịcủabiểuthứclà:
A. 	B. 	C. 	D. 
Gọi là hai nghiệm phức của phương trình Giá trị biểu thức là
A. 15	B. 17	C. 19	D. 20
Tập hợp các điểm biểu diễn số phức thỏa mãn trên mặt phẳng tọa độ là một
A. Đường thẳng	B. Đường tròn	C. Elip	D. Hypebol
Khối đa diện đều loại là khối đa diện có?
A. cạnh, mặt	B. mặt, cạnh	C. mặt, đỉnh	D. đỉnh, cạnh
Cho hình chóp có đáy là tam giác vuông tại vớicạnhvuông góc với và. Thể tích khối chóp là
A. 	B. 	C. 	D. 
Cho hình chóp có đáy là hình vuông cạnh tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp là:
A. 	B. 	C. 	D. 
Cho tứ diện có vuông góc với mặt phẳng , . Khoảng cách từ đến mặt phẳng là
A.	B. 	C. 	D. 
Gọi là bán kính đường tròn đáy và là độ dài đường sinh của một hình nón. Diện tích xung quanh của hình nón là:
A. 	B. 	C. 	D. 
Một hình trụ có bán kính đáy có thiết diện qua trục là một hình vuông. Diện tích xung quanh bằng:
A. 	B. 	C. 	D. 
Một hình cầu có thể tích ngoại tiếp một hình lập phương. Thể tích của khối lập phương là:
A. 	B. 	C. 1	D. 
Cho hình lăng trụ tam giác đều có các cạnh đều bằng Thể tích khối cầu ngoại tiếp hình lăng trụ đó là:
A. 	B. 	C. 	D. 
Mặt cầu có bán kính là
A. 	B. 	C. 	D. 
Vectơ pháp tuyển của mặt phẳng là:
A. 	B. 	C. 	D. 
Trong không gian với hệ trục tọa độ cho là mặt cầu tâm và tiếp xúc với mặt phẳng . Khi đó, bán kính của là:
A. 	B. 2	C. 3	D. 
Trong không gian với hệ trục tọa độ tọa độ giao điểm của đường thẳng và mặt phẳng là
A. 	B. 	C. 	D. 
Trong không gian với hệ trục tọa độ cho hai điểm và mặt phẳng Gọi là điểm trên để tam giác đều tọa độ điểm là: 
A. 	B.	C. 	D. 
Trong không gian với hệ trục tọa độ cho hai mặt phẳngvàHai mặt phẳngvàvuông góc với nhau khi:
A. 	B. 	C. 	D. 
Trong không gian với hệ trục tọa độ chovàVectơ chỉ phương của đường thẳng là giao tuyến của và mặt phẳng trung trực của là:
A. 	B. 	C. 	D. 
Trong không gian với hệ trục tọađộ cho hai điểmvà mặt phẳngNếu thay đổi thuộc thì giá trị nhỏ nhất củalà
A. 60	B. 50	C. 	D. 
---------------------------------------------------------- HẾT ----------
BẢNG ĐÁP ÁN
Câu 1
D
Câu 11
C
Câu 21
B
Câu 31
A
Câu 41
A
Câu 2
B
Câu 12
D
Câu 22
D
Câu 32
B
Câu 42
A
Câu 3
C
Câu 13
C
Câu 23
B
Câu 33
D
Câu 43
D
Câu 4
C
Câu 14
B
Câu 24
D
Câu 34
C
Câu 44
A
Câu 5
A
Câu 15
B
Câu 25
A
Câu 35
A
Câu 45
B
Câu 6
A
Câu 16
C
Câu 26
C
Câu 36
D
Câu 46
B
Câu 7
A
Câu 17
C
Câu 27
B
Câu 37
C
Câu 47
D
Câu 8
D
Câu 18
B
Câu 28
C
Câu 38
A
Câu 48
A
Câu 9
C
Câu 19
C
Câu 29
C
Câu 39
A
Câu 49
D
Câu 10
A
Câu 20
A
Câu 30
C
Câu 40
B
Câu 50
A
HƯỚNG DẪN GIẢI CÁC CÂU KHÓ
Câu 11. 
Giả sử người đó đi từ A đến M để lấy nước và đi từ M về B.
dễ dàng tính được Ta đặt khi đó ta được:
Như vậy ta có hàm số được xác định bằng tổng quãng đường AM và MB:
 với 
Ta cần tìm giá trị nhỏ nhất của để có được quãng đường ngắn nhất và từ đó xác định được vị trí điểm M. 
Hàm số liên tục trên đoạn . So sánh các giá trị của , , ta có giá trị nhỏ nhất là 
Khi đó quãng đường đi ngắn nhất là xấp xỉ 779,8m. Vậy đáp án là C.
Câu 21.
Gọilà thời gian các lá bèo phủ kíncái hồ.Vì tốc độ tăng không đổi, 1 giờ tăng gấp 10 lần nên ta có.
Câu 22. Khi ca nô dừng thì 
Khi đó quảng đường đi được từ khi hết xăng là
Ta có .
Câu 28. 
Ta cónên áp dụng công thức đã cho sẽ được
với
Do đó.
Câu 42.Ta cóSuy ra
Câu 50. 
Ta cóvớilà trung điểm của
Câu chuyện con Lừa và bài học cuộc sống
Một ngày nọ, con lừa của một ông chủ trang trại sảy chân rơi xuống một cái giếng. Lừa kêu la tội nghiệp hàng giờ liền. Người chủ trang trại cố nghĩ xem nên làm gì. Cuối cùng ông quyết định: con lừa đã già, dù sao thì cái giếng cũng cần được lấp lại và không ích lợi gì trong việc cứu con lừa lên cả.
Ông nhờ vài người hàng xóm sang giúp mình. Họ xúc đất và đổ vào giếng. Ngay từ đầu, lừa đã hiểu chuyện gì đang xảy ra và nó kêu la thảm thiết. Nhưng sau đó lừa trở nên im lặng. Sau một vài xẻng đất, ông chủ trang trại nhìn xuống giếng và vô cùng sửng sốt. Mỗi khi bị một xẻng đất đổ lên lưng, lừa lắc mình cho đất rơi xuống và bước chân lên trên. Cứ như vậy, đất đổ xuống, lừa lại bước lên cao hơn. Chỉ một lúc sau mọi người nhìn thấy chú lừa xuất hiện trên miệng giếng và lóc cóc chạy ra ngoài.
Cuộc sống sẽ đổ rất nhiều thứ khó chịu lên người bạn. Hãy xem mỗi vấn đề bạn gặp phải là một hòn đá để bạn bước lên cao hơn.
Chúng ta đừng bao giờ đầu hàng.
GIÁO VIÊN HOẶC TỔ CHỨC CẦN FILE WORD ĐỂ SOẠN – LIÊN HỆ THẦY TRẦN TÀI
SĐT: 0977.413.341 – MAIL: trantai.gvt@gmail.com – CHÚC NĂM HỌC THÀNH CÔNG !
CHỈ 10K / ĐỀ CHẤT LƯỢNG – CHUNG TAY CÙNG PHÁT TRIỂN