Đề thi thử THPTQG lần I năm 2017 môn Toán lớp 11

TRƯỜNG THPT A
Tổ Toán Tin
ĐỀ THI THỬ THPTQG LẦN I NĂM 2017
MÔN TOÁN LỚP 11
Thời gian làm bài: 90 phút
Phần 1: Trắc nghiệm
Câu 1: Tập xác định D của hàm số là
A. R	B. 	C. 	D. 
Câu 2: Chu kỳ của hàm số là:
A. 	B. 	C. 	D. 
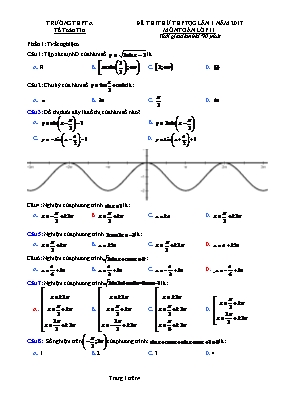
Câu 3: Đồ thị dưới đây là đồ thị của hàm số nào?
A. 	B. 
C. 	D. 
Câu 4: Nghiệm của phương trình là:
A. 	B. 	C. 	D. 
Câu 5: Nghiệm của phương trình là:
A. 	B. 	C. 	D. 
Câu 6: Nghiệm của phương trình:
A. 	B. 	C. 	D. `
Câu 7: Nghiệm của phương trình là: 
A. 	B. 	C. 	D. 
Câu 8: Số nghiệm trên của phương trình: là:
A. 1	B. 2	C. 3	D. 4
Câu 9: Hằng ngày, mực nước của một con kênh lên xuống theo thủy triểu. Độ sau h (m) của con kênh tính theo thời gian t (giờ) trong một ngày được cho bởi công thức: . Thời điểm mực nước của kênh cao nhất là:
A. t = 16
B. t = 15
C. t = 14
D. t = 13
Câu 10: Lớp 11B có 40 học sinh bao gồm15 học sinh nam và 25 học sinh nữ. Giáo viên chủ nhiệm cần chọn ra 3 bạn học sinh để làm lớp trưởng, lớp phó và bí thư. Số cách chọn ra 3 bạn đó là:
A.117
B.9880
C.59280
D.69280
Câu 11: Nghiệm của bất phương trình:	là: 
A. 
B. 
C. 
D. 
Câu 12: Cho tập X = {0,1,2,3,4,5,6,7}. Có thể lập được bao nhiêu số tự nhiên chẵn gồm 5 chữ số khác nhau đôi một từ X?
A. 3660 
B. 3000
C. 2880
D. 2160
Câu 13: Hệ số x10 trong khai triển là: 
A.2
B.495
C.12
D.66
Câu 14: Tổng tất cả các hệ số trong khai triển 
A.2
B. 
C.1
D. -
Câu 15: Gieo hai đồng xu cân đối đồng chất cùng một lúc. Xác suất để được hai mặt giống nhau là:
A. 
B. 
C. 
D. 
Câu 16: Chọn ngẫu nhiên 2 người đi công tác từ một tiểu đội gồm 4 hạ sĩ và 6 binh nhất. Xác suất để 2 người được chọn có cùng cấp bậc là: 
A. 
B. 
C. 
D. 
Câu 17: Có hai hộp đựng bi. Hộp thứ nhất có 9 viên bi được đánh số từ 1 đến 9. Lấy ngẫu nhiên mỗi hộp một viên bi. Biết rằng xác suất lấy được viên bi mang số chẵn ở hộp thứ 2 là . Xác suất để lấy được cả hai viên bi mang số chẵn là:
A. 
B. 
C. 
D. 
Câu 18: Đội tuyển học sinh giỏi thể dục thể thao trường THPT Kim Sơn A gồm 10 học sinh khối 10, 15 học sinh khối 11 và 12 học sinh khối 12. Chọn ngẫu nhiên 7 em đi nhận phần thưởng do Tỉnh đoàn phát trưởng. Xác suất để trong số 7 em được chọn có ít nhất một học sinh khối 12 là:
A. 
B. 
C. 
D. 
Câu 19. Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + y – 3 = 0. Hỏi phép vị tự tâm O tỉ số k = 2 biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?
A. . 2x + 2y = 0                                    
B. 2x + y – 6 = 0
C. 4x – 2y – 3 = 0                                                
D. x + y – 4 = 0
Câu 20: Trong mặt phẳng Oxy, cho và đường tròn . Gọi là ảnh của qua phép tịnh tiến , là ảnh của qua phép quay . Phương trình đường tròn là: 
A. 
B. 
C. 
D. 
Câu 21: Tính tổng . Khi đó công thức tổng quát của S(n) là:
 B. C. D. 
Câu 22: Một cấp số cộng có u5 = 7 và u10= 42 , công sai d của cấp số cộng này là : 
A.7 
B. -21
C. 3
D. 10
Câu 23: Cho CSN có . Số 192 là số hạng thứ:
A.5
B. 6
C. 7
D. Đáp án khác
Câu 24: Ba số a, b, c theo thứ tự lập thành một cấp số nhân với công bội q khác 1. Đồng thời các số a, 2b, 3c theo thứ tự lập thành một cấp số cộng với công sai d khác 0. Khi đó công bội q là:
A. 
B. 
C. 
D. -3
Câu 25: : Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DA, AC và BD. Trong các mệnh đề sau mệnh đề nào đúng?
	A. Hai đường thẳng RS và PQ cắt nhau.
	B. Hai đường thẳng NR và PQ cắt nhau.
	C. Hai đường thẳng MN và PQ song song với nhau.
	D. Hai đường thẳng RS và MP chéo nhau.
Câu 26: Cho tứ diện ABCD. Gọi I, J và K lần lượt là trung điểm của AC, BC và BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là:
A. KD	
B. Đường thẳng qua K và song song với AB	
C. KI
D. Không có
Câu 27: Cho tứ diện ABCD và ba điểm I, J, K lần lượt nằm trên các cạnh AB, BC, CD mà không trùng với các đỉnh. Thiết diện của hình tứ tiện ABCD khi cắt bởi mặt phẳng (IJK) là:
A. Một tam giác
B. Một tứ giác
C. Một hình thang
D. Một ngũ giác
Câu 28: Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và AC, E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là:
	A. Tam giác MNE	
	B. Tứ giác MNEF với F là điểm bất kì trên cạnh BD	
	C. Hình bình hành MNEF với F là điểm bất kì trên cạnh BD mà EF // BC	
	D. Hình thang MNEF với F là điểm trên cạnh BD mà EF // BC
Câu29: Cho tứ diện đều SABC cạnh bằng a. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng (a) song song với (SIC). Thiết diện tạo bởi (a) và tứ diện SABC là:
	A. Tam giác cân tại M	B. Tam giác đều
	C. Hình bình hành 	D. Hình thoi 
Câu 30: Cho tứ diện đều SABC cạnh bằng a. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng (a) song song với (SIC). Chu vi của thiết diện tạo bởi (a) và tứ diện SABC tính theo AM = x là:
	A. 	B. 	C. 3	D. Không tính được 
Câu 31: Ký hiệu M, m lần lượt là GTLN, GTNN của hàm số . Khi đó giá trị của M và m là: 
Câu 32: Các nghiệm của phương trình thuộc đoạn là
Câu 33: Phương trình có nghiệm khi m thỏa mãn: ..
Câu 34: Một bộ ghép hình gồm các miếng gỗ. Mỗi miếng gỗ được đặc trưng bởi 4 tiêu chuẩn: chất liệu, màu sắc, hình dạng và kích cỡ. Biết rằng có 2 chất liệu: nhựa và gỗ; có 4 màu: xanh, đỏ, lam, vàng; có 4 hình dạng: tròn, vuông, tam giác, lục giác và có 3 kích cỡ: nhỏ, vừa, lớn. Và không có miếng gỗ nào thiết kế giống nhau. Xét miếng gỗ “Nhựa, màu đỏ, hình tròn, vừa”. Số miếng gỗ khác miếng gỗ trên đúng 2 tiêu chuẩn là: ..
Câu 35: Đội học sinh giỏi cấp trường môn Tiếng Anh của trường THPT X theo từng khối như sau: khối 10 có 5 học sinh, khối 11 có 5 học sinh và khối 12 có 5 học sinh. Nhà trường cần chọn một đội tuyển gồm 10 học sinh tham gia IOE cấp tỉnh. Số cách lập đội tuyển sao cho có học sinh cả ba khối và có nhiều nhất 2 học sinh khối 10 là: ..
Câu 36: Mét hép ®ùng 11 tÊm thÎ ®­îc ®¸nh sè tõ 1 ®Õn 11. Chän ngÉu nhiªn 6 tÊm thÎ. Gäi P lµ x¸c suÊt ®Ó tæng sè ghi trªn 6 tÊm thÎ Êy lµ mét sè lÎ. Khi ®ã P =
Câu 37: Bèn quyÓn s¸ch ®­îc ®¸nh dÊu b»ng nh÷ng ch÷ c¸i: U, V, X, Y ®­îc xÕp tuú ý trªn mét kÖ s¸ch dµi. X¸c suÊt ®Ó chóng ®­îc xÕp theo thø tù b¶ng ch÷ c¸i lµ: .
Câu 38: Các giá trị của x để là ba số hạng liên tiếp của một cấp số cộng là :
..
Câu 39: Cho cấp số nhân (un) biết . Giá trị u1 và q là: .
Câu 40: Nghiệm của phương trình là : 
II. Phần 2: Tự luận: 
Bài 1:
Giải phương trình: 
Tìm hệ số của số hạng chứa trong khai triển biết 
 Một tổ có 12 học sinh gồm 8 nam và 4 nữ. Chọn một nhóm lao động gồm 6 học sinh. Tính xác suất để có 4 nam và 2 nữ được chọn.
Cho một cấp số cộng có u2 + u5 = 42 và u4 + u9 = 66. Hãy tính tổng 346 số hạng đầu tiên của cấp số cộng đó.
Bài 2: Cho hình chóp S.ABC. Gọi G là trọng tâm tam giác ABC; M, N trên cạnh SA sao cho SM = MN = NA.
Chứng minh rằng GM // (SBC)
LẤy điểm D đối xứng với A qua G. Chứng minh rằng: (MCD) // (NBG)
Gọi H là giao của MD và (SBC). Chứng minh rằng H là trọng tâm tam giác SBC 
=================Hết=================