Đề thi thử THPT quốc gia Toán 2017 - Trường THPT Thịnh Long

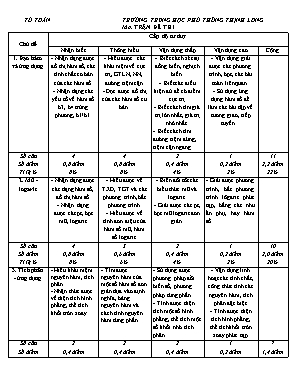
MA TRẬN ĐỀ THI
Chủ đề
Cấp độ tư duy
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Cộng
1. Đạo hàm và ứng dụng
- Nhận dạng được đồ thị hàm số, các tính chất cơ bản của các hàm số.
- Nhận dạng các yếu tố về hàm số b3, b4 trùng phương, b1/b1.
- Hiểu được các khái niệm về cực trị, GTLN, NN, đường tiệm cận. 
- Đọc được đồ thị của các hàm số cư bản.
- Biết cách xét sự đồng biến, nghịch biến.
- Biết các điều kiện đủ để có điểm cực trị.
- Biết cách tìm giá trị lớn nhất, giá trị nhỏ nhất.
- Biết cách tìm đường tiệm đứng, tiệm cận ngang.
- Vận dụng giải được các phương trình, bpt, các bài toán liên quan.
- Sử dụng ứng dụng hàm số để làm các bài tập về tương giao, tiếp tuyến ...
Số câu
Số điểm Tỉ lệ %
4
0,8 điểm
8%
4
0,8 điểm
8%
2
0,4 điểm
4%
1
0,2 điểm
2%
11
2,2 điểm
22%
2. Mũ - logarit
- Nhận dạng được các dạng hàm số, đồ thị hàm số.
- Nhận dạng được các pt, bpt mũ, logarit.
- Hiểu được về TXĐ, TGT và các phương trình, bất phương trình.
- Hiểu được về tính đơn điệu của hàm số mũ, hàm số logarit.
- Biến đổi tốt các biểu thức mũ và logarit.
- Giải được các pt, bpt mũ logarit đơn giản.
- Giải được phương trình, bất phương trình lôgarit phức tạp, bằng các như ẩn phụ, hay hàm số.
Số câu
Số điểm Tỉ lệ %
4
0,8 điểm
8%
3
0,6 điểm
6%
2
0,4 điểm
4%
1
0,2 điểm
2%
10
2,0 điểm
20%
3. Tích phân - ứng dụng
- Hiểu khái niệm nguyên hàm, tích phân.
- Nhận thức được về diện tích hình phẳng, thể tích khối tròn xoay.
- Tìm được nguyên hàm của một số hàm số đơn giản dựa vào định nghĩa, bảng nguyên hàm và cách tính nguyên hàm từng phần.
- Sử dụng được phương pháp đổi biến số, phương pháp từng phần.
- Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân.
- Vận dụng linh hoạt các tính chất, công thức tính các nguyên hàm, tích phân đặc biệt.
- Tính được diện tích hình phẳng, thể tích khối tròn xoay phức tạp.
Số câu
Số điểm Tỉ lệ %
2
0,4 điểm
4%
2
0,4 điểm
4%
2
0,4 điểm
4%
1
0,2 điểm
2%
7
1,4 điểm
14%
4. Số phức
- Hiểu được cơ bản về số phức, các khái niệm liên quan đến số phức. 
- Nhận biết được dạng số phức.
- Biết cách biểu diễn hình học của số phức, môđun của số phức, số phức liên hợp.
- Thực hiện được các phép toán cộng, trừ, nhân số phức.
- Thực hiện được phép toán chia hai số phức.
- Biết tìm nghiệm phức của phương trình bậc hai với hệ số thực.
 (nếu D < 0).
- Vận dụng làm được các bài toán bài toán biện luận về số phức: Tìm số phức có modun nhỏ nhất
- Các bài toán phức tạp về số phức: phương trình, xác định số hạng
Số câu
Số điểm Tỉ lệ %
2
0,4 điểm
4%
2
0,4 điểm
4%
1
0,2 điểm
2%
1
0,2 điểm
2%
6
1,2 điểm
12%
5. Hình học không gian tổng hợp. Nón, trụ, cầu.
- Biết khái niệm khối đa diện, đa diện đều.
- Nắm được các công thức tính các yếu tố của khối đa diện.
- Nhận dạng được các yếu tố về đa diện.
- Hiểu được các khái niệm về đa diện.
- Tính được các yếu tố cơ bản: diện tích tam giác, thể tích đa diện, chiều cao...
- Tính được thể tích khối lăng trụ và khối chóp.
- Vận dụng các kiến thức về góc, khoảng cách làm bài.
- Vận dụng tính khoảng cách giữa các yếu tố điểm, đường, mặt. 
- 
Số câu
Số điểm Tỉ lệ %
3
0,6 điểm
6%
2
0,4 điểm
4%
2
0,4 điểm
4%
1
0,2 điểm
2%
8
1,6 điểm
16%
6. Hình học giải tích trong không gian.
- Biết các khái niệm hệ toạ độ trong không gian.
- Nhận dạng được phương trình mặt cầu, ptmp, ptđt. 
- Nắm được các yếu tố về đt, mp, mc.
- Hiểu được về mp, đt, mc, tích có hướng, tích vô hướng, VTCP, VTPT của đt, mp. 
- Hiểu được tâm và bán kính của mặt cầu.
- Viết được phương trình mp, đt, mặt cầu.
- Lập được: ptmp, ptđt, ptmc.
- Tính được khoảng cách và góc giữa các yếu tố đt, mp, điểm.
Vận dụng làm được các bài tập về hình chiếu, đường vuông góc chung, các bài toán về góc, khoảng cách, cực trị...
Số câu
Số điểm Tỉ lệ %
3
0,6 điểm
6%
2
0,4 điểm
4%
2
0,4 điểm
4%
1
0,2 điểm
2%
8
1,6 điểm
16%
Tổng số câu
Tổng số điểm
Tỉ lệ %
18
3,6 điểm
(36%)
15
3,0 điểm
(30%)
11
2,2 điểm
(22%)
6
1,2 điểm
(2%)
50
BẢNG MÔ TẢ CHI TIẾT NỘI DUNG CÂU HỎI 
CHỦ ĐỀ
CÂU
MỨC ĐỘ
MÔ TẢ
1. Hàm số và các bài toán liên quan
1
Nhận biết
Chỉ ra 1 hàm số luôn đồng biến trên.
2
Nhận biết
Chỉ ra điểm cực trị của hàm số trùng phương.
3
Nhận biết
Tìm GTNN của hàm số bậc hai trên.
4
Nhận biết
Bảng biến thiên hàm số.
5
Thông hiểu
Xét tính đơn điệu của hàm số bậc 3.
6
Thông hiểu
Tìm m để hàm số đạt cực đại tại 1 điểm.
7
Thông hiểu
GTNN của hàm số trên một đoạn
8
Thông hiểu
Số giao điểm của đường thẳng và đồ thị hàm số
9
Vận dụng
Xác định giá trị của tham số để hàm số có cực trị thỏa mãn một điều kiện cho trước
10
Vận dụng
Chỉ ra số đường tiệm cận của một đồ thị hàm số có chứa căn
11
Vận dụng cao
Tìm giá trị lớn nhất của biểu thức nhiều biến số
2.
Hàm số lũy thừa. Mũ, logarit.
12
Nhận biết
Nhận biết tính chất của logarit.
13
Nhận biết
Nhận biết tính đơn điệu của hàm số mũ cơ số a: .
14
Nhận biết
Giải phương trình lôgarit dạng .
15
Nhận biết
Giải bất phương trình dạng .
16
Thông hiểu
Biểu diễn giá trị logarit theo 1 giá trị logarit khác.
17
Thông hiểu
Giải bất phương trình logarit bằng pp đặt ẩn phụ.
18
Thông hiểu
Giải phương trình mũ bằng pp đặt ẩn phụ.
19
Vận dụng thấp
Giải quyết bài toán phương trình mũ chứa tham số.
20
Vận dụng thấp
Tìm TXĐ của hàm số logarit kết hợp giải bpt chứa dấu giá trị tuyệt đối.
21
Vận dụng cao
Vận dụng tính chất lũy thừa vào bài toán thực tế.
3.
Tích phân và ứng dụng.
22
Nhận biết
Tìm nguyên hàm theo bảng nguyên hàm
23
Nhận biết
Công thức tính thể tích khối tròn xoay
24
Thông hiểu
Áp dụng tính chất của tích phân
25
Thông hiểu
Tính diện tích hình phẳng giới hạn bởi một đường cong ,
trục hoành và hai đường thẳng x = a , x = b
26
Vận dụng thấp
Tìm yếu tố trong tích phân
27
Vận dụng thấp
Tính diện tích hình phẳng giới hạn bởi hai đường cong
28
Vận dụng cao
Áp dụng tính diện tích hình phẳng tìm tỉ số diện tích
4.
Số phức
29
Nhận biết
Số phức liên hợp, môđun của số phức.
30
Nhận biết
Phần thực và phần ảo của số phức
31
Thông hiểu
Giải phương trình bậc hai với hệ số thực.
32
Thông hiểu
Các phép toán trên số phức
33
Vận dụng
Tổng hợp các phép toán của số phức
34
Vận dụng cao
Liên hệ tính chất hình học của số phức.
5.
Hình học không gian tổng hợp. Nón, trụ, cầu.
35
Nhận biết
Nhận biết về đường cao của lăng trụ đứng
36
Nhận biết
Nhận biết về hình bát diện.
37
Nhận biết
Nhận biết về góc giữa đường thẳng và mặt phẳng
38
Thông hiểu
Xác định và tính đường cao của hình chóp có cạnh bên vuông góc với đáy.
39
Thông hiểu
Hiểu về mối quan hệ giữa lăng trụ và hình trụ.
40
Vận dụng
Vận dụng tính thể tích của một khối đa diện
41
Vận dụng
Vận dụng về khoảng cách giữa 2 đường thẳng chéo nhau
42
Vận dụng cao
Vận dụng xác định và tính khoảng cách giữa hai đường thẳng chéo nhau
6.
Phương pháp tọa độ trong không gian.
43
Nhận biết
Nhận biết về độ dài của véc tơ
44
Nhận biết
Nhận biết về phương trình mặt cầu
45
Nhận biết
Nhận dạng về đường thẳng
46
Thông hiểu
Hiểu về tích vô hướng của hai véc tơ
47
Thông hiểu
Hiểu về khái niệm về hai véc tơ bằng nhau
48
Vận dụng
Vận dụng về tọa độ và tích vô hướng của hai véc tơ
49
Vận dụng
Tìm tọa độ điểm thỏa mãn ptmp và điều kiện về khoảng cách
50
Vận dụng cao
Vận dụng lập phương trình đường thẳng thỏa mãn điều kiện
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2017
Môn Toán
Thời gian: 90 phút
Câu 1.Trong các hàm số sau, hàm số nào đồng biến trên?
A..
 B..
C..
 D..
Câu 2.Số điểm cực trị của hàm số là:
A.3.
 B. 2.
C. 1.
 D. 0.
Câu 3.Giá trị nhỏ nhất của hàm sốlà:
A. 	B.	C. 	D.
Câu 4. Bảng biến thiên sau đây là của hàm số nào?
 x - 1 
y’ + +
y 2
 2 
A.
B.
C.
D.
Câu 5. Cho hàm số. Hãy tìm mệnh đề sai trong các mệnh đề sau?
 A.tăng trên khoảng. B.tăng trên khoảng.
 C.giảm trên khoảng. D.giảm trên khoảng.
Câu 6.Với giá trị nào củathì hàm sốđạt cực đại tại điểm?
A.
B.
C.
D.
Câu 7.Tìm giá trị lớn nhất và nhỏ nhất của hàm sốtrên đoạn?
A. 
B. 
C. 
D.
Câu 8. Với giá trị nào của m phương trìnhcó 3 nghiệm phân biệt?
A.
B.
 C. 
 D.
Câu 9. Với giá trị nào của m thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt có hoành độthỏa mãn
A.
B.
C.
D.
Câu 10. Cho đồ thị và đường thẳng. Khi cắt tại 2 điểm phân biệt và tiếp tuyến với tại hai điểm này song song với nhau thì phải bằng?
A.
B.
C.
 D.
Câu 11. Cho các số thực thỏa mãn . Giá trị lớn nhất của là:
A. 7	 B. 1	 C. 2 	D. 3
Câu 12. Cho hai số dương a, b, . Mệnh đề nào dưới đây sai?
A.	B. 	 C.	D. 	
Câu 13. Trong các hàm số sau, hàm số nào đồng biến trên tập xác định?
A. 	B.	 C. 	D. 
Câu 14. Tìm nghiệm của phương trình: .
A. 	B. 	 C. 	 D.
Câu 15. Tìm tập nghiệm của bất phương trình.
A.	 	B. 	C. 	D. 
Câu 16. Cho Hãy tínhtheo
A. 	B. 	C.	D. Đáp án khác.
Câu 17. Giảibấtphươngtrình.
A.	B.	C.	D. 
Câu 18. Tổng các nghiệm của phương trình: là:
A.3	B.4	C. 5	D. 6
Câu 19. Tìm tập hợp T tất cả các giá trị của tham số m để phương trìnhcó hai nghiệm phân biệt.
A.	 B.	C. 	D.
Câu 20. Tập xác định của hàm số là:
A. .	B. .	C.. D. .
Câu 21. Một khu rừng có trữ lượng gỗ mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ? (tìm đáp án chính xác nhất)
A. 480.660	B. 486.060	C. 586.060 D. 486.660
Câu 23: Tìm nguyên hàm của hàm sổ là:
A. 	B. 	C. 	D. .
Câu 24: Thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số liên tục, trục Ox và hai đường thẳng x = a, x = b (với ) quanh trục Ox được tính bởi công thức:
A. B. C. D. .
Câu 25: Cho hàm số có đạo hàm trên đoạn [-1;3], biết và.
Tính 
A. I = 3	 B. I = 7 C. I = -7 D. I = -10 .
Câu 26: Diện tích hình phẳng giới hạn bởi hàm số và trục hoành là S, khi đó: 
A. 	 B. C. D. .
Câu 27: Biết với a, b là những số nguyên. Tính 
A. 	 B. 	 C. 	 D. .
Câu 28: Tính diện tích hình phẳng giới hạn bởi các đường ,và x = 1
A. B. C. D. .
Câu 29: Prabol chia hình tròn có tâm tại gốc tọa độ, bán kính thành hai phần. Gọi S1 là diện tích phần giới hạn bởi Parabol và đường tròn, S2 là phần diện tích còn lại. Khi đó tỉ số là: 
A. B. C. D. .
Câu 30: Cho số phức z = 5 - 4i. Liên hợp của số phức z có môđun là:
A. 1 B. C. 3 D. 9
Câu 31. Cho số phức z = 2 + i. Phần thực và phần ảo của số phức lần lượt là:
Câu 3: Phương trình có nghiệm là:
Câu 32. Số phức bằng :
Câu 33. Cho số phức z thoả mãn điều kiện: .Phần ảo của số phức là:
Câu 34. Trong mặt phẳng phức, cho 3 điểm A,B,C lần lượt là 3 điểm biểu diễn cho 3 số phức
. Để tam giác ABC vuông tại B thì a bằng bao nhiêu:
Câu 35. Cho lăng trụ đứng ABC.A’B’C’ đường cao của hình lăng trụ là:
A. AB 	B. AB’ 	 	C. AC’ 	D. A’A.
Câu 36. Số đỉnh của một hình bát diện đều là:
 A. Sáu	 	B. Tám	 	C. Mười	 	D. Mười hai
Câu 37. Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và mặt phẳng đáy là:
Câu 38. Cho hình chóp S.ABCD, đáy là hình vuông cạnh a, SA vuông góc mặt đáy, góc giữa mp(SBD) và mặt đáy bằng 600. Đường cao của khối chóp là:
A. 	B. 	C. 	D. 
Câu 39. Một hình trụ ngoại tiếp hình lăng trụ tam giác đều với tất cả các cạnh bằng a có diện tích xung quanh bằng?
A. 	B. 	C. 	D. 	
Câu 40. Cho hình lập phương ABCD.A’B’C’D’ cạnh a, tâm O. Thể tích khối tứ diện AA’B’O là:
 	A. 	B. 	C. 	D. 
Câu 41. Cho lăng trụ có đáy là tam giác đều cạnh a , Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA’ và BC bằng . Khi đó thể tích của khối lăng trụ là:
 	A. 	B. 	C. 	D. 
Câu 42. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a. Tam giác SAD là tam giác đều và (SAD) nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SB là:
	 A. 	B. 	 C. 	D. 
Câu 43. Trong không gian với hệ tọa độ , cho . Tìm độ dài của vectơ 
 A. 	B. 	 C. 0	D. 1
Câu 44. Trong các phương trình sau, phương trình nào là phương trình mặt cầu:
A. 	B. 	
C. 	D. 
Câu 45. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: . Véc tơ chỉ phương của đường thẳng d là:
	A. 	B. 	C. 	D. 
Câu 46. Trong không gian với hệ tọa độ Oxyz, cho hai vec tơ và . Tìm giá trị của m để 
4	B. -2	C. -4 	D. 2
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với , , . Tìm tọa độ đỉnh D sao cho ABCD là hình bình hành. 
	A. 	B. 	C. 	D. 
Câu 48. Trong không gian với hệ tọa độ Oxyz, cho ba điểm , , . Tìm giá trị của m để tam giác MNP vuông tại M.
A. 	B. 	C. 	D. 
Câu 49. Trong không gian với hệ tọa độ Oxyz, cho ba điểm và ; . Tìm tọa độ điểm thuộc mặt phẳng và cách đều ba điểm 
A. 	B. 	C. 	D. 
Câu 50. Trong không gian với hệ tọa độ Oxyz, cho các đường thẳng ; ; . Đường thẳng d cắt các đường thẳng d1, d2 và song song với đường thẳng d3 có phương trình là: 
A. 	B. 	
C. 	D.