Đề thi thử THPT quốc gia năm 2015 môn: Toán (kèm đáp án)

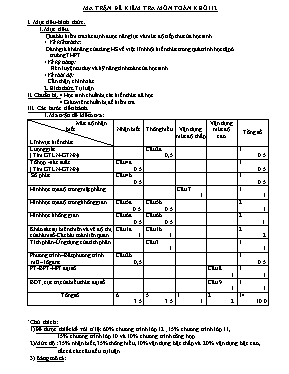
MA TRẬN ĐỀ KIỂM TRA MÔN TOÁN KHỐI 12
I. Mục tiêu-hình thức.
 1.Mục tiêu. 
 Qua bài kiểm tra xác định được năng lực và mức độ tiếp thu của học sinh. 
+ Về kiến thức: 
 Đánh giá khả năng của từng HS về việc lĩnh hội kiến thức trong quá trình học tập ở 
 trường THPT.
 +Về kỹ năng: 
 Rèn luyện tư duy và kỹ năng tính toán của học sinh.
 +Về thái độ:
 Cẩn thận, chính xác.
2.Hình thức. Tự luận
II. Chuẩn bị. · Học sinh chuẩn bị các kiến thức đã học.
 · Giáo viên chuẩn bị đề kiểm tra.
III. Các bước tiến hành.
1.Ma trận đề kiểm tra:
 Mức độ nhận biết
Lĩnh vực kiến thức
Nhận biết
Thông hiểu
Vận dụng mức độ thấp 
Vận dụng mức độ cao
Tổng số
Lượng giác
( Tìm GTLN-GTNN)
Câu 2a
0,5
1
0.5
Tổ hợp –xác suất
( Tìm GTLN-GTNN)
Câu 4a
0.5
1
0.5
 Số phức
Câu 4b
0.5
1
0.5
Hình học tọa độ trong mặt phẳng
Câu 7
1
1
1
Hình học tọa độ trong không gian
Câu 5a
 0.5 
Câu5b
0.5
2
1
Hình học không gian
Câu 6a
0.5
Câu 6b 
0.5
2
 1
Khảo sát sự biên thiên và vẽ độ thị của hàm số-Các bài toán liên quan.
Câu 1a 
 1
Câu 1b
1
2
 2
Tích phân -Ứng dụng của tích phân
Câu 3
1
1
1
Phương trình –Bất phương trình 
 mũ – lôgarit 
Câu 2b
0,5
1
0.5
PT-BPT-HPT đại số
Câu 8
1
1
1
BĐT; cực trị của biểu thức đại số
Câu 9
1
1
1
Tổng số 
6
3.5
5
3.5
1
1
2
2
14
10.0
*Chú thích: 
 1)Đề được thiết kế với tỉ lệ: 60% chương trình lớp 12 ;15% chương trình lớp 11, 
 15% chương trình lớp 10 và 10% chương trình tổng hợp.
 2)Mức độ: 35% nhận biết,35% thông hiểu,10% vận dụng bậc thấp và 20% vận dụng bậc cao,
 tất cả các câu đều tự luận.
 3) Bảng mô tả:
 Câu 1: (2,0 điểm)
 a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
 b) Viết pt tiếp tuyến,tìm m thỏa điều kiện cho trước, tìm trên đồ thị những điểm có tính chất cho 
 trước
 Câu 2: (1,0 điểm)
 a)Giải phương trình lượng giác.
 b)Giải pt-bpt mũ và logarit.
 c) Tìm GTLN-GTNN của hàm số.
 Câu 3: (1,0 điểm):
 a) Tính xác suất. 
 b) Số phức.
 Câu 4: (1,0 điểm):
 Tính tích phân-ứng dụng tích phân. 
 Câu 5: (1,0 điểm):
 Phương pháp tọa độ trong không gian:
 -Xác định tọa độ giao điểm của đường thẳng và mặt phẳng.
 - Viết phương trình mặt phẳng,đường thẳng,mặt cầu thỏa điều kiện cho trước.
 Câu 6: (1,0 điểm):
 Hình học không gian:
 -Tính thể tích
 -Tính khoảng cách.
 Câu 7: (1,0 điểm):
 Phương pháp tọa độ trong mặt phẳng:
 Tìm tọa độ điểm,viết phương trình đường thẳng,đường tròn,elip.
 Câu 8: (1,0 điểm):
 Phương trình, bất phương trình,hệ phương trình đại số.
 Câu 9: (1,0 điểm):
 Bất đẳng thức; cực trị của biểu thức đại số.
..
SỞ GIÁO DỤC VÀ ĐÀO TẠO QUẢNG NAM
CỤM CHUYÊN MÔN 11
ĐỀ CHÍNH THỨC
 KỲ THI THỬ THPT QUỐC GIA NĂM 2015 
Môn: TOÁN
Thời gian làm bài: 180 phút; 
Không kể thời gian giao đề 
Họ và tên thí sinh:lớp:
SBD:.Phòng thi
Câu 1: (2,0 điểm) Cho hàm số y = x+ 2mx+(m+3)x + 4 (C) 
 a) Khảo sát sự biến thiên và xẽ đồ thị (C) của hàm số khi m = 0.
 b) Cho điểm I(1;3). Tìm m để đường thẳng d: y = x + 4 cắt (C) tại 3 điểm phân biệt A(0;4), 
 B,C sao cho tam giác IBC có diện tích bằng 4.
Câu 2:( 1,0 điểm) Giải các phương trình sau: 
a) 4Sinx + Cosx = 2 + Sin2x
b) 
Câu 3: (1,0 điểm) Tính tích phân: I = 
Câu 4: (1,0 điểm) 
 a) Một tổ 11 người gồm 5 nam và 6 nữ,chọn ngẫu nhiên 5 người tham gia lao động.
 Tính xác suất để 5 người được chọn ra có đúng 3 nữ.
 b) Tính mô đun của số phức sau: z = (2-i)- (1+2i).
 Câu 5: (1,0 điểm) 
 Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x + y – 2z -1= 0 
 a)Tìm tọa độ giao điểm A của trục Oy và mặt phẳng (P).
 b)Viết phương trình mặt phẳng (Q) chứa đường thẳng trục Oy và vuông góc với mặt phẳng (P).
Câu 6: ( 1,0 điểm) 
 Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,SC = , hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm H của AB. 
 a)Tính theo a thể tích khối chóp S.ABCD
 b) khoảng cách từ B đến mặt phẳng (SAC).
Câu 7(1,0 điểm) 
 Trong mặt phẳng tọa độ Oxy,cho hình chữ nhật ABCD có phương trình đường thẳng : 
 AB: x – 2y + 1 = 0, phương trình đường thẳng BD: x -7y +14 =0.Viết phương trình tổng quát của đường thẳng AC,biết đường thẳng AC đi qua điểm M(2;1).
Câu 8: (1,0 điểm) Giải hệ phương trình: 
Câu 9:( 1,0 điểm) Cho x,y,z là 3 số thực dương .Tìm giá trị nhỏ nhất của biểu thức : 
 P =.
 HẾT
Giám thị coi thi không giải thích gì thêm.
ĐÁP ÁN
Câu
Nội dung
Điểm
Câu 1
(2,0điểm)
a)Khi m= 0 ta có : y = x+ 3x + 4
 *Tập xác định : D = R
*Sự biến thiên : 
- Chiều biến thiên : y’= 3x+ 3  ; y’> 0 ,
 -Hàm số đồng biến trên R và hàm số không có cực trị.
 - Giới hạn :  ;= +
..
- Bảng biến thiên :
 x - +
 y’ +
 +
 y 
 -
.
 -Đồ thị : y
 8
 4
 -1 1 x
 0
0,25
0,25
.
0,25
.
0,25
b)Phương trình hoành độ giao điểm của (C) và d :x+ 2mx+(m+3)x + 4 =x + 4(1)
 x(x +2mx + m + 2) = 0 
(1) có 3 nghiệm phân biệt (2) có 2 nghiệm phân biệt khác 0
 (*)
 Khi đó x,xlà các nghiệm của (2) x+ x= - 2m , x.x= m + 2 
S = 4d(I;d).BC = 4= 4(x+ x)- 4x.x-16= 0
 . 
 m- m – 6 = 0 .Kết hợp ĐK (*) m = 3.
 Vậy với m = 3 thỏa yêu cầu của bài toán.
0,25
0,25
.
0,25
..
0,25
Câu 2
(1điểm)
4Sinx + Cosx = 2 + Sin2x (1) 
 4Sinx + Cosx = 2 + 2 Sinx.Cosx 2Sinx(2 –Cosx) – (2 – Cosx) = 0
 (2 – Cosx) ( 2Sinx -1) = 0
.............................................................................................................................. 
Vậy họ nghiệm của (1) là: 
.......................................................................................................................................
 b) (1)
 ĐKXĐ: x > 3 (*)
 Với ĐK (*) (1) 
 = 2 
.............................................................................................................................
 Vậy nghiệm của (1) x = 5
0,25
........
0,25
........
0,25
.........
0,25
Câu 3
(1 điểm)
Câu 4
(1 điểm)
 I = . Đặt t = t= 3 + lnx 
 2tdt = tdt = 
 Đổi cận: x = 1 t = , x = e t = 2
 I = = = 
a)Không gian mẫu: = = 462
Gọi A là biến cố 5 người được chọn ra có đúng 3 nữ, suy ra = = 200.
 Vậy xác suất P(A) = = 
...............................................................................................................................
z = (2-i)-(1+2i) = 4 – 4i + i-1 -2i = 2 -6i 
Suy ra = = 2
0,25
0,25
0,25
0,25
.
0,25
0,25
..
0,25
0,25
Câu 5
(1 điểm)
a)Gọi A(0,y,0) là giao điểm của Oy và (P),
 khi đó thay x = 0 và z = 0 vào pt mp (P) ta được : y = 1.Suy ra A(0 ;1 ;0)
 b) VTCP của Oy : = (0 ;1 ;0)
 VTPT của mặt phẳng (P) := (2 ;1 ;-2) .
Mặt phẳng (Q)chứa trục Oy và (P) suy ra VTPT của (Q) : = = (-2 ;0 ;-2) 
 .. 
 PT mp (Q) : x + z + C = 0
 Oy(Q) O(Q) = 0 Vậy pt mp (Q) : x + z = 0.
 0,25
0,25
0,25
.
0,25
Câu 6
(1 điểm)
 a) Tam giác BHC vuông tại B,suy ra HC = = 
 Tam giác SHC vuông tại H,suy ra SH = = 2a
 ...................................................... .....................................................................
 V = SH. S= 
Vẽ hình sai không chấm bài giải: S
 K
 A H B 
 N 
 O
 D C
0,25
.
0,25
b)Gọi O là giao điểm ACBD
 Qua H dựng đt // BD, cắt AC tại N Suy ra HN =OB = 
 và AC(SHN)
Trong SHN dựng HK,suy ra HK(SAC) 
 .................................................................................................................................. 
 d(B,(SAC)) = 2HK=2.= 
0,25
........
0,25
Câu 7
(1 điểm)
VTCP của đường thẳng AB := (2 ;1) 
VTCP của đường thẳng BD : = (7 ;1)
Gọi VTCP của đường thẳng AC là = (a ;b), với a+ b0.
 A D
 I
 B C
 ..................................................................................................................................... 
Gọi I là giao điểm của AC và BD,suy ra tam giác ABI cân tại I 
 Suy ra Cos(BAI) = Cos(ABI) = = 
 2(2a + b)= 9(a+ b) 
 a- 8ab + 7b= 0 
+ a = b ,suy ra một VTCP của đường thẳng AC: = (1;1) 
 PTCT của đt AC: PTTQ của AC: x –y -1 = 0
..................................................................................................................................
+ a = 7b, suy ra một VTCP của đường thẳng AC: = ( 7;1),suy ra không tồn tại phương trình đường thẳng AC vì cùng phương với .
 Vậy PTTQ của AC: x – y -1 = 0 .
0,25
.........
0,25
0,25
.........
0,25
Câu 8
(1 điểm)
 ĐKXĐ : x, (1) 4+ = 4y+ y (3) 
 .. 
Xét hàm số g(t) = t+ t, g’(t) = 3t+1> 0 ,
 Suy ra hàm số g(t) = t+ t đồng biến trên R . 
 Suy ra (3) có nghiệm khi y = . Thay y = vào (2) ta được : 
 4x- 8x + 2()+ (2x -1) - 2+3 = 0
 (2x-1) + 2()-(2x-1) - 2= 0 
 ( thỏa mãn)
 Vậy nghiệm của hệ đã cho là : ) và (1 ;1) 
0,25
..
0,25
.
0,25
.
0,25
Câu 9
(1 điểm)
 Áp dụng BĐT Cau-Chy : 2 y + 2z 
 . 
 Áp dụng BĐT Bunhiacôpxki : (1+1) 
 (x+z) + y 
 Suy ra P= - 
 .
 Đăt t = x + y + z, t > 0. Xét hàm số f(t) = - , với t > 0.
 f ’(t) = - + = = 
 f ’(t) = 0 15t-6t -9 = 0 
 Bảng biến thiên :
 x 0 1 +
 f ’(x) - 0 +
 f(x) 
 .
Từ BBT suy ra f(t) f(1) = -với mọi t >0 
P= - khi 
0,25
.
0,25
..
0,25
.
0,25
*Hoc sinh giải cách khác đúng vẫn cho điểm tối đa.