Đề thi thử THPT Quốc gia môn Toán - Mã đề thi 123 - Năm học 2016-2017 - Trường THPT Hàm Rồng

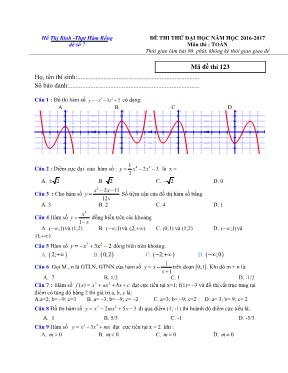
Hồ Thị Bình -Thpt Hàm Rồng 
đề số 7 
ĐỀ THI THỬ ĐẠI HỌC NĂM HỌC 2016-2017 
Môn thi : TOÁN 
Thời gian làm bài 90 phút, không kể thời gian giao đề 
 Mã đề thi 123 
Họ, tên thí sinh:.......................................................................... 
Số báo danh:............................................................................... 
Câu 1 : Đồ thị hàm số 3 23 2y x x    có dạng: 
A B C D 
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Câu 2 : Điểm cực đại của hàm số : 4 2
1
2 3
2
y x x   là x = 
A. 2 B. 2 C. 2 D. 0 
Câu 3 : Cho hàm số 
2 2 11
12
x x
y
x
 
 .Số tiệm cận của đồ thị hàm số bằng 
A. 3 B. 2 C. 4 D. 1 
Câu 4 Hàm số 
2
1
x
y
x


 đồng biến trên các khoảng 
A. ( ;1) và (1;2) B. ( ;1) và (2; ) C. (0;1) và (1;2) D. ( ;1) và 
(1; ) 
Câu 5 Hàm số 3 23 2y x x    đồng biến trên khoảng: 
A.  2; B.  0;2 C.  2;  D.  ;0 
Câu 6 Gọi M , n là GTLN, GTNN của hàm số 
1
1


x
xy trên đoạn [0;1]. Khi đó m + n là: 
A. 7 B. 1/2 C. 1 D. -1/2 
Câu 7 : Hàm số cbxaxxxf  23)( đạt cực tiểu tại x=1; f(1)= –3 và đồ thị cắt trục tung tại 
điểm có tung độ bằng 2 thì giá trị a, b, c là: 
A.a=2; b= –9; c=3 B. a= –3; b= –9; c= –2 C. a=3; b= –9; c=2 D. a= 3; b= 9; c= 2 
Câu 8 Đồ thị hàm số 352 23  xmxxy đi qua điểm (1; -1) thì hoành độ điểm cực tiểu là: 
A. 1 B. 5/3 C. -1 D. -5/3 
Câu 9 Hàm số 3 23y x x mx   đạt cực tiểu tại x = 2 khi : 
A. 0m  B. 0m  C. 0m  D. 0m  
Câu 10 Đường thẳng đi qua 2 điểm cực trị của hàm số xxy  3 có phương trình là: 
A. xy
3
2
 B. y = 1 C. xy
3
2
 D. y=x 
Câu 11 Tìm câu sai trong các mệnh đề sau về GTLN và GTNN của hàm số 
 3 3 1 , 0;3y x x x    
A. Min y = 1 B. Max y = 19 
C. Hàm số có GTLN và GTNN D. Hàm số đạt GTLN khi x = 3 
Câu 12 Phương trình 
2 75 125x  có nghiệm x bằng: 
A. 2 B. -2 C. 5 D. -5 
Câu 13 Lôgarit cơ số 
4a của 8a ( 0 1a  ) bằng: 
A. 
1
2
 B. 
1
2
 C. 2 D. -2 
Câu 14 Hàm số  ( ) ln cosh x x có đạo hàm tại điểm 
4
x

 là: 
A. '( ) 2
4
h

 B. '( ) 1
4
h

 C. '( ) 2
4
h

  D. '( ) 1
4
h

  
Câu 15 : Tìm mệnh đề sai? 
A. Hàm số 4
3
logy x luôn đồng biến. 
B. Lôgarit cơ số 0,2 của 3 luôn có giá trị âm. 
C. Lôgarit cơ số 2 của 3 luôn có giá trị dương. 
 D. Hàm số 
2
logy x luôn nghịch biến 
Câu 16 Rút gọn : 
 
4
3 24
3 12 6
.
.
a b
a b
 ta được : 
A.a
2
 b ; B.ab
2
 ; C.a
2
 b
2
; D.ab 
Câu 17 Giải phương trình 3x + 6x = 2x. Ta có tập nghiệm bằng : 
 A). 1. B). 2. C). . D). - 1. 
Câu 18 Giải phương trình    3
3
log 9 log 3 1xx x x  . Ta có nghiệm. 
A). x = 0 v x = - 3. B). x = 1 v x = 
1
27
. C). x = 1 v x = 27. D). x = 0 v x = 3 3 . 
Câu 19 BÊt ph¬ng tr×nh: 
x x 14 2 3  cã tËp nghiÖm lµ: 
A.  1; 3 B.  2; 4 C.  2log 3; 5 D. 
 2; log 3 
Câu 20 Tìm m để phương trình 1 3 1 3 4 14.2 8x x x x m        có nghiệm. 
A). - 41  m  32. B). - 41  m  - 32. C). m  - 41. D). m . 
Câu 21 Hµm sè y =  2ln x x 2 x   cã tËp x¸c ®Þnh lµ: 
 A. (-; -2) B. (1; +) C. (-; -2)  (2; 
+) D. (-2; 2) 
Câu 22 Với F(x) là nguyên hàm của hàm số  
2
2 1
f x
x x
   biết rằng F(1) = 1, F(x) là biểu 
thức nào sau đây? 
 A;  
1
2ln 2F x x
x
    ; B;  
1
2 2F x x
x
    
 C;  
1
2lnF x x
x
   D;  
1
2 4F x x
x
    
Câu 23 Xác định một nguyên hàm 
4 3
2
3 2 5
.
x x
I dx
x
 
  thoả mãn F(1) = 2 
 A; 3 2
5
( ) 5F x x x
x
    B; 3 2
5
( ) 3F x x x
x
    
 C; 3 2
5
( ) 5F x x x
x
    D; 3 2
5
( ) 7F x x x
x
    
Câu 24 . Dân số nước ta hiện nay khoảng 89.709.000 người, tỉ lệ tăng dân số hàng năm là 1,1% 
. Hỏi với mức tăng dân số hàng năm không thay đổi thì sau bao nhiêu năm nữa dân số nước ta là 
100 triệu người? 
A. 10; B. 12; C. 8; D. 14 
Câu 25 Cho tích phân 
2
2
sin 3
0
.sin cosxI e x xdx

  . Nếu đổi biến số 
2sint x thì 
A.
1 1
0 0
2 t tI e dt te dt
 
  
 
 
B.
1 1
0 0
1
2
t tI e dt te dt
 
  
 
  C.
1
0
1
(1 )
2
tI e t dt 
 D. 
1
0
2 (1 )tI e t dt  
Câu 26 Giả sử 
4
0
2
I sin 3x sin 2xdx a b
2

   , khi đó, giá trị của a b là: 
A.
1
6
 B. 
3
10
 C. 
3
10
 D. 
1
5
Câu 27 Tính dieän tích hình phaúng giôùi haïn bôûi ñoà thò cuûa haøm soá y = sinx treân ñoaïn 
[0;2 ] vaø Ox. 
A. 1; B.2 C.3; D. 4 
Câu 28 Tính theå tích cuûa vaät theå troøn xoay, sinh ra bôûi moãi hình phaúng giôùi haïn bôûi 
caùc ñöôøng sau khi noù quay xung quanh truïc Ox: x = –1; x = 2; y = 0; y = x2–2x. 
A. 
18
5

; B. 
18
7
; C. 


18
1
5
. D. 


18
1
7
Câu 29 : Tìm mệnh đề sai trong các mệnh đề sau: 
A. Số phức z = a + bi được biểu diễn bằng điểm M(a; b) trong mặt phẳng phức Oxy 
B. Số phức z = a + bi có môđun là 2 2a b 
C. Số phức z = a + bi = 0  
a 0
b 0



D. Số phức z = a + bi có số phức đối z’ = a - bi 
Câu 30 : Cho số phức z = a + bi  0. Số phức z-1 có phần thực là: 
 A. a + b B. a - b C. 
2 2
a
a b
 D. 
2 2
b
a b


Câu 31 Cho số phức z = a + a2i với a  R. Khi đó điểm biểu diễn của số phức liên hợp của z 
nằm trên: 
 A. Đường thẳng y = 2x B. Đường thẳng y = -x + 1 
 C. Parabol y = x
2
 D. Parabol y = -x
2 
Câu 32: Phương trình bậc hai với các nghiệm: 1
1 5i 5
z
3
 
 , 2
1 5i 5
z
3
 
 là: 
A. z
2
 - 2z + 9 = 0 B. 3z
2
 + 2z + 42 = 0 C. 2z
2
 + 3z + 4 = 0 D. z
2
 + 2z + 27 = 0 
Câu 33: Trong mặt phẳng phức, gọi A, B, C lần lượt là các điểm biểu diễn của các số phức z1 = -
1 + 3i, z2 = 1 + 5i, z3 = 4 + i. Số phức với các điểm biểu diễn D sao cho tứ giác ABCD là một 
hình bình hành là: 
 A. 2 + 3i B. 2 - i C. 2 + 3i D. 3 + 5i 
Câu 34 : Trong C, phương trình z4 - 6z2 + 25 = 0 có nghiệm là: 
 A. ±3 ± 4i B. ±5 ± 2i C. ±8 ± 5i D. ±2 ± i 
Câu 35 Cho hình chóp đều S.ABC, cạnh đáy bằng a. Gọi M, N theo thứ tự là trung điểm SB, 
SC. Biết    AMN SBC , diện tích tam giác AMN bằng 
2. 2A a 
2 10
.
16
a
B 
2 3
.
16
a
C .D a 
Câu 36 Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy 
bằng   0 00 90  . Thể tích khối chóp S.ABCD theo a và  bằng 
32 tan
.
3
a
A

3 2 tan
.
6
a
B

3 2 tan
.
12
a
C

3 2 tan
.
3
a
D

Câu 37 : Cho hình chóp S.ABC đáy ABC là tam giác vuông cân với BA = BC = a, SA = a vuông 
góc với đáy. Gọi M, N là trung điểm AB và AC. Tính cosin góc giữa hai mặt phẳng (SAC) và 
(SBC) bằng 
1
.
2
A 
2
.
2
B 
3
.
2
C 
2
.
3
D 
Câu 38 Cho hinh lâp phương ABCD.A’B’C’D’ cạnh a tâm 0. Khi đó thể tích khối tứ diện 
AA’B’0 là. 
3
.
8
a
A 
3
.
12
a
B 
3
.
9
a
C 
3 2
.
3
a
D 
x 
-2 2 
x 
y 
O 
(Hình 3) 
-3i 
3i 
y 
x 
O 
(Hình 2) 
y 
2 O 
x 
-2 
(Hình 1) 
Câu 39 Cho khối trụ tròn xoay có bán kính mặt đáy bằng 2 (cm), chiều cao bằng 3 (cm). Thể 
tích của khối trụ tròn xoay này bằng: 
A. 4 (cm 3 ) B. 12 (cm 3 ) C. 48 (cm 3 ) D. 24 (cm
3
) 
Câu 40 . Cho tứ diện ABCD có cạnh AD vuông góp với mp (ABC) và cạnh BD vuông góp với 
cạnh BC. Khi quay các cạnh tứ diện đó xung quanh trục là cạnh AB, có bao nhiêu hình nón được 
tạo thành? 
 A, 1; B, 2 C, 3 D, 4 
Câu 41 Số mặt cầu chứa một đường tròn cho truớc là: 
 A, 0 B, 1; C, 2 D, vô số 
Câu 42 . Người ta xếp 7 viên bi có cùng bán kính r vào một cái lọ hình trụ sao cho tất cả các 
viên bi đều tiếp xúc với đáy, viên bi nằm chính giữa tiếp xúc với 6 viên bi xung quanh và mỗi 
viên bi xung quanh đều tiếp xúc với các đường sinh của lọ hình trụ. Khi đó diện tích đáy của cái 
lọ hình trụ là: 
 A, 216 r B, 218 r C, 29 r D, 236 r 
Câu 43 Với A(2;0;-1), B(1;-2;3), C(0;1;2).Phương trình mặt phẳng qua A,B,C là 
A.x+2y+z+1=0 B.-2x+y+z-3=0 C.2x+y+z-3=0 D.x+y+z-2=0 
Câu 44 Tìm tọa độ giao điểm M của đường thẳng d
3 2 1
3 1 5
x y z  
 
 
 và mặt phẳng (P)
2 1 0x y z    . 
A.M(1;2;3) B.M(1;-2;3) C.M(-1;2;3) D.A,B,C đều sai 
Câu 45 Trong không gian Oxyz cho mặt phẳng   : 2 2 1 0P x y z    và hai điểm 
   1; 2;3 , 3;2; 1A B  . Phương trình mặt phẳng (Q) qua A, B và vuông góc với (P) là 
A. (Q): 2x + 2y + 3z – 7 = 0 B. (Q): 2x– 2y + 3z – 7 = 0 
C. (Q): 2x + 2y + 3z – 9 = 0 D. (Q): x + 2y + 3z – 7 = 0 
Câu 46 Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( ) : 2 2 1 0P x y z    và đường 
thẳng d: 
1 3
2
1
x t
y t
z t
 

 
  
. Tọa độ điểm M trên đường thẳng d sao cho khoảng cách từ M đến mặt 
phẳng (P) bằng 3 là 
A.M1(4, 1, 2) ; M2( – 2, 3, 0) B.M1(4, 1, 2) ; M2( – 2, -3, 0) 
C.M1(4, -1, 2) ; M2( – 2, 3, 0) D.M1(4, -1, 2) ; M2( 2, 3, 0) 
Câu 47 Trong không gian với hệ tọa độ Oxyz, cho hai điểm    4;2;2 , 0;0;7A B và đường 
thẳng 
3 6 1
:
2 2 1
x y z
d
  
 

.Điểm C thuộc đường thẳng d sao cho tam giác ABC cân đỉnh A 
là 
A. C(-1; 8; 2) hoặc C(9; 0; -2) B. C(1;- 8; 2) hoặc C(9; 0; -2) 
C. C(1; 8; 2) hoặc C(9; 0; -2) D. C(1; 8; -2) hoặc C(9; 0; -2) 
Câu 48 Trong khoâng gian Oxyz, viết phương trình mặt phẳng(P) chứa đường thẳng (d) : 
x y 2 0
2x z 6 0
  

  
 sao cho giao tuyến của mặt phẳng (P) và mặt cầu (S) : 
2 2 2x y z 2x 2y 2z 1 0       là đuờng tròn có bán kính r = 1. 
A
1
2
(P) : x y z 4 0
(P ) : 7x 17y 5z 4 0
   

   
; B. 
    

   
1
2
(P ) : 2x 3y z 4 0
(P ) : 7x 17y 5z 4 0
; 
C. 
    

   
1
2
(P ) : x y z 4 0
(P ) : x 7y 5z 4 0
; D.
    

   
1
2
(P ) :2x 3y z 4 0
(P ) : x 7y 5z 4 0
Câu 49 Trong khoâng gian Oxyz cho A(0; 1; 0), B(2; 2; 2), C(-2; 3; 1) vaø ñöôøng thaúng 
() : 
x 1 y 2 z 3
2 1 2
  
 

Tìm ñieåm N thuoäc () ñeå theå tích tam giaùc ABN nhoû 
nhaát.
A(-3; 0; 1). B. (3;0;1). C. (-3; 0; -1); D. (0;-3;1) 
Câu 50 Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng   : 2 2 1 0x y z     và mặt cầu 
       
2 2 2
: 1 2 1 9S x y z      . Viết phương trình mặt phẳng   song song với 
  và tiếp xúc với mặt cầu  S , tìm tọa độ tiếp điểm tương ứng. 
A.      : 2x y 2z 7 0 B.      1 : 2x y 2z 7 0 ,      2 : 2x y 2z 11 0 
C.      : 2x y 2z 11 0 ; D.      1 : 2x y 2z 7 0      2 : 2x y 2z 11 0 ; 
D A 
 24A 30C 
31C 32B 33B 34D 
 43C 44D 45A 46A 47C 48A 49A 50B