Đề thi thử THPT quốc gia môn Toán 2017 - Trường THPT Ý Yên

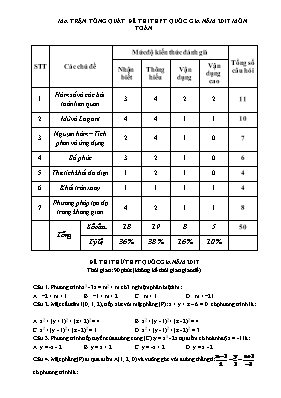
MA TRẬN TỔNG QUÁT ĐỀ THI THPT QUỐC GIA NĂM 2017 MÔN TOÁN
STT
Các chủ đề
Mức độ kiến thức đánh giá
Tổng số câu hỏi
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
1
Hàm số và các bài toán liên quan
3
4
2
2
11
2
Mũ và Lôgarit
4
4
1
1
10
3
Nguyên hàm – Tích phân và ứng dụng
2
4
1
0
7
4
Số phức
3
2
1
0
6
5
Thể tích khối đa diện
1
2
1
0
4
6
Khối tròn xoay
1
1
1
1
4
7
Phương pháp tọa độ trong không gian
4
2
1
1
8
Tổng
Số câu
18
19
8
5
50
Tỷ lệ
36 %
38 %
16 %
10 %
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2017
Thời gian: 90 phút (không kể thời gian giao đề)
Câu 1. Phương trình x3 - 3x = m2 + m có 3 nghiệm phân biệt khi:
A. −2 −21
Câu 2. Mặt cầu tâm I(0; 1; 2), tiếp xúc với mặt phẳng (P): x + y + z – 6 = 0 có phương trình là:	 
A. x2 + (y + 1)2 + (z + 2)2 = 4	B. x2 + (y - 1)2 + (z - 2)2 = 4
C. x2 + (y - 1)2 + (z - 2)2 = 1	D. x2 + (y - 1)2 + (z - 2)2 = 3
Câu 3. Phương trình tiếp tuyến của đường cong (C): y = x3 - 2x tại điểm có hoành độ x = -1 là:
A. y = -x - 2	B. y = x + 2	C. y = -x + 2	D. y = x - 2
Câu 4. Mặt phẳng (P) đi qua điểm A(1; 2; 0) và vuông góc với đường thẳng d: có phương trình là: 
A. 2x + y – z + 4 = 0	B. –2x –y + z + 4 = 0	
C. –2x – y + z – 4 = 0	D. x + 2y – 5 = 0
Câu 5. Cho hình hộp ABCD.A’B’C’D’. Gọi M, N, K lần lượt là trung điểm của các cạnh AA’, BC và CD. Thiết diện tạo bởi mặt phẳng (MNK) với hình hộp là:
A. Lục giác	B. Tam giác	C. Tứ giác	D. Ngũ giác
Câu 6.	Hàm số y = x3 - 6x2 + mx +1 đồng biến trên miền (0; +¥) khi giá trị của m là:
A. m ≧ 12	B. m ≧ 0	C. m ≦ 12 	D. m ≦ 0
Câu 7. Đường tròn tâm I (3;−1), cắt đường thẳng d: 2x + y + 5 = 0 theo dây cung AB = 8 có phương trình là:
A. (x - 3)2 + (y + 1)2 = 4	B. (x - 3)2 + (y + 1)2 = 20
C. (x + 3)2 + (y -1 )2 = 4	D. (x - 3)2 + (y + 1)2 = 36
Câu 8. Tập hợp các số phức z thoả mãn đẳng thức |z + 2 + i| = | - 3i| có phương trình là: 
A. y = x + 1	B. y = - x + 1	C. y = -x – 1	D. y = x - 1
Câu 9. Hình chiếu vuông góc của điểm A(0; 1; 2) trên mặt phẳng (P): x + y + z = 0 có tọa độ là:
A. (–2; 2; 0) 	B. (–2; 0; 2)	C. (–1; 1; 0) 	D. (–1; 0; 1) 
Câu 10. Thể tích khối tròn xoay khi quanh hình phẳng giới hạn bởi các đường y = x2 – x + 2 và y = 2x quanh trục Ox là:
A. p 	B. p
C. p	D. p
Câu 11. Cho ΔABC có A(1; 2), B(3; 0), C(-1; -2) có trọng tâm G. Khoảng cách từ G đến đường thẳng AB bằng:
A. 2	B. 2	C. 4	D. 
Câu 12. Phương trình có nghiệm là:
A. x = 	B. x = 	C. x = 	D. x = 
Câu 13. Bất phương trình có nghiệm là:
A. < x < 2	B. 	C. 	D. 
Câu 14. Hàm số y = (m - 1)x4 + (m2 - 2m)x2 + m2 có ba điểm cực trị khi giá trị của m là: 
A. 	B. 	C. 	D. 
Câu 15. Mặt phẳng (P) chứa đường thẳng d: và vuông góc với mặt phẳng có phương trình là: 
A. x + 2y – 1 = 0	B. x − 2y + z = 0	C. x − 2y – 1 = 0 	D. x + 2y + z = 0 
Câu 16. Tích phân I = có giá trị bằng:
A. 8 ln2 - 	B. 24 ln2 – 7	C. ln2 - 	D. ln2 - 
Câu 17. Nguyên hàm của hàm số y = x.e2x là: 
A. 	B. 
C. 	D. 
Câu 18. Cấp số cộng {un} thỏa mãn điều kiện . Số hạng có giá trị là
A. 19	B. 28	C. 10	D. 91
Câu 19. Phương trình có nghiệm là: 
A. 	B. 	C. 	D. 
Câu 20. Tích phân I = có giá trị bằng:
A. 2ln3 + 3ln2	B. 2ln2 + 3ln3	C. 2ln2 + ln3	D. 2ln3 + ln4
Câu 21. Bất phương trình có nghiệm là: 
A. 	B. -2 1 
Câu 22. Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a; SA ^ (ABCD), góc giữa SC và đáy bằng 60o. Thể tích hình chóp S.ABCD bằng:
A. 	B. 	C. 	D. 
Câu 23. Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = 4a, AD = 3a; các cạnh bên đều có độ dài bằng 5a. Thể tích hình chóp S.ABCD bằng:
A. 	B. 	C. 	D. 
Câu 24. Hệ phương trình có nghiệm duy nhất khi:
A. m ¹ 0	B. m ¹ 1	C. m ¹ ±1	D. m ¹ -1
Câu 25. Cho số phức z = (2 + i)(1 − i) + 1 + 3i . Môđun của z là: 
A. 2 	B. 2 	C. 	D. 4 
Câu 26. Khoảng cách từ điểm M(1; 2; -3) đến mặt phẳng (P): x + 2y - 2z -2 = 0 bằng:
A. 1	B. 	C. 	D. 3
Câu 27. Góc giữa hai đường thẳng và bằng
A. 45o	B. 90o	C. 60o	D. 30o
Câu 28. Hàm số y = x3 – 5x2 + 3x + 1 đạt cực trị khi:
A. 	B. 	C. 	D. 
Câu 29. Phương trình sin3x + sinx = cos3x + cosx có nghiệm là:
A. 	 B. 	C. D. 
Câu 30. Phương trình các tiếp tuyến của đồ thị hàm số y = x3 - 2x2 + x đi qua điểm M(1;0) là:
A. 	B.	 	C. 	D. 
Câu 31. Lăng trụ tam giác đều ABC.A’B’C’ có góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 60o; cạnh AB = a. Thể tích khối đa diện ABCC’B’ bằng:
A. 	B. 	C. 	D. 
Câu 32. Hàm số y = x3 - 3mx2 +6mx +m có hai điểm cực trị khi giá trị của m là:
A. 	B. 0 < m < 2 	C. 0 < m < 8	D. 
Câu 33. Trong một hộp có 5 viên bi xanh và 6 viên bi đỏ. Lấy ra 4 viên bất kỳ. Xác suất để 4 viên bi được chọn có đủ hai màu là:
A. 	B. 	C. 	D. 
Câu 34. Cho hàm số y =. Giá trị y'(0) bằng:
A. -3	B. -1	C. 0	D. 3
Câu 35. Hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a; SA ^ (ABCD); góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 60o. Gọi M, N lần lượt là trung điểm của SB, SC. Thể tích của hình chóp S.ADNM bằng:
A. 	 B. 	C. 	D. 
Câu 36. Cho số phức z thỏa mãn đẳng thức z + (1 + i) = 5 + 2i . Môđun của z là:
A. 	 B. 	C. 2	D. 
Câu 37. Ba véc tơ , , thoả mãn mỗi véc tơ cùng phương với tích có hướng của hai véc tơ còn lại là:
A. (–1; 2; 7), (–3; 2; –1), (12; 6; –3).	B. (4; 2; –3), (6; – 4; 8), (2; – 4; 4)
C. (–1; 2; 1), (3; 2; –1), (–2; 1; – 4)	D. (–2; 5; 1), (4; 2; 2), (3; 2; – 4)
Câu 38. Ba véc tơ , , thoả mãn mỗi véc tơ biểu diễn được theo hai véc tơ còn lại là:
A. (–1; 3; 2), (4; 5; 7), (6; –2; 1)	B. (– 4; 4; 1), (2; 6; 2), (3; 0; 9)
C.	( 2; –1; 3), (3; 4; 6), (–4; 2; – 6)	D. (0; 2; 4), (1; 3; 6), (4; 0; 5)
Câu 39. Hai mặt phẳng (P) và (Q) có giao tuyến cắt trục Ox là:
A. (P): 4x – 2y + 5z – 1 = 0 và (Q): 2x – y + 3z – 2 = 0	
B. (P): 3x – y + z – 2 = 0 và (Q): x + y + z + 1 = 0 
C. (P): x – y – 3z + 3 = 0 và (Q): 4x – y + 2z – 3 = 0	
D. (P): 5x + 7y – 4z + 5 = 0 và (Q): x – 3y + 2z + 1 = 0
Câu 40. Mặt phẳng cắt mặt cầu (S): x2 + y2 + z2 – 2x + 2y + 6z –1 = 0 có phương trình là:
A. 2x + 3y –z – 16 = 0	B. 2x + 3y –z + 12 = 0
C. 2x + 3y –z – 18 = 0	D. 2x + 3y –z + 10 = 0
Câu 41. Cho điểm M(–3; 2; 4), gọi A, B, C lần lượt là hình chiếu của M trên Ox, Oy, Oz. Mặt phẳng song song với mp(ABC) có phương trình là:
A. 4x – 6y –3z + 12 = 0	B. 3x – 6y –4z + 12 = 0
C. 6x – 4y –3z – 12 = 0	D. 4x – 6y –3z – 12 = 0
Câu 42. Côsin của góc giữa Oy và mặt phẳng (P): 4x – 3y + z – 7 = 0 là:
A.	B. 	C. 	D. 
Câu 43. Hàm số y = 
A. Đồng biến trên khoảng (–¥; 1)	 	B. Đồng biến trên khoảng (2; +¥)
C. Nghịch biến trên khoảng (1,5; +¥)	D. Nghịch biến trên khoảng (–¥; 1,5) 
Câu 44. Hàm số y = cos2x – 2cosx + 2 có giá trị nhỏ nhất là:
A. 1 	B. 2	C. 	D. –1
Câu 45. Đồ thị hàm số y = có
A. Tiệm cận đứng là đường thẳng x = 0 khi x ® 0– 
B. Tiệm cận ngang là đường thẳng y = 1 khi x ® + ¥ và x ® – ¥
C. Tiệm cận xiên là đường thẳng y = – x – khi x ® + ¥ và khi x ® – ¥
D. Tiệm cận xiên là đường thẳng y = x – khi x ® + ¥ và khi x ® – ¥
Câu 46. Một điểm uốn của đồ thị hàm số y = sin2x có hoành độ là: 
A. 	B. 	C. 	D. 
Câu 47. Trên hệ toạ độ Oxy cho đường cong (C) có phương trình là y = x2 + 2x – 1 và hai điểm A(1; 2), B (2; 3). Tịnh tiến hệ toạ độ Oxy theo véc tơ ta được phương trình của đường cong (C) trên hệ trục toạ độ mới IXY là:
A. Y = (X + 1)2 + 2(X + 1) – 3	B. Y = (X + 2)2 + 2(X + 2) – 4
C. Y = (X + 1)2 + 2(X + 1) – 2	D. Y = (X + 2)2 + 2(X + 2) – 1
Câu 48. Hàm số y = có nguyên hàm là hàm số:
A. y = ln + C 	B. y = ln + C 
C. y = ln + C 	D. y = 2.ln + C 
Câu 49. Diện tích hình phẳng giới hạn bởi các đường y = x2 và y = 2 – x2 là:
A. 2	B. 2	C. 2	 D. 2
Câu 50. Hàm số y = 
Không có cực trị 	B. Có một điểm cực trị	
C. Có hai điểm cực trị	D. Có ba điểm cực trị
-----------Hết -----------