Đề thi thử THPT Quốc gia lần 5 môn Toán năm 2017 - Đoàn Trí Dũng

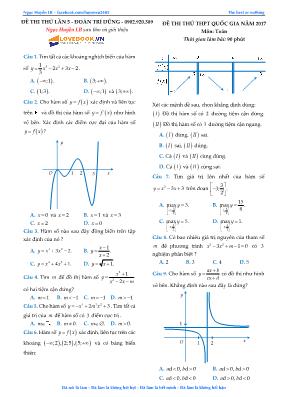
Ngọc Huyền LB – facebook.com/huyenvu2405 The best or nothing 
Đã nói là làm - Đã làm là không hời hợt - Đã làm là hết mình - Đã làm là không hối hận 
ĐỀ THI THỬ LẦN 5 - ĐOÀN TRÍ DŨNG - 0902.920.389 
Ngọc Huyền LB sưu tầm và giới thiệu 
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2017 
Môn: Toán 
Thời gian làm bài: 90 phút 
Câu 1. Tìm tất cả các khoảng nghịch biến của hàm 
số 3 2
1
2 3 2
3
y x x x    . 
 A.  ;1 . B.  3; . 
 C.  1;3 . D.  ;1 và  3; . 
Câu 2. Cho hàm số  y f x xác định và liên tục 
trên và đồ thị của hàm số  'y f x như hình 
vẽ bên. Xác định các điểm cực đại của hàm số 
 y f x ? 
 A. 0x  và 2x  B. 1x  và 3x  
 C. 2x  D. 0x  
Câu 3. Hàm số nào sau đây đồng biến trên tập 
xác định của nó ? 
 A. 3 23 2.y x x   B. 
1
.
2
x
y
x



 C. 4 24 1.y x x   D. 1.y x  
Câu 4. Tìm m để đồ thị hàm số 
2
2
1
2
x
y
x x m


 
có hai tiệm cận đứng? 
 A. 1m B. 1m  C. 1m  D. 1m  
Câu 5. Cho hàm số 4 2 22 3y x m x    . Tìm tất cả 
giá trị của m để hàm số có 3 điểm cực trị . 
 A. .m B. 0.m C. .m D. 0.m 
Câu 6. Hàm số  y f x xác định, liên tục trên các 
khoảng      ;2 , 2;5 , 5;  và có bảng biến 
thiên: 
Xét các mệnh đề sau, chọn khẳng định đúng: 
 I Đồ thị hàm số có 2 đường tiệm cận đứng. 
 II Đồ thị hàm số có 1 đường tiệm cận ngang. 
 A.  I đúng,  II sai. 
 B.  I sai,  II đúng. 
 C. Cả  I và  II cùng đúng. 
 D. Cả  I và  II cùng sai. 
Câu 7. Tìm giá trị lớn nhất của hàm số 
3 3 3y x x   trên đoạn 
3
3; .
2
 
 
 
 A. 
3
3;
2
max 3.y
 
 
 
 B. 
3
3;
2
15
max .
8
y
 
 
 
 
 C. 
3
3;
2
max 5.y
 
 
 
 D. 
3
3;
2
max 1.y
 
 
 
 
Câu 8. Có bao nhiêu giá trị nguyên của tham số 
m để phương trình 3 23 1 0x x m    có 3 
nghiệm phân biệt ? 
 A. 2 B. 3 C. 4 D. 5 
Câu 9. Cho hàm số 
x
ax b
y
c d



 có đồ thị như hình 
vẽ bên. Khẳng định nào sau đây là đúng? 
 A. d 0, d 0a b  B. d 0, d 0a b  
 C. d 0, d 0a b  D. d 0, d 0a b  
y 
O x 1 2 3 
y 
O x 
1 
2 1 
Ngọc Huyền LB – facebook.com/huyenvu2405 The best or nothing 
Đã nói là làm - Đã làm là không hời hợt - Đã làm là hết mình - Đã làm là không hối hận 
Câu 10. Cho hàm số 3 3y x ax b   có đồ thị  C . 
Gọi ,A B là hai điểm trên đồ thị  C tại đó có tiếp 
tuyến với  C song song nhau và có hệ số góc 
bằng 3. Biết rằng khoảng cách từ gốc tọa độ tới 
đường thẳng AB bằng 1? Tìm giá trị nhỏ nhất 
của 2 2P a b  ? 
 A. 
6
5
 B. 
3
2
 C. 
4
3
 D. 
7
6
Câu 11. Ông Hùng có 50m lưới hàng rào. Ông 
muốn rào miếng đất thành hai chuồng kín hình 
chữ nhật để một chuồng nuôi gà, một chuồng 
nuôi vịt. Biết hai chuồng có chung một vách ngăn 
cũng bằng lưới trên. Hỏi ông Hùng có thể rào hai 
chuồng với tổng diện tích lớn nhất bằng bao 
nhiêu ? 
 A. 2
625
.
8
m B. 2
625
.
6
m C. 2
5000
.
49
m D. 2
625
.
4
m 
Câu 12. Tính đạo hàm của hàm số  3log 2y x . 
 A. 2 ln3.y x  B. 
1
.
2 ln3
y
x
  
 C. 
1
.
ln3
y
x
  D. 4 ln3.y x  
Câu 13. Cho hàm số  5
x
y m  . Tìm tất cả giá 
trị của m để hàm số nghịch biến trên . 
 A. 4 5.m  B. 0 1.m  
 C. 4 5.m  D. 5.m 
Câu 14. Bất phương trình 
2
2 10
3 4 12
2
x
x x

     
 
 có 
bao nhiêu nghiệm nguyên dương ? 
 A. 2 B. 3 C. 4 D. 6 
Câu 15. Cho các số thực dương , ,x y z khác 1 và 
thỏa mãn 1xyz  . Tìm giá trị nhỏ nhất của biểu 
thức: 
log log log 2 log log log
z x y x y z
y xz
yx z
A z x y
y z x
 
      
 
 
 A. 4 2 B. 6 3 C. 6 2 D. 3 
Câu 16. Đường cong  C ở hình bên là đồ thị của 
1 trong 4 hàm số được liệt kê sau đây. Hỏi hàm 
số đó là hàm số nào? 
 A. .y x B. 
3
2 .y x C. 
3
1
.y
x
 D. .y x 
Câu 17. Cho , ,a b x là các số thực dương. Biết 
3 13
3
log 2log logx a b  , tính x theo a và b . 
 A. 
4
.
a
x
b
 B. .
a
x
b
 
 C. 4x a b  D. 4 .x a b  
Câu 18. Cho các số thực ,a b thỏa 
2 3
3 5a a và 
2 3
log log .
3 5b b
 Khẳng định nào sau đây là khẳng 
định đúng? 
 A. 0 log 1.
a
b  B. log 0.
b
a  
 C. log 1.
a
b  D. 0 log 1.
b
a  
Câu 19. Cho các số thực dương , ,a b c với 
1, 1.ab c  Khẳng định nào sau đây là khẳng 
định đúng ? 
 A. log log .logab a bc c c 
 B. log log log
ab a b
c c c  
 C. 
log .log
log .
log log
a b
ab
a b
c c
c
c c


 D. 
log log
log .
log .log
a b
ab
a b
c c
c
c c

 
Câu 20. Cho ,x y là các số thực dương thỏa 
9 6 4
log log log .
6
x y
x y
 
   
 
 Tính tỉ số 
x
y
. 
 A. 3.
x
y
 B. 5.
x
y
 C. 2.
x
y
 D. 4.
x
y
 
Câu 21. Xét số thực 
2 2
log log .... 2m   trong 
đó bên trong biểu thức có 2017 dấu căn thức. 
Phương trình m mx x m  có bao nhiêu nghiệm 
thực phân biệt? 
 A. 1 B. 2 
 C. 3 D. Vô nghiệm 
y 
O x 1 
1 
(C) 
Ngọc Huyền LB – facebook.com/huyenvu2405 The best or nothing 
Đã nói là làm - Đã làm là không hời hợt - Đã làm là hết mình - Đã làm là không hối hận 
Câu 22. Tìm nguyên hàm của hàm số   2 .xf x  
 A.   1.2 .xf x dx x C  B.   2 ln2 .
xf x dx C  
 C.  
12
.
1
x
f x dx C
x

 

 D.  
2
.
ln2
x
f x dx C  
Câu 23. Với mỗi số tự nhiên n , ta đặt: 
1
0
n x
n
I x e dx  . Mệnh đề nào sau đây đúng? 
 A.   12 1n nI e n I    B. 1n nI e nI   
 C. 
1n n
I e nI

  D.   11n nI e n I     
Câu 24. Cho hàm số  y f x liên tục trên và 
là hàm số chẵn. 
Biết rằng    
3 0
0 4
3, 7.f x dx f y dy

   
Tính giá trị của tích phân  
4
3
I f t dt  . 
 A. 10.I  B. 4.I  C. 
7
.
3
I  D. 21.I  
Câu 25. Tính tích phân 
1
2
0 4 3
dx
I
x x

 
 . 
 A. 
3
ln .
2
I  B. 
1 3
ln .
3 2
I  
 C. 
1 3
ln .
2 2
I   D. 
1 3
ln .
2 2
I  
Câu 26. Viết công thức tính diện tích S của hình 
phẳng D giới hạn bởi hai đồ thị hàm số  y f x , 
 y g x liên tục trên đoạn ;a b   và các đường 
thẳng , .x a x b  
 A.     .
b
a
S f x g x dx    
 B.     .
b
a
S f x g x dx  
 C.      .
b
a
S f x g x dx  
 D.     .
b
a
S f x g x dx    
Câu 27. Tính diện tích hình phẳng giới hạn bởi 
các đường 
1
x
y
x


, 3x  và các trục tọa độ? 
 A. 
8
3
 B. 3 C. 
10
3
 D. 
7
3
Câu 28. Tính thể tích khối tròn xoay giới hạn bởi 
các đường 2y x  , y x , 2x  và xoay 
quanh trục hoành. 
 A. 
10
3

 B. 
8
3

 C. 
11
3

 D. 
7
3

Câu 29. Cho số phức 1 .z i  Khẳng định nào 
sau đây là khẳng định sai ? 
 A. Phần thực z là 1 B. 2z là số thuần ảo. 
 C. .z z là số thực. D. Phần ảo của z là .i 
Câu 30. Cho số phức 
2 2
.
2 2
z i  Tìm số phức 
2016 .w z 
 A. .w i B. 1.w  C. .w i  D. 1.w   
Câu 31. Cho số phức  1z m m i   ( m là tham 
số thực). Đặt .w z iz  Tìm tất cả giá trị của m 
để w là số thuần ảo. 
 A. 
1
.
2
m  B. 1.m C. .m D. .m 
Câu 32. Cho các số phức 
1 2 1
, 1 ,z i z z  
3 1
1 .z z  Gọi , ,M N P lần lượt là các điểm biểu 
diễn các số phức 
1 2 3
, ,z z z trong mặt phẳng phức. 
Nhận xét nào sau đây đúng ? 
 A. MNP vuông. B. MNP cân. 
 C. MNP đều. D. MNP vuông cân. 
Câu 33. Gọi 
1 2
,z z là hai nghiệm của phương 
trình  2 3 2 2 2 0z i z i     trên tập số phứC. 
Tính giá trị biểu thức 2 21 2 .A z z  
 A. 5 12 .i B. 8 .i C. 1 8 .i D. 3 4 .i  
Câu 34. Cho biết 1 2iz  . Tìm giá trị lớn nhất 
của 2z  . 
 A. 2 5 B. 2 3 C. 4 D. 2 2 
Câu 35. Cho hình hộp chữ nhật .ABCD A B C D    
có , , .AB a AD b AA c   Tính thể tích V của 
khối lăng trụ .ABC A B C   . 
 A. .V abc B. 
1
.
2
V abc 
 C. 
1
.
6
V abc D. 
1
.
3
V abc 
Câu 36. Cho hình chóp .S ABC có 
5 , 7 , 8 ,AB cm BC cm AC cm   đường cao 
6SH cm . Tính thể tích V của khối chóp .S ABC ? 
 A. 340 .cm B. 335 .cm 
Ngọc Huyền LB – facebook.com/huyenvu2405 The best or nothing 
Đã nói là làm - Đã làm là không hời hợt - Đã làm là hết mình - Đã làm là không hối hận 
 C. 310 3 .cm D. 320 3 .cm 
Câu 37. Cho hình chóp tứ giác đều .S ABCD có 
thể tích .V Gọi O là tâm của đáy, , , ,M N P Q 
lần lượt là trung điểm , , , .SA SB SC SD Tính theo 
V thể tích của khối chóp .O MNPQ ? 
 A. .
4
V
 B. 
8
V
 C. .
3
V
 D. .
16
V
Câu 38. Cho hình chóp .S ABCD có đáy là hình 
vuông tâm ,O cạnh .a Cạnh bên SA h và 
vuông góc với mặt đáy. Gọi 
1
h là khoảng cách 
giữa hai đường thẳng SC và .BD Tìm mối liên 
hệ giữa 
1
, ,a h h ? 
 A. 
2 2 2
1
1 1 1
.
4h h a
  B. 
2 2 2
1
1 1 1
.
4 2h h a
  
 C. 
2 2 2
1
1 1 1
.
2h h a
  D. 
2 2 2
1
1 1 1
.
h h a
  
Câu 39. Cho tứ diện DABC có 
3, D 2AB a C a  , tất cả các cạnh còn lại đều 
bằng a . Xác định bán kính mặt cầu ngoại tiếp tứ 
diện DABC ? 
 A. 
34
8
a
R  B. 
2
2
a
R  
 C. 
17
4
a
R  D. 
3
2
a
R  
Câu 40. Bạn Duy muốn làm một vỏ hộp đựng bút 
hình trụ bằng cách cuộn một mảnh bìa cứng hình 
vuông ABCD (dán hai mép AB và ,CD phần 
giấy dán không đáng kể). Thể tích hộp bút sau 
khi hoàn thành mà bạn Duy muốn là 3
2
.dm

 Hỏi 
bạn Duy cần mảnh bìa có cạnh dài bao nhiêu? 
 A. 2 .dm B. 1 .dm C. 3 .dm D. 2,5 .dm 
Câu 41. Cho hình vuông ABCD nội tiếp đường 
tròn  C tâm O , bán kính 5 .R cm Gọi  H là 
hình gồm các điểm của hình tròn  C nhưng 
không nằm trong hình vuông .ABCD Tính thể 
tích V của khối tròn xoay sinh ra bởi hình  H 
khi quay  H quanh đường chéo AC của hình 
vuông ? 
 A. 
500
.
3
V

 B. 
125
.
2
V

 
 C. 125 .V   D. 
250
.
3
V

 
Câu 42: Một bình đựng rượu hình trụ có diện tích 
đáy (mặt trong) bằng 210 ,cm chiều cao của 
rượu trong bình là 10 .cm Người ta rót rượu ra 
những cái ly dạng phễu (như hình vẽ), có chiều 
cao 5cm (không kể phần chân đế ly), chu vi thành 
ly là 5 .cm Hỏi rượu trong bình có thể rót đầy 
bao nhiêu ly như trên? 
 A. 9 ly. B. 10 ly. 7 ly. D. 8 ly. 
Câu 43. Cho mặt phẳng  P đi qua ba điểm 
     1; 2;4 , 4; 2;0 , 3; 2;1A B C     không thẳng 
hàng. Vectơ nào sau đây là một vectơ pháp tuyến 
của mặt phẳng  P ? 
 A. .i B. .j 
 C. .k D.  1;0;1 .n  
Câu 44. Trong không gian với hệ tọa độ ,Oxyz 
cho hai điểm    3;1; 2 , 1;1;0 .A B  Viết phương 
trình mặt phẳng trung trực  P của đoạn thẳng 
AB . 
 A.   : 2 1 0.P x z   B.   : 2 0.P x y z   
 C.   : 2 3 0.P x z   D.   : 2 0.P y z   
Câu 45. cho hai mặt phẳng   : 1 0P x y z    
và   : 5 0.Q x y z    Có bao nhiêu điểm M 
trên trục Oy thỏa mãn M cách đều hai mặt 
phẳng  P và  Q ? 
 A. 0. B. 1. C. 2. D. 3. 
Câu 46. Trong không gian với hệ tọa độ ,Oxyz 
cho mặt cầu  S có tâm  1; 2;3I  và tiếp xúc với 
mặt phẳng tọa độ .Oxz Viết phương trình của 
mặt cầu  S . 
 A.      
2 2 2
1 2 3 4.x y z      
 B.      
2 2 2
1 2 3 1.x y z      
 C.      
2 2 2
1 2 3 1.x y z      
 D.      
2 2 2
1 2 3 4.x y z      
Ngọc Huyền LB – facebook.com/huyenvu2405 The best or nothing 
Đã nói là làm - Đã làm là không hời hợt - Đã làm là hết mình - Đã làm là không hối hận 
Câu 47. Trong không gian với hệ tọa độ ,Oxyz
cho điểm  3;2;1A và mặt phẳng 
  : 3 1 0.P x y z    Viết phương trình đường 
thẳng  đi qua điểm A và vuông góc với mặt 
phẳng  .P 
 A. 
3
: 2 1
3
x
y z

     
 B. 
13 1
: .
3 2 1
yx z 
   
 C. 
3 1
: 2 .
3 1
x z
y
 
   

 D. 
13
: 1.
3 2
yx
z

    
Câu 48: Tính khoảng cách giữa hai đường thẳng 
 1
1 3
: 2 ,
2 3
x z
d y
 
   
 2
3 1
: 2 .
2 3
y z
d x
 
   
 A. 
8 3
.
3
d  B. 
186
.
3
d  
 C. 
4 3
.
3
d  D. 3 3.d  
Câu 49. Cho 
12 1
:
3 2 2
yx z 
  

 và 
  : 2 2 2 0,P x y z      : 2 2 4 0.Q x y z     
Viết phương trình mặt cầu  S có tâm nằm trên 
 và tiếp xúc với hai mặt phẳng  P và  .Q 
 A. 2 2 2 4 2 2 2 0.x y z x y z       
 B. 2 2 2
170
2 6 6 0.
9
x y z x y z       
 C. 2 2 2 4 2 2 2 0.x y z x y z       
 D. 2 2 2 2 6 6 18 0.x y z x y z       
Câu 50. Giả sử điểm  ; ;M a b c nằm trên mặt 
phẳng   : 7x 5 62 0P y z    sao cho 
MA MB đạt giá trị nhỏ nhất với 
   1; 2; 5 , 1;4;7A B  . Tính P a b c   ? 
 A. 8 B. 10 C. 12 D. 14 
ĐÁP ÁN 
1.C 6.B 11.B 16.A 21.A 26.B 31.C 36.D 41.D 46.D 
2.C 7.C 12.C 17.A 22.D 27.A 32.A 37.B 42.A 47.A 
3.D 8.B 13.A 18.B 23.C 28.A 33.C 38.B 43.B 48.A 
4.D 9.A 14.B 19.C 24.B 29.D 34.A 39.B 44.C 49.D 
5.B 10.A 15.C 20.C 25.D 30.B 35.B 40.A 45.B 50.B