Đề thi thử THPT quốc gia lần 1 năm học 2016 – 2017 môn: Toán 12

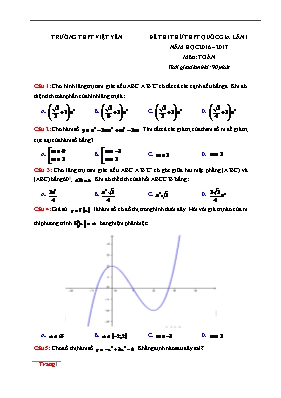
TRƯỜNG THPT VIỆT YÊN 
ĐỀ THI THỬ THPT QUỐC GIA LẦN 1
NĂM HỌC 2016 – 2017
Môn: TOÁN
Thời gian làm bài: 90 phút
Câu 1: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh đều bằng a. Khi đó diện tích toàn phần của hình lăng trụ là:
	A. 	B. 	C. 	D. 
Câu 2: Cho hàm số . Tìm tất cả các giá trị của tham số m để giá trị cực đại của hàm số bằng 3.
	A. 	B. 	C. 	D. 
Câu 3: Cho lăng trụ tam giác đều ABC.A’B’C’ có góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 600; . Khi đó thể tích của khối ABCC’B’ bằng:
	A. 	B. 	C. 	D. 
Câu 4: Giả sử là hàm số có đồ thị trong hình dưới đây. Hỏi với giá trị nào của m thì phương trình ba nghiệm phân biệt:
	A. 	B. 	C. 	D. 
Câu 5: Cho đồ thị hàm số . Khẳng định nào sau đây sai?
	A. Điểm cực đại của đồ thị hàm số là 
	B. Hàm số đồng biến trên khoảng 
	C. Đồ thị đi qua điểm 
	D. Đồ thị luôn cắt đường thẳng tại hai điểm phân biệt 
Câu 6: Trong các hàm số sau đây, hàm số nào không có cực trị 
	A. 	B. 	C. 	D. 
Câu 7: Số các giá trị thực của tham số m để đồ thị hàm số có tiệm cận ngang là:
	A. 3	B. 0	C. 1	D. 2
Câu 8: Cho mặt cầu (S) có tâm I và bán kính R = 8. Cắt mặt cầu bằng mặt phẳng (P) đi qua trung điểm của bán kính ta thu được thiết diện là một hình tròn. Tính bán kính r của hình tròn đó
	A. 	B. 	C. 	D. 
Câu 9: Cho hình chóp đều S.ABC có cạnh đáy là a, bán kính mặt cầu ngoại tiếp hình chóp đó là khi đó cạnh bên hình chóp là 
	A. 	B. 	C. 	D. 
Câu 10: Cho . Gía trị biểu thức 
	A. 	B. 7	C. 	D. 20
Câu 11: Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ dương
	A. 	B. 	C. 	D. 
Câu 17: Cho hàm số có đạo hàm . Số điểm cực trị của hàm số .
	A. 1	B. 4	C. 2	D. 3
Câu 18: Các giá trị của x thỏa mãn là:
	A. 	B. 	C. 	D. 
Câu 19: Bảng biến thiên sau là của hàm số nào trong bốn hàm số sau:
x
 0 1 
f’(x)
 0 + 0 0 +
f(x)
	A. 	B. 	C. 	D. 
Câu 20: Tìm m để hàm số nghịch biến trên khoảng .
	A. 	B. 	C. 	D. 
Câu 21: Cho hình chóp S.ABCD có đáy là hình chữ nhật với . Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng 450. Khi đó thể tích khối chóp S.ABCD là:
	A. 	B. 	C. 	D. 
Câu 22: Khối 20 mặt đều thuộc loại 
	A. 	B. 	C. 	D. 
Câu 23: Khi viết trong hệ thập phân có số các chữ số là n, khi đó n có giá trị là
	A. 1704	B. 204	C. 1024	D. 1824
Câu 24: Tập xác định của hàm số là:
	A. 	B. 	C. 	D. 
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình thang với hai cạnh đáy là AD và BC trong đó , AC cắt BD tại O, thể tích khối chóp S.OCD là , khi đó thể tích khối chóp S.ABCD là:
	A. 	B. 	C. 	D. 
Câu 26: Đường thẳng cắt đồ thị tại hai điểm phân biệt A, B. Khi đó diện tích tam giác OAB là:
	A. 2	B. 4	C. 6	D. 
Câu 27: Đặt . Hãy biểu diễn theo a, b? 
	A. 	B. 
	C. 	D. 
Câu 28: Trong các hàm số sau, hàm số nào đồng biến trên khoảng 
	A. 	B. 
	C. 	D. 
Câu 29: Tập xác định của hàm số là:
	A. 	B. 	C. 	D. 
Câu 30: Trong các mệnh đề sau, mệnh đề nào sai?
	A. Hình lăng trụ đều có các mặt bên là hình chữ nhật 
	B. Hình lăng trụ đều có tất cả các cạnh đều bằng nhau
	C. Hình lăng trụ đều có cạnh bên vuông góc với đáy
	D. Hình lăng trụ đều có các cạnh bên bằng đường cao của lăng trụ
Câu 31: Cho hàm số . Tìm tất cả các giá trị của tham số m để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục tung.
	A. 	B. 	C. 	D. 
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’ sao cho , mặt phẳng (A’B’C’) cắt cạnh SD tại D’, gọi lần lượt là thể tích của hai khối chóp S.A’B’C’D’; S.ABCD. Khi đó bằng:
	A. 	B. 	C. 	D. 
Câu 33: Tìm giá trị của tham số m để hàm số đồng biến trên :
	A. 	B. 	C. 	D. 
Câu 41: Cho và . Khẳng định nào sau đây đúng?
	A. 	B. 
	C. 	D. 
Câu 42: Cho hai số thực dương a, b và . Khẳng định nào sau đây là sai?
	A. 	B. 
	C. 	D. 
Câu 43: Đồ thị hàm số cắt trục hoành tại mấy điểm
	A. 2	B. 0	C. 3	D. 1
Câu 44: Số đường tiệm cận của đồ thị hàm số là:
	A. 1	B. 2	C. 3	D. 4
Câu 45: Tìm tham số m để đường thẳng cắt đồ thị hàm số tại 4 điểm phân biệt
	A. 	B. 	C. 	D. 
Câu 46: Cho hàm số . Tiệm cận ngang của đồ thị hàm số là:
	A. 	B. 	C. 	D. 
Câu 47: Cho hàm số . Các khoảng đồng biến của hàm số là:
	A. và 	B. và 
	C. và 	D. và 
Câu 48: Tập xác định của hàm số là:
	A. 	B. 	C. 	D. 
Câu 49: Cho đồ thị hàm số nhận là hai điểm cực trị, khi đó có giá trị là 
	A. 	B. 	C. 4	D. 
Câu 50: Các giá trị x thỏa mãn là:
	A. 4 và 	B. 2	C. 	D. 4
Đáp án
1-C
2-C
3-B
4-B
5-D
6-B
7-C
8-D
9-C
10-D
11-A
12-C
13-B
14-C
15-D
16-C
17-D
18-C
19-C
20-B
21-A
22-B
23-A
24-B
25-D
26-B
27-A
28-A
29-B
30-B
31-D
32-A
33-A
34-D
35-A
36-A
37-B
38-D
39-C
40-A
41-B
42-B
43-A
44-D
45-A
46-A
47-C
48-B
49-D
50-B
LỜI GIẢI CHI TIẾT
Câu 1: Đáp án C
- Phương pháp: Chú ý công thức tính diện tích toàn phần hình lăng trụ 
 ( trong đó các mặt bên hình lăng trụ tam giác đều là các hình chữ nhật bằng nhau; hai đáy là hai tam giác đều bằng nhau).
- Cách giải: Diện tích hai đáy hình lăng trụ là 
Diện tích mỗi mặt bên hình lăng trụ là 
Tổng diện tích ba mặt bên hình lăng trụ là 
Ta có diện tích toàn phần hình lăng trụ là 
Câu 2: Đáp án C
- Phương pháp: 
Nếu hàm số y có và thì x0 là điểm cực đại của hàm số.
- Cách giải: Ta có 
Nếu x=0 là điểm cực đại của hàm số. Để giá trị cực đại bằng 3 thì m>0 và
Nếu là điểm cực đại của hàm số. Để giá trị cực đại bằng 3 thì m<0 và
 không có giá trị m thỏa mãn
Câu 3: Đáp án B
- Phương pháp: 
Cách xác định góc giữa hai mặt phẳng 
+ Xác định giao tuyến chung của hai mặt phẳng 
+ Tìm hai đường thẳng nằm trên hai mặt phẳng sao cho cùng vuông góc với giao tuyến tại một điểm 
+ Góc giữa hai mặt phẳng là góc giữa hai đường thẳng trên.
Công thức tính thể tích khối chóp . Trong đó B là diện tích đáy, h là chiều cao.
- Cách giải: Gọi M là trung điểm của BC. Ta có (vì đều).
Mặt khác ta có (vì cân)
Giao tuyến của hai mặt phẳng (ABC) với (A’BC) là cạnh BC.
Suy ra góc giữa hai mặt phẳng (ABC) với (A’BC) là .
Xét tam giác đều nên 
Xét tam giác vuông tại A, ta có
Diện tích hình chữ nhật BCB’C’ là: 
Thể tích khối chóp ABCC’B’ là 
Câu 4: Đáp án B
- Phương pháp: Ta có 
Khi đó đồ thị hàm số là bao gồm đồ thị hàm số với , và đồ thị hàm số với .
Ngoài ra chú ý số nghiệm của phương trình chính bằng số giao điểm của đồ thị hàm số và đường thẳng 
- Cách giải: số nghiệm của phương trình chính bằng số giao điểm của đồ thị hàm số và đường thẳng .
Từ đồ thị ta giữ nguyên đồ thj hàm số với và lấy đối xứng phần đồ thị với qua trục oy. 
Vậy để phương trình có 3 nghiệm phân biệt thì .
Câu 5: Đáp án D
- Phương pháp: Từ đồ thị hàm số ta có thể chỉ ra tọa độ điểm thuộc đồ thị hàm số. Như thì giá trị x nằm trên trục hoành và giá trị y nằm trên trục tung.
Hàm số đồng biến thì đồ thị đi lên, nghịch biến đồ thị đi xuống.
- Cách giải: Từ đồ thị hàm số ta thấy:
Hàm số đồng biến trên 
Điểm cực đại của hàm số là 
Đồ thị đi qua điểm 
Đường thẳng y=2 cắt đồ thị hàm số tại 1 điểm
Câu 6: Đáp án B
- Phương pháp: Hàm số bậc 3 có cực trị khi y’=0 có hai nghiệm phân biệt 
Hàm số bậc 4 luôn có cực trị
- Cách giải: Vì hàm số bậc 4 luôn có cực trị nên loại A, C.
Hàm số 
y’ có 1 nghiệm nên hàm số không có cực trị suy ra chọn B.
Hàm số 
y’ có 2 nghiệm nên hàm số có cực trị suy ra loại D.
Câu 7: Đáp án C
- Phương pháp: Để hàm số có tiệm cận ngang thì phải tồn tại giới hạn hữu hạn tại vô cực của hàm số (tồn tại giới hạn hữu hạn hoặc 
- Cách giải: 
 . Để hàm số có giới hạn hữu hạn tại vô cực thì hệ số của x phải triệt tiêu 
+) suy ra hệ số của x là nên giới hạn này không hữu hạn.
+) suy ra hệ số của x là 
Với thay trở lại hàm số không xác định khi 
Với 
= 
Vậy có một giá trị thực của m để đồ thị hàm số có tiệm cận ngang
Câu 48: Đáp án B
- Phương pháp: 
Tập xác định của hàm số lũy thừa tùy thuộc vào giá trị của . Cụ thể
Với nguyên dương, tập xác định là 
Với nguyên âm hoặc bằng 0, tập xác định là 
Với không nguyên, tập xác định là 
- Cách giải: 
Hàm số có giá trị của , khi đó điều kiện xác định của hàm số là 
Tập xác định của hàm số là 
Câu 49: Đáp án D
- Phương pháp: +Tìm tọa độ hai cực trị 
+Tính 
- Cách giải: 
Câu 50: Đáp án B
- Phương pháp: Chú ý điều kiện tồn tại là 
Phương trình logarit cơ bản 
Các phương pháp giải phương trình mũ là 
+ Đặt ẩn phụ 
+ đưa về cùng cơ số 
+ logarit hóa
- Cách giải: 
Điều kiện 
Ta có 
Er89jaw890vr0w89j90c3rasdufcsetsdvj,ioptgjsdockfaw,-0tivaw390t4kq390ircq2crafsetgertb34tbawetbawe4tb ase4tasetb awertbaw ọoifjairf sdrfhsoefij siofjasepfkasopekfvasdiopjfiopsdjkfopsdkfsdopgjmopdf,vp[zxdgdbio pserk gsg SsfSDFSDfsdhfosu ioaasd iofjasmo efiwj iop
driotvuneioraw,opcioaeurymaeio[ctopwaemjtiovptgseriovyhut3490utiodfjh90rtf,gopdfghiojsdf pasdkjng fkc, wei9rtfng289034u90238491284901285902385903489058123490542390482390482390482390482390542390482390842390842353489ut5jgvdfmfgjkr23r4qwmfiopawje
eev awetb awtbawt4vbawe4ynw34n7w54q3b49tu8vq234094tvkq34-ivytse-0tv4ise-0tbikeraseopfasev rvaw3rawr