Đề thi thử nghiệm THPT QG - Môn Toán - Đề 20

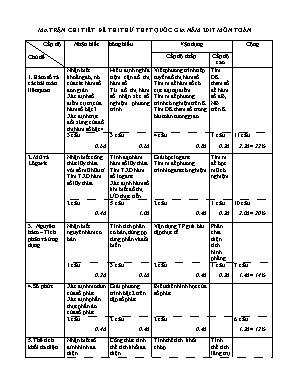
MA TRẬN CHI TIẾT ĐỀ THI THỬ THPT QUỐC GIA NĂM 2017 MÔN TOÁN
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
 Cấp độ thấp
Cấp độ cao
1. Hàm số và các bài toán liên quan
Nhận biết khoẳng đb, nb của các hàm số đơn giản.
Xác định số điểm cự trị của hàm số bậc 3
Xác định trục đối xứng của đồ thị hàm số bậc 4
Hiểu định nghĩa tiệm cận đồ thị hàm số
Từ đồ thị hàm số nhận xét số nghiệm phương trình
Viết phương trình tiếp tuyến đồ thị hàm số
Tìm m để hàm số có cực đại tại điểm
Tìm m để phương trình có nghiệm trên K
Tìm ĐK tham số trong bài toán tương giao
Tìm ĐK tham số để hàm số đB, NB trên K
3 câu
0.6đ
3 câu
0.6đ
4 câu
0.8đ
1 câu
0.2đ
11 câu
2.2đ = 22%
2. Mũ và Lôgarit 
Nhận biết công thức lũy thừa với số mũ hữu tỉ
Tìm TXĐ hàm số lũy thừa
Tính đạo hàm hàm số lũy thừa
Tìm TXĐ hàm số logarit
Xác định hàm số khi biết đồ thị
ƯD thực tiễn
Giải bpt logarit
Tìm m để phương trình logarit có nghiệm 
Tìm m để bpt mũ có nghiệm
2 câu
0.4đ
5 câu
1.0đ
2 câu
0.4đ
1 câu
0.2đ
10 câu
2.0đ = 20%
3. Nguyên hàm – Tích phân và ứng dụng
Nhận biết nguyên hàm cơ bản
Tính tích phân cơ bản, dùng pp từng phần và đổi biến
Vận dụng TP giải bài tập thực tế
Phân chia diện tích hình phẳng
1 câu
0.2đ
3 câu
0.6đ
2 câu
0.4đ
1 câu
0.2đ
7 câu
1.4đ = 14%
4. Số phức
Xác định modun của số phức
Xác định phần thực phần ảo của số phức
Giải phương trình bậc 2 trên tập số phức
Biểu diễn hình học của số phức
2 câu
0.4đ
2 câu
0.4đ
2 câu
0.4đ
6 câu
1.2đ = 12%
5. Thể tích khối đa diện
Nhận biết số đỉnh hình đa diện
Công thức tính thể tích khối đa diện
Tính thể tích khối chóp
Tính thể tích lăng trụ liên quan khoảng cách
1 câu
0.2đ
1 câu
0.2đ
1 câu
0.2đ
1 câu
0.2đ
4 câu
0.8đ = 8%
6. Khối tròn xoay
Công thức tính diện tích toàn phần hình trụ
Tính thể tích khối trụ
Tính diện tích xung quanh hình nón
Bài toán cực trị hình nón
1 câu
0.2đ
2 câu
0.4đ
1 câu
0.2đ
4 câu
0.8đ = 8%
7. Phương pháp tọa độ trong không gian
Viết phương trình mặt phẳng qua điểm và có vtpt
Viết pt mặt cầu biết tâm và bán kính
Tìm giao điểm đt và mp
Tính khoảng cách giữa hai mp song song
Tìm đk đt và mp vuông góc
Xác định điểm thỏa mãn tính chất 
Tìm điểm trên mp thỏa mãn tính chất
Viết phương trình mặt phẳng thỏa mãn nhiều yếu tố cho trước
2 câu
0.4đ
4 câu
0.8đ
1 câu
0.2đ
1 câu
0.2đ
8 câu
1.6đ = 16%
Tổng số câu: 50 
Tổng số điểm: 10
Số câu: 11
Số điểm: 2.2
22%
Số câu: 20
Số điểm: 4.0
40%
Số câu: 19
Số điểm: 3.8
38%
 KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2017
 	 MÔN THI: TOÁN 
 (Đề thi thử nghiệm) (Thời gian làm bài: 90 phút không kể thời gian giao đề)
Trong các hàm số sau đây, hàm số nào nghịch biến trên khoảng (-3;-2)
A. 	B. 	C. 	D. 
Hàm số : có bao nhiêu điểm cực trị ?
A. 2	B. 1	C. 0	D. 3
Đồ thị hàm số có trục đối xứng là đường thẳng có phương trình
A. B. C. D. 
Sốtiệmcậncủađồthịhàmsố y = x2+5-3x2+8x+15 là:
A. 1 B. 2 C. 3 D. 0
Đồthị ở hìnhsaulàđồthịcủahàmsốnào ?
A.B.y = x4 – 2x2 – 3 C.y = - x4 – 2x2 – 3 D.y = -x4 - 2x2 + 3
Cho đồthịcủahàmsố y = f(x). Tấtcảcácgiátrịcủa mphươngtrìnhcóbốnnghiệmlà: 
A. khôngcógiátrị m 	B.	C.	 D. 
Tiếptuyếncủađồthịhàmsố, tạiđiểm x=-2 songsongvớiđườngthẳng y=3x+1 là : 
A. y=3x+10 B. y=3x-10 C.y=-3x +3 	D.y=-3x+11
Giátrịm để hàm số đạt cực tiểu tại là: 
A. 	B.	C.	D. 
Tấtcảcácgiátrịcủa m để phương trình:
4sin6x+cos6x-cos4x-sin2x+m-4=0 có nghiệm thuộc π2 ; πlà: 
A. m≤2B. 74≤m≤0C. -34≤m≤14; m≠0D. 34≤m≤1
Đường thẳng (d): y = - x + m luôn cắt đồ thị hàm số y = tại hai điểm P, Q. Giá trị của m để đoạn thẳng PQ ngắn nhất là:
A.m= 1B. m = 3 C. m = -1 D. m=2 
Tấtcảcácgiátrịthựccủathamsốđểhàmsốnghịchbiếntrênkhoảnglà: 
A.
B.
C.
D.
Cho a làsốthựcdương. Biểuthứcviếtdướidạnglũythừavớisốmũhữutỉlà
A. B. C. D. 
Tậpxácđịnhcủahàmsố y = là
 A. R B. R \ C. 	 D. R\
Đạohàmcủahàmsố y = là
	A. 	 B. 
 C. 	D. 
Tậpxácđịnhcủahàmsốlà: 
A. (3;+) 	 B. ( ; 0)( 3 ; + ) 
C. 	 D. R\ ( 0 ; 3 )
Hìnhvẽbênlàđồthịcủahàmsố
A. 	 B. 
C. 	 D. 
Phươngtrìnhcónghiệm x bằng:
A. –3 	 B. –2 
 C. –1 	 D. 2
Mộtkhurừngcótrữlượnggỗướcchừngkhoảng 6.105 m3. Biếttốcđộsinhtrưởng ở khurừngđólà 5% mỗinăm. Sau 3 nămkhurừngđócósốmétkhốigỗướcchừnggầnnhấtvớigiátrịnàosauđây:
A.6,94575.105 B. 7,67548.105 	 C. 7,12545.105 	 D. 6,68325.105 
Tấtcảcácgiátrịcủa m đểphươngtrình: cónghiệmlà: 
A. B. C. D. 
Bấtphươngtrìnhcótậpnghiệmlà
A. 	 B. 
C. 	 D. 
Tấtcảcácgiátrịcủa mđểbấtphươngtrình: cónghiệmlà
A. B. C. D. 
Phátbiểunàosauđâylàđúng ?
A. B. 
C. D. 
Giátrịcủabằng:
A. 	B. 	C. 	D. 
Phátbiểunàosauđâylàđúng ?
A. B. 
C. D. 
Nếuđặtthìtíchphântrởthành:
A.	 B. 
C. D. 
Nếuvới a<d<b thìbằng:
A. -2 B. 8 C. 0 D. 3
Mộthồchứanướcchuẩnbịđượcbơmnướcvàođểtrữnướcphụcvụnôngnghiệp. Gọi h(t) là thểtíchnướcđượcbơmvàosau t giây. Chovàa, b làthamsố. Ban đầuhồkhôngcónước. Sau 5giâythìthểtíchnướctronghồlà. Sau 10giâythìthểtíchnướctronghồlà. Tínhthểtíchnướctronghồsaukhibơmđược 20 giây
A. B. C. D. .
Parabol y = chia hình tròn có tâm tại gốc tọa độ, bán kính thành 2 phần, Tỉ số diện tích của phần lớn và phần nhỏ thuộc khoảng nào:
A. 	B. 	C. 	D. 
Cho sốphức. Môđuncủasốphứczlà
A.
1
B.
C.
3
D.
9
Cho số phức z thỏa mãn: . Xác định phần thực và phần ảo của z.
A. Phần thực – 2 ; Phần ảo 5i.	B. Phần thực – 2 ; Phần ảo 5.
C. Phần thực – 2 ; Phần ảo 3.	D. Phần thực – 3 ; Phần ảo 5i.
Gọi z1, z2 là hai nghiệm phức của phương trình . Tính giá trị của biểu thức .
A. 15.	B. 17.	C. 19.	D. 20
Cho số phức z thỏa mãn: . Tìm môđun của .
A. 	B. 	C. 	D. 
Trong mp tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn:.
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2, –1), bán kính R=.
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, 1), bán kính R=.
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R=.
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R=.
Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn cho số phức z = 3 – 4i; M’ là điểm biểu diễn cho số phức . Tính diện tích tam giác OMM’.
A. .	B. 	C. 	D. 
Số đỉnh của hình 20 mặt đều là:
A. Mười hai	B. Mười sáu	C. Hai mươi	D. Ba mươi
Nếu một hình chóp đều có chiều cao và cạnh đáy cùng tăng lên 3 lần thì thể tích của nó tăng lên: 
A.18 lần 	B. 9 lần 	 C.27 lần 	D. 54 lần
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, biết , , SA(ABC) và . Thể tích khối chóp S.ABC là : 
A. 	B.	C.	 D. 
Cho lăng trụ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm lên mặt phẳng trùng với trực tâm tam giác . Biết khoảng cách giữa hai đường thẳng và bằng . Khi đó thể tích của khối lăng trụ là
A.	B. 	C. 	D. 
Gọilầnlượtlàđộdàiđườngsinh, chiềucaovàbánkínhđáycủahìnhtrụ (T). Diệntíchtoànphầncủahìnhtrụ (T) là
A.	B.	C.	D.
ThểtíchVcủakhốitrụcóchiềucaobằng a vàđườngkínhđáybằng là
A.	B.	C.	D.
Cho hìnhnóncóđườngsinhl, gócgiữađườngsinhvàmặtphẳngđáylà. Diệntíchxungquanhcủahìnhnónnàylà
A.	B.	C.	D.
Cho hìnhnóncóbánkínhđáybằng 10, mặtphẳngvuônggócvớitrụccủahìnhnóncắthìnhnóntheomộtđườngtròncóbánkínhbằng 6, khoảngcáchgiữamặtphẳngnàyvớimặtphẳngchứađáycủahìnhnónlà 5. Chiềucaocủahìnhnónlà
A.	B.	10	
C.	8,5	D.7
Cho đường thẳng đi qua điểm M(2;0;-1) và có vectơ chỉ phương 
Phương trình tham số của đường thẳng là:
A. 	B. 	C. 	D. 
Tìm giao điểm của và 
A. M(3;-1;0)	B. M(0;2;-4)	C. M(6;-4;3)	D. M(1;4;-2)
Mặt cầu (S) có tâm I(-1;2;1) và tiếp xúc với mặt phẳng (P): , phương trình là
A. 	B. 
C. 	D. 
Khoảngcáchgiữa 2 mặtphẳngvàlà: 
	A. 1	B. 	C.	D. 4
Cho đườngthẳng d vàmpvới,. Giátrịcủa m để d vuônggóclà: 
A. 	B. 	C. 	D. 
Trong không gian với hệ toạ độ 0xyz cho A(2;0;0); B(0;3;1); C(-3;6;4). Gọi M là điểm nằm trên cạnh BC sao cho MC = 2MB. Độ dài đoạn AM là:
A. 	B. 	C. 	D. 
TrongkhônggianvớihệtrụctọađộOxyz, chomặtphẳngvàcácđiểm, . Tọađộđiểmsaochonhỏnhất. 
A. 	B. 	C. 	D. 
TrongkhônggianvớihệtrụctọađộOxyz, chomặtphẳngvàđườngthẳng (d) . Mặtcầu (S) tâmthuộcđường d, tiếpxúc (P) vàcắt (Q)theođườngtròngiaotuyếncóchu vi là : 
A. 	B. 
C. 	D. 
ĐÁP ÁN ĐỀ THI THỬ THPT QUỐC GIA 2017
1B
2A
3C
4C
5A
6C
7A
8A
9D
10A
11C
12A
13B
14A
15B
16D
17C
18A
19C
20A
21A
22D
23A
24D
25C
26D
27A
28B
29B
30B
31D
32A
33D
34A
35A
36C
37D
38B
39A
40C
41A
42A
43B
44A
45B
46A
47A
48C
49D
50A