Đề thi thử môn Toán - Đề 5

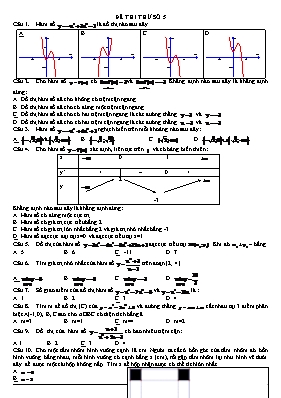
ĐỀ THI THỬ SỐ 5
Hàm số là đồ thị nào sau đây	
A
B
C
D
Cho hàm số có và . Khẳng định nào sau đây là khẳng định đúng:
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và .
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và .
Hàm số nghịch biến trên mỗi khoảng nào sau đây:
A. và	B. 	C. 	 D. 
Cho hàm số xác định, liên tục trên và có bảng biến thiên:
x
 0 1 
y’
 +
 – 0 +
y
 2 
 -3
Khẳng định nào sau đây là khẳng định đúng:
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 2.
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3.
D. Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1.
Đồ thị của hàm số đạt cực tiểu tại . Khi đó bằng 
A. 5	B. 6	C. -11	D. 7
Tìm giá trị nhỏ nhất của hàm số trên đoạn [2; 4].
A. 	B. 	C. 	D. 
Số giao điểm của đồ thị hàm số và là :	
A. 1	B. 2	C. 3	D. 4
Tìm m để đồ thị (C) của và đường thẳng cắt nhau tại 3 điểm phân biệt A(-1;0), B, C sao cho ΔOBC có diện tích bằng 8.
A. m=3	B. m=1	C. m=4	D. m=2 
Đồ thị của hàm số có bao nhiêu tiệm cận:
A.1	B. 2	C. 3	D. 4
Cho một tấm nhôm hình vuông cạnh 18 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
A. 
B. 
C. 
D. 
Tìm tất cả giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng :
A. 	 B. 	 C. 	D. 
Giải phương trình 
A. 	 B. 	 C. 101	 D. 
Tính đạo hàm của hàm số 
A. 	 B. 	 C. 	 D. 
Giải bất phương trình 
A. x = 0	 B. x 0	 D. 0 < x < 1
Tìm tập xác định của hàm số 
A. 	 B. 	 C. 	 D. 
Cho hàm số . Khẳng định nào sau đây sai :
A. B. 
C. D. 
Cho hệ thức . khẳng định nào sau đây là đúng ? 
A. 	 B. 
C. 	 D. 
Tính đạo hàm của hàm số 
A. 	B. C. 	D. 
Giả sử ta có hệ thức . Hệ thức nào sau đây đúng
A. 	 B. 
C. 	 D. 4
Cho . Khi đó Tính theo a và b 
A. 	 B. 	 C. a+b	D. 
Tìm nguyên hàm của hàm số 
A. B. 
 C. D. 
Một nguời gửi tiết kiệm với lãi suất 8,4% năm và lãi hàng năm đuợc nhập vào vốn, hỏi sau bao nhiêu tháng ngưòi đó thu đuợc gấp đôi số tiền ban đầu (lấy giá trị quy tròn) ? 
A. 96; 	 B. 97	 C. 98	D. 99
Công thức tính diện tích S của hình thang cong giới hạn bởi hai đồ thị (a<b) .
A. B. 
C. D. 
Giá trị m để hàm số F(x) =mx3 +(3m+2)x2-4x+3 là một nguyên hàm của hàm số là:
A. m = 3 B. m = 0 C. m = 1 D. m = 2
Tính tích phân 
	C. I =1	
Tính tích phân 
A. ;	B. ;	C. .	D. 
Diện tích hình phẳng giới hạn bởi đồ thị (C) của hàm số và đồ thị (C’) của hàm số bằng:
A. 0	B. 1	C. 2	D. 3
Cho hình (H) là hình phẳng giới hạn bởi đồ thị hàm số ,trục Ox và đường thẳng .Thể tích của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox bằng:
A. 	B. 	C. 	D. 
Cho số phức .Phần thực và phần ảo của số phức lần lượt là:
A.-3 và -7	B. 3 và -11 	C. 3 và 11	D. 3 và -7
Cho hai số phức .Môđun của số phức bằng:
A.5	B. 	C. 	D. 3
P
N
Q
M
 Cho số phức z thỏa mãn .Điểm nào sau đây biểu diễn cho z trong các điểm M,N,P,Q ở hình bên?
A. Điểm M	
B. Điểm N	
C. Điểm P	 	
D. Điểm Q
Cho số phức .Tìm số phức ?
A.	B. 	C. 	D. 
Gọi là bốn nghiệm phức của phương trình .Tổng bằng:
A.5	B. 	C. 	D. 
Cho các số phức z thỏa mãn .Biết rằng tập hợp các điểm biểu diễn các số phức là một đường tròn.Tính bán kính r của đường tròn đó.
A.20	B.	C.	D.7
Cho khối lăng trụ đứng ABC.A’B’C’,đáy ABC là tam giác vuông tại B,AB=BC=2a,AA’=.Tính thể tích khối lăng trụ ABC.A’B’C’.
A.	B.	C. 	D. 
Cho hình chop S.ABCD có đáy ABCD là hình chữ nhật ,AB=a,BC=2a,cạnh bên SA vuông góc với đáy và SA=.Tính thể tích khối chop S.ABCD.
A. 	B. 	C.	D. 
Cho khối tứ diện OABC với OA,OB,OC vuông góc từng đôi một và OA=a,OB=2a,OC=3a.Gọi M,N lần lượt là trung điểm của hai cạnh AC,BC.Thể tích của khối tứ diện OCMN tính theo a bằng:
A. 	B.	 C. 	D. 
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,SA vuông góc với đáy ,thể tích khối chóp bằng .Tính khoảng cách từ A đến mặt phẳng (SBD).
A. 	 B.	 C. 	D. 
Trong không gian cho tam giác ABC vuông tại A với AC=3a,AB=4a.Tính độ dài đường sinh l của hình nón nhận được khi quay tam giác ABC quanh trục AC.
A. 	 B.	 C. 	D. 
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, AB=AC=a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối cầu ngoại tiếp hình chóp S.ABC.
A. 	B. 	 C. 	D. 
Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Diện tích toàn phần của khối trụ là:
A. B. C. D.
Từ tấm tôn hình chữ nhật cạnh 90cm x 180cm người ta làm các thùng đựng nước hình trụ có chiều cao bằng 80cm theo 2 cách(Xem hình minh họa dưới) 
Cách 1. Gò tấm tôn ban đầu thành mặt xung quanh của thùng
Cách 2.Cắt tấm tôn ban đầu thành 3 tấm bằng nhau và gò các tấm đó thành mặt xung quanh của thùng . 
Ký hiệu là thể tích của thùng gò được theo cách thứ nhất và là tổng thể tích của ba thùng gò được theo cách thứ 2.Tính tỉ số 
A. 	 B.	 C. 3	 D.2
Trong không gian Oxyz, cho 3 điểm M(1;0;2), N(-3;-4;1), P(2;5;3). Phương trình mặt phẳng (MNP) là
A. 	B. 
C. 	D. 
Trong không gian Oxyz, cho mặt cầu (S) : , đường thẳng . Mặt phẳng (P) vuông góc với và tiếp xúc với (S) có phương trình là:
A. 	và 	B. và 
C. và 	D. 	và 
Trong không gian Oxyz, cho A(4;-2;3), , đường thẳng d đi qua A cắt và vuông góc có vectơ chỉ phương là
A. 	B. 	C. 	D. (3;0;-1)
Trong không gian Oxyz, cho 2 mặt phẳng (P) : x-y+4z-2=0 và (Q): 2x-2z+7=0. Góc giữa 2 mặt phẳng (P) và (Q) là:
A. 	B. 	C. 	D. 900
Trong không gian Oxyz, cho mặt phẳng 3x-y+z-4 =0 . mp cắt mặt cầu (S) tâm I(1;-3;3) theo giao tuyến là đường tròn tâm H(2;0;1) , bán kính r =2. Phương trình (S) là:
A. 	B. 
C. 	D. 
Trong không gian Oxyz, cho 2 điểm A(1;2;0), B(-2;3;1), đường thẳng . Tọa độ điểm M trên sao cho MA=MB là :
A. 	B. 	C. 	D. 
Đường thẳng d đi qua H(3;-1;0) và vuông góc với (Oxz) có phương trình là:
A. 	B. 	C. 	D. 
Trong không gian Oxyz, cho E(-5;2;3), F là điểm đối xứng với E qua trục Oy. Độ dài EF là:
A. 	B. 	C. 	D. 
-----------------------Hết -------------------------
LỜI GIẢI - HƯỚNG DẪN
Hàm số là đồ thị nào sau đây	
A
B
C
D
Cho hàm số có và . Khẳng định nào sau đây là khẳng định đúng ?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và .
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và .
HD: Định lí
 là tiệm cận ngang
 là tiệm cận đứng
Hàm số nghịch biến trên mỗi khoảng nào sau đây 
A. và	B. 	C. 	D. 
Cho hàm số xác định, liên tục trên R và có bảng biến thiên :
x
 0 1 
y’
 +
 – 0 +
y
 2 
 -3
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 2.
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3.
D. Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1
Đồ thị của hàm số đạt cực tiểu tại . Khi đó bằng 
A. 5	B. 6	C. -11	D. 7
HD: 
Tìm giá trị nhỏ nhất của hàm số trên đoạn [2; 4].
A. 	B. 	C. 	D. 
HD: Bấm mod 7
Số giao điểm của đồ thị hàm số và là :	
A. 1	B. 2	C. 3	D. 4
HD: Bấm máy tính ta được 3 giao điểm
Tìm m để đồ thị (C) của và đường thẳng cắt nhau tại 3 điểm phân biệt A(-1;0), B, C sao cho ΔOBC có diện tích bằng 8.
A. m=3	B. m=1	C. m=4	D. m=2 
HD: Thử bằng máy tính và được m=4
Đồ thị của hàm số có bao nhiêu tiệm cận
A.1	B. 2	C. 3	D. 4
HD: Thử bằng máy tính và được 3 tiệm cận là y=0; x=-1; x=3
Cho một tấm nhôm hình vuông cạnh 18 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
A. 
B. 
C. 
D. 
HD: Điều kiện: 
Bấm mod 7 và tìm được x=3
Cách khác: Áp dụng BĐT Côsi cho 3 số không âm 4x; 18-2x; 18-2x
Dấu “=” xảy ra khi 
Vậy: x=3 thì thể tích lớn nhất
Tìm tất cả giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng 
A. 	B. 	C. 	D. 
Giải : TXĐ : D = 
Đh : 
Hàm số đồng biến trên khoảng : 
Chọn D .
Giải phương trình 
A. 	B. 	C. 101	d. 
Giải : 
Pt Û .
Chọn C.
Tính đạo hàm của hàm số 
A. 	B. 	C. 	D. 
Giải : y’ = . Chọn B
Giải bất phương trình 
A. x = 0	B. x 0	D. 0 < x < 1
Giải : Bpt . Chọn B
Tìm tập xác định của hàm số 
A. 	B. 	C. 	D. 
Giải : . Chọn D 
Cho hàm số . Khẳng định nào sau đây sai :
A. 
B. 
C. 
D. 
HD : Logarit hoá hai vế theo cùng một cơ số. Chọn C
Cho hệ thức . khẳng định nào sau đây là đúng ? 
A. 	B. 
C. 	D. 
Giải : 
Ta có : 
 à chọn D
Tính đạo hàm của hàm số 
A. 	B. 	C. 	D. 
Hướng dẫn : Áp dụng công thức . à Chọn B
Giả sử ta có hệ thức . Hệ thức nào sau đây đúng
A. 	B. 
C. 	D. 4
HD: 
Cho . Khi đó Tính theo a và b 
A. 	B. 	C. a+b	D. 
HD:
Tìm nguyên hàm của hàm số 
 A; B; 
 C; D; 
HD: Tìm nguyên hàm của hàm số =
Một nguời gửi tiết kiệm với lãi suất 8,4% năm và lãi hàng năm đuợc nhập vào vốn, hỏi sau bao nhiêu tháng ngưòi đó thu đuợc gấp đôi số tiền ban đầu (lấy giá trị quy tròn) ? 
A. 96;	B. 97.	C. 98;	D. 99
HD: Một nguời gửi tiết kiệm với lãi suất 8,4% năm và lãi hàng năm đuợc nhập vào vốn, hỏi sau bao nhiêu tháng ngưòi đó thu đuợc gấp đôi số tiền ban đầu? 
Giải:
Gọi x là số tiền gửi ban đầu (x>0)
Do lãi suất 1 năm la 8,4% nên lãi suất tháng là 0,7%
Số tiền sau tháng đâu tiên là: 
Số tiền sau năm thứ 2 là: 
Số tiền sau năm thứ n là: 
Giả thiết 
Công thức tính diện tích S của hình thang cong giới hạn bởi hai đồ thị (a<b) 
A. B. 
C. D. 
Giá trị m để hàm số F(x) =mx3 +(3m+2)x2-4x+3 là một nguyên hàm của hàm số là:
 A; m = 3; B; m = 0; C; m = 1; D; m = 2
HD: Ta có 
Tính tích phân 
HD:Tính tích phân 
Tính tích phân 
A. ;	B. ;	C. .	D. 
HD: 
Diện tích hình phẳng giới hạn bởi đồ thị (C) của hàm số và đồ thị (C’) của hàm số bằng:
A. 0	B. 1	C. 2	D. 3
Giải: Chọn B
Cho hình (H) là hình phẳng giới hạn bởi đồ thị hàm số ,trục Ox và đường thẳng .Thể tích của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox bằng:
A. 	B. 	C. 	D. 
Giải: Chọn A
Cho số phức .Phần thực và phần ảo của số phức lần lượt là:
A.-3 và -7	B. 3 và -11 	C. 3 và 11	D. 3 và -7
Giải: Chọn C
Cho hai số phức .Môđun của số phức bằng:
A.5	B. 	C. 	D. 3
Giải: Chọn B
P
N
Q
M
 Cho số phức z thỏa mãn .Điểm nào sau đây biểu diễn cho z trong các điểm M,N,P,Q ở hình bên?
A. Điểm M	
B. Điểm N	
C. Điểm P	 	
D. Điểm Q
Giải: Chọn D	
Điểm biểu diễn cho z
Cho số phức .Tìm số phức ?
A.	B. 	C. 	D. 
Giải: Chọn A
Gọi là bốn nghiệm phức của phương trình .Tổng bằng:
A.5	B. 	C. 	D. 
Giải: Chọn C
Cho các số phức z thỏa mãn .Biết rằng tập hợp các điểm biểu diễn các số phức là một đường tròn.Tính bán kính r của đường tròn đó.
A.20	B.	C.	D.7
Giải: Chọn B
Đặt 
Bán kính của đường tròn là 
Cho khối lăng trụ đứng ABC.A’B’C’,đáy ABC là tam giác vuông tại B,AB=BC=2a,AA’=.Tính thể tích khối lăng trụ ABC.A’B’C’.
A.	B.	C. 	D. 
HD: V(dvtt)
Chọn đáp án A
Cho hình chop S.ABCD có đáy ABCD là hình chữ nhật ,AB=a,BC=2a,cạnh bên SA vuông góc với đáy và SA=.Tính thể tích khối chop S.ABCD.
A. 	B. 	C.	D. 
HD: V=
Chọn đáp án B
Cho khối tứ diện OABC với OA,OB,OC vuông góc từng đôi một và OA=a,OB=2a,OC=3a.Gọi M,N lần lượt là trung điểm của hai cạnh AC,BC.Thể tích của khối tứ diện OCMN tính theo a bằng:
A. 	B.	C. 	D. 
HD: 
 (dvtt)
Chọn đáp án D
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,SA vuông góc với đáy ,thể tích khối chóp bằng .Tính khoảng cách từ A đến mặt phẳng (SBD).
A. 	B.	C. 	D. 
HD: 
Gọi 
Ta có:
Kẻ 
Hay AH=d(A;(SBD))
Vậy: d(A;(SBD))= 
Chọn đáp án A
Trong không gian cho tam giác ABC vuông tại A với AC=3a,AB=4a.Tính độ dài đường sinh l của hình nón nhận được khi quay tam giác ABC quanh trục AC.
A. 	B.	C. 	D. 
HD: Độ dài đường sinh l=
Chọn đáp án D
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, AB=AC=a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối cầu ngoại tiếp hình chóp S.ABC.
	A. 	B. 	C. 	D. 
HD: Gọi H là trung điểm của AB,G là trọng tâm của tam giác đều SAB=>G là tâm đường tròn ngoại tiếp tam giác SAB
Gọi O là tâm đường tròn ngoại tiếp tam giác vuông ABC=>O là trung điểm của CB
Qua O dựng đường thẳng d vuông góc với mp(ABC)=>d //SH
Qua G dựng đường thẳng vuông góc với mp(SAB) cắt d tại I,ta có :IA=IB=IC=ID=R
=>R là bán kính mặt cầu ngoại tiếp hình chóp .
Ta có: IO=GH=,OB=
R=IB=
Vậy thể tích khối cầu ngoại tiếp hình chóp : V=
Chọn đáp án D
Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Diện tích toàn phần của khối trụ là:
A. B. C. D.
HD: Thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng 3a
Ta có : l=h=2r=3a
Diện tích toàn phần của khối trụ là: S=
Chọn đáp án B
Từ tấm tôn hình chữ nhật cạnh 90cm x 180cm người ta làm các thùng đựng nước hình trụ có chiều cao bằng 80cm theo 2 cách(Xem hình minh họa dưới) 
Cách 1. Gò tấm tôn ban đầu thành mặt xung quanh của thùng
Cách 2.Cắt tấm tôn ban đầu thành 3 tấm bằng nhau và gò các tấm đó thành mặt xung quanh của thùng . 
Ký hiệu là thể tích của thùng gò được theo cách thứ nhất và là tổng thể tích của ba thùng gò được theo cách thứ 2.Tính tỉ số 
A. 	B.	C. 3	D.2
HD: Vì các thùng đều có chung chiều cao nên:
+)Diện tích đáy 1:
	Chu vi đáy 1: =180=>=
	=
+)Diện tích đáy 1: 
	Chu vi đáy 1: =60=>=
	==>3=
Vậy =3
Chọn đáp án C
Trong không gian Oxyz, cho 3 điểm M(1;0;2), N(-3;-4;1), P(2;5;3). Phương trình mặt phẳng (MNP) là
A. 	B. 
C. 	D. 
HD: (MNP) nhận làm VTPT và đi qua M(1;0;2) nên có pt:
 1(x-1)+3y-16(z-2)=0 giải được đáp án B
* Có thể dùng máy tính thay M,N,P vào các đáp án để thử
Trong không gian Oxyz, cho mặt cầu (S) : , đường thẳng . Mặt phẳng (P) vuông góc với và tiếp xúc với (S) có phương trình là:
A. 	và 	B. và 
C. và 	D. 	và 
HD: 
(P) nhận làm VTPT => pt (P) có dạng: 2x-2y+z+D=0
 (S) có tâm I(1;-2;1), bán kính R=3
 (P) tiếp xúc (S) => giải được D=2, D=-16 => Đáp án A
Trong không gian Oxyz, cho A(4;-2;3), , đường thẳng d đi qua A cắt và vuông góc có vectơ chỉ phương là
A. 	B. 	C. 	D. (3;0;-1)
HD:
Gọi M(2+3t;4;1-t) = (t). (3t-2;6;-2-t), (3;0;-1)
 Giả thiết => giải được t==> d có VTCP là Đáp án C
Trong không gian Oxyz, cho 2 mặt phẳng (P) : x-y+4z-2=0 và (Q): 2x-2z+7=0. Góc giữa 2 mặt phẳng (P) và (Q) là
A. 	B. 	C. 	D. 900
HD: (P) có VTPT ; (Q) có VTPT 
 Cos((P),(Q)) = => góc cần tìm là 600 => Đáp án A
Trong không gian Oxyz, cho mặt phẳng 3x-y+z-4 =0 . mp cắt mặt cầu (S) tâm I(1;-3;3) theo giao tuyến là đường tròn tâm H(2;0;1) , bán kính r =2. Phương trình (S) là
A. 	B. 
C. 	D. 
HD: (S) có bán kính R= => đáp án B
Trong không gian Oxyz, cho 2 điểm A(1;2;0), B(-2;3;1), đường thẳng . Tọa độ điểm M trên sao cho MA=MB là 
A. 	B. 	C. 	D. 
HD: Gọi M(1+3t;2t;t-2) . Giả thiết=> MA=MB => Đáp án A
* Có thể dùng máy tính thử các đáp án xem MA=MB ?
Đường thẳng d đi qua H(3;-1;0) và vuông góc với (Oxz) có phương trình là
A. 	B. 	C. 	D. 
HD: Dể thấy đáp án B
Trong không gian Oxyz, cho E(-5;2;3), F là điểm đối xứng với E qua trục Oy. Độ dài EF là
A. 	B. 	C. 	D. 
HD: F đối xứng qua Oy=> F(0 ;2 ;0) => EF=: Đáp án D
-----------------------Hết -------------------------