Đề thi thi thử số 02 môn Toán

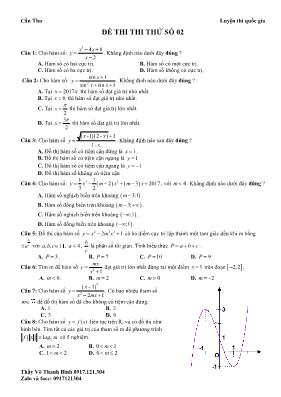
Cần Thơ Luyện thi quốc gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
ĐỀ THI THI THỬ SỐ 02 
Câu 1: Cho hàm số: 
3 4 8
2
x x
y
x
 


. Khẳng định nào dưới đây đúng ? 
A. Hàm số có hai cực trị. B. Hàm số có một cực trị. 
C. Hàm số có ba cực trị. D. Hàm số không có cực trị. 
 Câu 2: Cho hàm số: 
2
sin 1
sin sin 1
x
y
x x


 
. Khẳng định nào dưới đây đúng ? 
A. Tại 2017x  thì hàm số đạt giá trị nhỏ nhất. 
B. Tại 0x  thì hàm số đạt giá trị nhỏ nhất. 
C. Tại 
2
x

 thì hàm số đạt giá trị lớn nhất. 
D. Tại 
3
2
x

 thì hàm số đạt giá trị lớn nhất. 
Câu 3: Cho hàm số 
  -1 2 - 1
1-
x x
y
x

 . Khẳng định nào sau đây đúng ? 
A. Đồ thị hàm số có tiệm cận đứng là 1x  . 
B. Đồ thị hàm số có tiệm cận ngang là 1y  
C. Đồ thị hàm số có tiệm cận ngang là 1y   
D. Đồ thị hàm số không có tiệm cận 
Câu 4: Cho hàm số:    3 2
1 1
2 3 2017
3 2
y x m x m x      , với 4m  . Khẳng định nào dưới đây đúng ? 
A. Hàm số nghịch biến trên khoảng  3;1m . 
B. Hàm số đồng biến trên khoảng  3;m  . 
C. Hàm số nghịch biến trên khoảng  ;1 . 
D. Hàm số đồng biến trên khoảng  ;1 . 
Câu 5: Đồ thị của hàm số 4 2 22 1y x m x   có ba điểm cực trị lập thành một tam giác đều khi m bằng 
b
ca với , ,a b c , 4a  , 
b
c
 là phân số tối giản. Tính biểu thức P a b c   . 
A. 3P  . B. 7P  C. 10P  D. 9P  
Câu 6: Tìm m để hàm số 
2 1
mx
y
x


 đạt giá trị lớn nhất đúng tại một điểm 1x  trên đoạn  2;2 . 
 A. 0m  . B. 2m  C. 0m  D. 2m   
Câu 7: Cho hàm số 
 
2
2
1
2 1
x
y
x mx


 
. Có bao nhiêu tham số 
m để đồ thị hàm số đã cho không có tiệm cận đứng. 
 A. 1. B. 2 
 C. 3 D. 0 
Câu 8: Cho hàm số ( )y f x liên tục trên R, và có đồ thị như 
hình bên. Tìm tất cả các giá trị của tham số m để phương trình 
  2logf x m có 5 nghiệm. 
 A. 2m  . B. 0 1m  
 C. 1 2m  D. 0 2m  
Cần Thơ Luyện thi quốc gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
Câu 9: Một chuyến xe bus có sức chứa tối đa là 60 hành khách. Nếu một chuyến xe chở được x hành 
khách thì giá mỗi hành khách là 
2
1000 3
40
x 
 
 
 đồng. Tính số hành khách trên xe để thu được số tiền lớn 
nhất ? 
A. 50 khách. B. 40 khách. C. 55 khách. D. 42 khách. 
Câu 10: Cho hai điểm M, N di động trên đồ thị hàm số 
2 6
4
x
y
x



, MN đi qua (0;1)A . Tìm khoảng cách 
ngắn nhất từ điểm M đến điểm N. 
A. 2 . B. 3 C. 5 D. 7 
Câu 11: Cho hàm số 
3 1
3
x
y
x



 có đồ thị là (C). Điểm  0 0;M x y thuộc nhánh bên phải của đồ thị (C). Giá 
trị 
0 0x y bằng bao nhiêu nếu khoảng cách từ điểm M đến tiệm cận đứng bằng hai lần khoảng cách từ 
điểm M đến tiệm cận ngang của đồ thị hàm số. 
A. 0 0 2x y   . B. 0 0 5x y  C. 0 0 5x y   D. 0 0 2x y  
Câu 12: Tìm tập xác định D của hàm số:    
cot tan
2 21 1
x x
y x x    . 
A. D . B. D  \ 2k  , k . 
C. D    1;1 \ 2k   , k . D. D    1;1 \ k  , k . 
 Câu 13: Tính đạo hàm của hàm số:  log 2 1xy x  . 
A. 
2
2x 1
y 

. B. 
 
2
2 1 ln
y
x x
 

C. 
   
  2
2 ln 2 1 ln 2 1
2 1 ln
x x x x
y
x x x
  
 

 D. 
 
2
ln 2 1ln
2x 1
ln
xx
xy
x


  
 Câu 14: Khẳng định nào dưới đây sai ? 
A. Nếu 0x  thì 2018log 2018logx x . B. Nếu 0x  thì  2018log 2018logx x  . 
C. Nếu 0x  thì 2018log 2018logx x . D. Nếu 0x  thì 2018log x không có nghĩa. 
 Câu 15: Cho phương trình 
2 2 22 4.2 2 4 0x mx x mx mx     , với 
1
0;
2018
m
 
 
 
. Giả sử phương trình đã cho 
có ba nghiệm 1 2 3x x x  . Tính giá trị 1 2 3P x x x  . 
A. 0P  . B. 1P  C. P m D. 2P m 
Câu 16: Tìm tập nghiệm S của bất phương trình sau:  3 1
3
1
log log 2 1 1 0
2
x x    . 
 A. 
1
0;
2
S
 
 
 
. B.  0;2S C.  1;S  D.  0;4S 
Câu 17: Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức 1,05% . Theo số liệu của Tổng Cục 
Thống Kê, dân số của Việt Nam năm 2014 là 90.728.900 người. Với tốc độ tăng dân số như thế thì vào 
năm 2030 thì dân số của Việt Nam là bao nhiêu? 
A. 107232573 người. B. 107232574 người. 
C. 105971355 người. D. 106118331 người. 
Câu 18: Tìm tất cả các giá trị của tham số m để hàm số   2
1
1 ln
2
y m x mx x    đạt cực tiểu tại 1x  . 
 A. 1m  . B. 1m  C. 2m  D. 2m  
Cần Thơ Luyện thi quốc gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
Câu 19: Cho phương trình    
2 9x
x m x m   , với  , 1;2x m m  . Phương trình đã cho có bao nhiêu 
nghiệm ? 
 A. 3 . B. 2 C. 1 D. Vô số nghiệm 
Câu 20: Cho ,x y thỏa 1x y m   và 
2
4 .2 2x y xy m   . Nếu ,x y tồn tại thì m bằng bao nhiêu ? 
 A. 1m  . B. 2m  C. 0m  D. 3m   
Câu 21: Cho , ,x y z thỏa 
2 3
3 5
7 2
x
y
z
 




. Khẳng định nào dưới đây đúng ? 
A. 
140
2 1
log 63
1
xz
xyz z


 
. B. 
140
2
log 63
1
xz
xyz z


 
C. 
140
2 1
log 63
2 1
xz
xyz z


 
 D. 
140
1
log 63
2 1
xz
xyz z


 
 Câu 22: Cho hàm số 
  
1
( )
2 3
f x
x x m

 
, (giả sử m là hằng số và ( )f x có nghĩa ). Hãy tìm ( )F x 
dưới đây là một nguyên hàm của ( )f x . 
A. 
1 3
( ) ln
6 2
x m
F x
m x


 
. B. 
1 3
( ) ln
6 2
x m
F x
m x


 
. 
C. 
1 2
( ) ln
6 3
x
F x
m x m


 
. D. 
1 2
( ) ln
6 3
x
F x
m x m


 
. 
Câu 23: Cho tích phân  
1
0
3 xI x e dx a be    , với ,a b , Tính biểu thức    log
a b
P a b a b

    . 
. A. 2P  . B. 1P  C. 7 log7P   D. 1 log7P   
Câu 24: Cho tích phân 
2
0
cos 1 3sinI x xdx

  . Nếu đặt 1 3sint x  thì khẳng định nào dưới đây sai ? 
A. Do 21 3sin 1 3sint x t x     thì 
2
cos
3
tdt xdx . 
B. 
2
2
1
2
3
I t dt  . 
C. 
2
3
1
2
9
I t . 
D. 
14
9
I  . 
Câu 25: Một chiếc xe ôtô đang chuyển động với vận tốc ban đầu là  0 /v m s thì đạp phanh. Sau khi đạp 
phanh ôtô chuyển động chậm dần đều với vận tốc    25 2 /v t t m s  , trong đó t là khoảng thời gian 
được tính bằng giây, kể từ lúc bắt đầu đạp phanh đến khi dừng hẳn ôtô còn di chuyển được 156,25 mét. 
Hỏi vận tốc ban đầu của ôtô là bao nhiêu? 
 A.  0 20 /v m s . B.  0 25 /v m s 
C.  0 30 /v m s D.  0 35 /v m s 
Cần Thơ Luyện thi quốc gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
Câu 26: Cho đường thẳng y mx  và parabol 22y x  . Nếu diện tích hình phẳng giới hạn bởi hai 
đường kể trên bằng 
9
2
 (đvdt) thì khẳng định nào dưới đây đúng ? 
 A. 1m  . B. 2m  C. 2m   D. 1m   
Câu 27: Cho hàm số 1y x  . Diện tích hình phẳng S giới hạn bởi đồ 
thị của hàm số đã cho, trục tung và 3x  là phần tô đậm trong hình bên. 
Gọi V là thể tích khối tròn xoay được sinh bởi S khi quay quanh Ox . 
Hệ thức nào dưới đây đúng ? 
 A. 28 45V S  . B. 45 28V S  
C. 28 45V S D. 45 28V S 
Câu 28: Cho tích phân 
2
22
2
0 1
x a c
I dx
b dx
  

 , với , , ,a b c d ; ,
a c
b d
 là các phân số tối giản. Tính 
biểu thức 9a 5P b c d    . 
 A. 2P  . B. 3P  C. 19P   D. 8P   
Câu 29: Cho số phức z thỏa 2z . 2 5i z i   . Hỏi phần ảo của số phức z là bao nhiêu ? 
 A. 4i . B. 4 C. 4 D. 4i 
 Câu 30: Tính môđun của số phức z , biết 
2018
7 8 9 20...
1
i i i i
z
i
    
  
 
. 
A. 2018z  . B. 0z  C. 1z  D. 13z  
 Câu 31: Cho phương trình 2 0z Az B   có nghiệm bằng 
   
 
8
7
1 1 2
1
i i
z
i
  


, biết ,A B . Tính biểu 
thức 2P A B AB   . 
A. 124P  . B. 100P  C. 235P  D. 4P  
Câu 32: Cho các số phức z thỏa 2 2z i z z i    và được biểu diễn trong mặt phẳng phức thành đường 
parabol (P). Đường thẳng : 1d y x  tiếp xúc với (P) tại điểm M . Điểm M được biểu diễn thành số phức 
w. Tính môđun số phức w. 
A. w 3 . B. w 13 C. w 1 D. w 5 
Câu 33: Trong một mặt phẳng phức giả sử điểm M và M  theo thứ tự là các điểm biểu diễn của số phức 
, 'z z thỏa 
 
0
2 1
z
z i z


  
. Với O là gốc tọa độ thì khẳng định nào dưới đây đúng ? 
A. Tam giác OMM  vuông cân tại O. B. Tam giác OMM  vuông cân tại M  . 
C. Tam giác OMM  vuông cân tại M . D. Tam giác OMM  đều. 
Câu 34: Gọi V là thể tích của khối hộp . ' ' ' 'ABCD A B C D và 1V là thể tích của khối tứ diện có cùng đáy 
và chiều cao với khối hộp. Hệ thức nào sau đây đúng ? 
A. 16V V . B. 15V V . C. 14V V . D. 13V V . 
Câu 35: Mặt phẳng (P) cắt mặt cầu có tâm O theo đường tròn có bán kính bằng 4cm và khoảng cách từ O 
đến mp(P) bằng 3cm. Bán kính của mặt cầu là: 
A. 3 3 cm B. 5cm C. 3 2 cm D. 6cm 
Câu 36: Cho khối nón đỉnh S có đường sinh có dộ dài bằng a, góc giữa đường sinh và đáy là α. Thể tích 
của khối nón bằng 
Cần Thơ Luyện thi quốc gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
A. B. 
C. D. 
Câu 37: Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, ,AC a 060ACB  . 
Đường chéo BC' của mặt bên (BB'C'C) tạo với mặt phẳng  ' 'mp AA C C một góc 300. Tính thể tích V của 
khối lăng trụ theo a là: 
A. 3
4 6
3
V a . B. 3
6
3
V a . C. 3
2 6
3
V a . D. 3 6V a . 
Câu 38: Tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau; OA = a, OB = b, OC = c. Bán kính 
mặt cầu ngoại tiếp tứ diện là 
A . 
2 2 2a b c  B. 
2 2 2
2
a b c 
C. 
2 2 2
3
a b c 
 D. 
2 2 2
4
a b c 
Câu 39: Cho hình trụ có các đáy là hai hình tròn tâm O và O’, đường kính d đáy gấp đôi chiều cao h. Trên 
đường tròn tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Tính thể tích khối tứ diện OO’AB biết 
rằng 2 cmAB d  . 
 A. 
 64 2 5
125

. B. 
 125 2 5
64

 . C. 
 64 5 2
125

 . D.
 125 5 2
64

. 
Câu 40: Cho hình chữ nhật ABCD như hình vẽ bên. Nữa đường tròn bên có 
bán kính R. Tính diện tích S lớn nhất có thể của hình chữ nhật ABCD. 
 A. 22S R . B. 
2
2
R
S  . 
 C. 
22S R . D. 2S R . 
Câu 41: Cho hình nón có đường cao gấp hai lần bán kính đáy của nó. Tính tỉ số thể tích của khối cầu ngoại 
tiếp và nội tiếp của hình nón nói trên. 
A. 3
2 3
 cm
3
. B. 3
3
 cm
12
 . C. 3
3
 cm
6
. D. 3
3 3
 cm
8
. 
Câu 42: Trong không gian Oxyz, cho điểm  1;2;3M . Điểm nào dưới đây là điểm đối xứng với M qua 
trục Oy. 
A.  0;2;0A . B. 
1 3
;2;
2 2
B
 
 
 
 . C.  1;2; 3C   . D.
1 3
;2;
2 2
D
 
  
 
. 
Câu 43: Trong không gian Oxyz, cho tứ diện đều ABCD với  
1 3 1 3
1;0;0 , ; ;0 , ; ;0
2 2 2 2
A B C
   
        
   
. 
Khẳng định nào dưới đây đúng? 
 A. D Ox . B. D Oy . C. D Oz . D.  D Oxy . 
Câu 44: Trong không gian Oxyz, giả sử vectơ      ; 1;1 , 2; 1;0 , 3;0;2a a b b c      . Nếu a b và 
2
ac b thì 2 2a b bằng bao nhiêu ? 
 A. 2 . B. 1 . C. 0 . D.3 . 
3 21 .cos sin
3
a   3 2.cos sina  
3 21 .cos sin
2
a   3 2
1
.cos sin
6
a  
Cần Thơ Luyện thi quốc gia 
Thầy Võ Thanh Bình 0917.121.304 
Zalo và face: 0917121304 
Câu 45: Trong không gian Oxyz, cho hai điểm A B(2;1;3), (1; 2;1) và đường thẳng 
x t
d y t
z t
1
: 2
3 2
   


   
. Một 
mặt phẳng (P) đi qua hai điểm A, B và song song với d. Mặt phẳng (P) nhận vectơ nào dưới đây làm vectơ 
pháp tuyến của nó ? 
A.  n 10;4;1 B.   n 10; 4;1 C.   n 10;4; 1 D.    n 10; 4; 1 
Câu 46: Trong không gian Oxyz, cho mặt cầu (S): x y z x y2 2 2 2 4 4 0      và mặt phẳng (P):
x z 3 0   . Mặt phẳng nào dưới đây đi qua điểm M(3;1; 1) vuông góc với mặt phẳng (P) và tiếp xúc 
với mặt cầu (S). 
A.    x y z4 7 4 9 0 B.    x y z2 2 7 0 
C.    x y z2 2 7 0 D. x y z4 7 4 9 0    
Câu 47: Trong không gian Oxyz, cho đường thẳng 
x y z
d
1 1 2
:
2 1 3
  
  và mặt phẳng P : 
x y z 1 0    . Viết phương trình đường thẳng  đi qua A(1;1; 2) , song song với mặt phẳng P( ) và 
vuông góc với đường thẳng d . 
A.
  

 
   
2
: 5
3 2
x t
y t
z t
 B. 
  

 
   
1 2
: 1 5
2 3
x t
y t
z t
 C. 
  

 
  
2
: 5
3 2
x t
y t
z t
 D. 
  

 
  
1 2
: 1 5
2 3
x t
y t
z t
Câu 48: Trong không gian Oxyz, cho đường thẳng 
  

  
  
: 1 2
2
x t
y t
z t
, ( t R ) và mặt phẳng (P): 
x y z2 2 3 0    . Đường thẳng d nămg trong (P), cắt và vuông góc với  . Điểm nào dưới đây thuộc 
đường thẳng d ? 
A.  1;0;1A B.  1;1; 3B C.  1; 3;1C D.  1; 3;0D 
Câu 49: Trong không gian Oxyz, cho mặt phẳng ( ) : 2x 2 4 0P y z    và điểm  1;2;3A . Một mặt cầu 
(S) có tâm là A, cắt mặt phẳng (P) theo một thiết diện là hình tròn có chu vi bằng 8 . Tính bán kính của 
mặt cầu (S). 
 A. 5 B. 4 C. 6 D. 28 
Câu 50: Trong không gian Oxyz, cho ba điểm      2;0;0 , 0;2;0 , 0;0;2A B C . Một mặt cầu (S) nội tiếp tứ 
diện OABC, (O là gốc tọa độ). Tính bán kính R của mặt cầu (S). 
 A.   R 1 3 3
3
 B.   R 4 3 3
3
 C. 

R
2
3 3
 D. 

R
3
3 3
-------------------------------------Hết-------------------------------------