Đề thi olympic môn Toán Lớp 6 - Năm học 2014-2015 (Có đáp án)

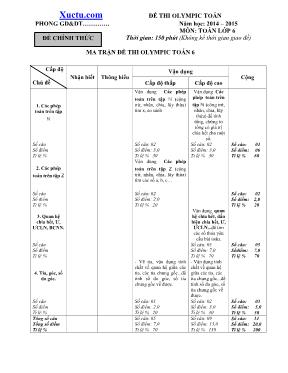
Xuctu.com ĐỀ THI OLYMPIC TOÁN 
 PHONG GD&DT. Năm học: 2014 – 2015 
 MÔN: TOÁN LỚP 6 
Thời gian: 150 phút (Không kể thời gian giao đề) 
MA TRẬN ĐỀ THI OLYMPIC TOÁN 6 
Vận dụng Cấp độ 
Chủ đề 
Nhận biết Thông hiểu 
Cấp độ thấp Cấp độ cao 
Cộng 
1. Các phép 
toán trên tập 
ℕ 
 Vận dụng Các phép 
toán trên tập ℕ (cộng 
trừ, nhân, chia, lũy thừa) 
tìm x, so sánh 
Vận dụng Các 
phép toán trên 
tập ℕ (cộng trừ, 
nhân, chia, lũy 
thừa) để tính 
tổng, chứng tỏ 
tổng có giá trị 
chia hết cho một 
số. 
Số câu 
Số điểm 
Tỉ lệ % 
 Số câu: 02 
Số điểm: 3,0 
Tỉ lệ % 30 
Số câu: 02 
Số điểm: 3,0 
Tỉ lệ % 30 
Số câu: 04 
Số điểm: 06 
Tỉ lệ % 60 
2. Các phép 
toán trên tập Z 
Vận dụng Các phép 
toán trên tập Z (cộng 
trừ, nhân, chia, lũy thừa) 
tìm các số a, b, c 
Số câu 
Số điểm 
Tỉ lệ % 
 Số câu: 02 
Số điểm: 2,0 
Tỉ lệ % 20 
 Số câu: 02 
Số điểm: 2,0 
Tỉ lệ % 20 
3. Quan hệ 
chia hết, Ư, 
ƯCLN, BCNN. 
 Vận dụng quan 
hệ chia hết, dấu 
hiệu chia hết, Ư, 
ƯCLN...để tìm 
các số thỏa yêu 
cầu bài toán. 
Số câu 
Số điểm 
Tỉ lệ % 
 Số câu: 05 
Số điểm: 7,0 
Tỉ lệ % 70 
Số câu: 05 
Sốđiểm: 7,0 
Tỉ lệ % 70 
4. Tia, góc, số 
đo góc. 
 - Vẽ tia, vận dụng tính 
chất về quan hệ giữa các 
tia, các tia chung gốc...để 
tính số đo góc, số tia 
chung gốc vễ được. 
- Vận dụng tính 
chất về quan hệ 
giữa các tia, các 
tia chung gốc...để 
tính số đo góc, số 
tia chung gốc vễ 
được. 
Số câu 
Số điểm 
Tỉ lệ % 
 Số câu: 01 
Số điểm: 2,0 
Tỉ lệ % 20 
Số câu: 02 
Số điểm: 3,0 
Tỉ lệ % 30 
Số câu: 03 
Số điểm: 5,0 
Tỉ lệ % 50 
Tổng số câu 
Tổng số điểm 
Tỉ lệ % 
 Số câu: 05 
Số điểm: 7,0 
Tỉ lệ % 70 
Số câu: 09 
Số điểm: 13,0 
Tỉ lệ % 130 
Số câu: 14 
Số điểm: 20,0 
Tỉ lệ % 200 
ĐỀ CHÍNH THỨC 
UBND HUYỆN  ĐỀ THI OLYMPIC TOÁN 
 PHONG GD&DT. Năm học: 2014 – 2015 
 MÔN: TOÁN LỚP 6 
Thời gian: 150 phút (Không kể thời gian giao đề) 
 Câu 1: (6,0 điểm) 
a) Cho 
7
2013
7
2012
7
2015
7
2014
7
2015
4
2014
4
2013
4
2012
4
4


A và 
22
2...221
2015
20132


B 
 Tính A – B. 
b) Tìm x biết (x + 1) + (x + 2) + (x + 3) + ... + (x + 100) = 5750. 
c) Cho C = 3 + 32 + 33 + 34 + 3100 chứng tỏ C chia hết cho 40. 
d) Tính tổng: S = 
92 2
3
...
2
3
2
3
3  
Câu 2: (4,5 điểm) 
a) Tìm số x có chữ số tận cùng bằng 2, biết rằng x, 2x, 3x đều là các số có 3 chữ 
số và 9 chữ số của 3 số đó đều khác nhau và khác 0. 
b) Tìm số tự nhiên nhỏ nhất, biết rằng số đó khi chia cho 3, cho 4, cho 5, cho 6 đều dư 
là 2, còn chia cho 7 thì dư 3. 
 c) Tìm hai số tự nhiên biết tổng ƯCLL và BCNN của chúng bằng 23 
 Câu 3: (4,5 điểm) 
 a) Tìm a, b, c biết: a – b = 2013 ; b – c = –2014 ; c + a = 2015 
 b) Tìm hai số tự nhiên m và n biết : BCNN(m,n)=180; ƯCLN(m,n) = 12. 
 c) Tìm số nguyên dương n để P = 
2
1
n
n
 

 là số nguyên. 
d) So sánh (–2)3333 và (–3)2222 
Câu 4: (5,0 điểm) Cho 4 tia chung gốc theo thứ tự Ox, Oy, Oz, Ot sao cho 
1
2
xOy zOt   ; 
1
2
yOz xOy   , biết số đo góc zOt bằng 600. 
a) Tính số đo các góc xOy; yOz; tOx? 
b) Vẽ tia Om sao cho số đo góc mOt bằng 200 . Tính số đo góc zOm? 
c) Vẽ thêm 2010 tia phân biệt chung gốc với các tia Ox, Oy, Oz, Ot, Om. Hỏi có 
bao nhiêu góc tạo thành từ tất cả các tia trên? 
----------HẾT---------- 
ĐỀ CHÍNH THỨC 
 UBND HUYỆN  ĐỀ THI OLYMPIC TOÁN 
 PHONG GD&DT. Năm học: 2014 – 2015 
 MÔN: TOÁN LỚP 6 
Thời gian: 150 phút (Không kể thời gian giao đề) 
CÂU ĐÁP ÁN ĐIỂM 
Câu 1: 
(6,0 
điểm) 
a) Cho 
7
2013
7
_
2012
7
2015
7
2014
7
2015
4
2014
4
2013
4
2012
4
4


A = 
7
4
 và 
22
2...221
2015
20132


B = 
2
1
. Suy ra A > B 
b) Tìm x biết (x + 1) + (x + 2) + (x + 3) + ... + (x + 100) = 5750. 
 100x + 101.50 = 5750 
 x = 7 
c) Cho B = 3 + 32 + 33 + 34 + 3100 
 B = (3 + 32 + 33+ 34) ++ (397+398+399+3100) 
 = 3 (1 + 3 + 32+33)+.+ 397(1+3+32+33) 
 = 40. (3 + 35 +39 ++397 ) : 40 
d) S = 
92 2
3
...
2
3
2
3
3  
 = 






82 2
3
...
2
3
2
3
3
2
1
3 
Mà 
82 2
3
...
2
3
2
3
3  = S - 
92
3
Suy ra S = 
2
1
3 ( S - 
92
3
) hay 
9
3
2 6
2
S S   
Suy ra S = 6 - 
92
3
= 6 - 
512
3
= 
512
3069
Câu 2: 
(4,5 
điểm) 
a) Tìm số x có chữ số tận cùng bằng 2, biết rằng x, 2x, 3x đều là 
các số có 3 chữ số và 9 chữ số của 3 số đó đều khác nhau và  0. 
Tìm được 3x = 576 => x = 192, 2x = 384 (đúng) 
b) Tìm số tự nhiên nhỏ nhất, biết rằng số đó khi chia cho 3, cho 4, cho 5, 
cho 6 đều dư là 2, còn chia cho 7 thì dư 3. 
Gọi số tự nhiên đó là a, ta có a = BC(3; 4; 5; 6) + 2. Mà BC( 3; 4; 5; 6) = 60; 
120; 180; 240;  
Nên a nhận các giá trị 62; 122; 182; 242 . 
 Mặt khác a là số nhỏ nhất chia cho 7 thì dư 3 nên a = 1 
ĐÁP ÁN ĐỀ CHÍNH 
THỨC 
c) Tìm hai số tự nhiên biết tổng ƯCLL và BCNN của chúng bằng 23 
Gọi hai số tự nhiên đó là a ; b ( a ; b N) Gọi d = ƯCNL(a ; b) ta có : a = 
a’.d ; b = b’.d (a’ ; b’) =1 
Khi đó BCNN(a ; b) = 
.
( ; )
a b
UCLN a b
 = 
2'. '.a b d
d
= a’.b’.d 
Theo bài ra ta có : ƯCLN(a ; b) + BCNN (a ; b) = 23 nên d + a’.b’.d = 23 = 
d (1 + a’.b’) = 23 
Nên d = 1; 1 + a’b’ =23 suy ra a’b’ = 22 mà (a’ ; b’) = 1 nên a’ = 1 ; b’ = 22 
hoặc a’ = 11; b’ = 2 và ngược lại. Từ đó HS tìm được a và b. 
Câu 3: 
(4,5 
điểm) 
a) Tìm a, b, c biết: a – b = 2013 ; b – c = –2014 ; c + a = 2015 
Tìm được a = 1007; b = –996; c = 1018 
b) Hai số tự nhiên m và n biết : BCNN(m,n)=180; ƯCLN(m,n) = 12 
Ta có: m.n = 180.12 = 2160 
Giả sử m  n. Vì ƯCLN(m,n)= 12 nên m=12p, n=12q với (p,q)=1 và pq 
Suy ra : 12p.12q = 2160 
 p.q = 15. Ta có bảng sau: 
p q m n 
1 15 12 180 
3 5 36 60 
c) Tìm số nguyên dương n để P = 
2
1
n
n
 

 là số nguyên. 
Tìm được n = 2. 
d) So sánh 23333 và 32222 
 so sánh đúng (–2)3333 < (–3)222 
Câu 4: 
(5,0 
điểm) 
- Vẽ hình đúng câu a, b được 0,5 điểm ( hs không vẽ được hình 
không tính điểm bài làm) 
 a) 
Vì 
1 1
;
2 2
xOy zOt yOz xOy     
Mà 
060zOt  nên 
0 0 0 01 1 160 30 ; 30 15
2 2 2
xOy yOz xOy         
Tính được 
0 0 0 030 15 60 105xOt xOy zOy zOt         
b) 
 Ta có 2 trường hợp: 
TH1: Tia Om nằm giữa tia Oz và tia Ot 
Tính được 
0 0 060 20 40zOm zOt tOm       
TH2: Tia Ot nằm giữa 2 tia Om và Oz 
Tính được 
0 0 020 60 80zOm mOt tOz       
c) 
Số góc tạo thành từ 2015 tia phân biệt chung gốc là : 2029105góc 
 Chú ý: 
1) Nếu học sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì cho đủ số 
điểm từng phần như hướng dẫn quy định. 
2) Bài hình không vẽ hình thì không chấm điểm. 
x 
O 
y 
z 
t 
020
m 
x 
O 
y 
z 
t 
020
m