Đề thi kiểm tra học kì 1 môn: Toán (nâng cao)

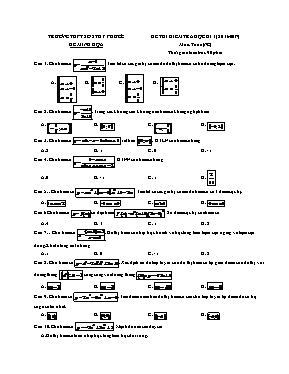
TRƯỜNG THPT SỐ 2 TUY PHƯỚC
ĐỀ MINH HỌA
ĐỀ THI KIỄM TRA HỌC KÌ 1(2016-2017) 
Môn: Toán(NC) 
Thời gian làm bài: 90 phút
Câu 1: Cho hàm số . Tìm tất cả các giá trị của m để đồ thị hàm số có ba đường tiệm cận. 
	A. 	B. 	C. 	D. 
Câu 2: Cho hàm số . Trong các khoảng sau khoảng nào hàm số không nghịch biến 
	A. 	B. 	C. 	D. 
Câu 3: Cho hàm số xét trên . GTLN của hàm số bằng
	A. 2	B. 1	C. 0	D. -1
Câu 4: Cho hàm số . GTNN của hàm số bằng: 
	A. 0	B. -1	C. 1	D. 
Câu 5: : Cho hàm số . Tìm tất cả các giá trị của m để hàm số có 3 điểm cực trị. 
	A. 	B. 	C. 	D. 
Câu 6 Cho hàm số có đạo hàm . Số điểm cực trị của hàm số
	A. 4	B. 3	C. 1	D. 2
Câu 7: : Cho hàm số . Đồ thị hàm số nhận trục hoành và trục tung làm tiệm cận ngang và tiệm cận đứng. Khi đó tổng m+n bằng:
	A. 1	B. 0	C. -1	D. 2
Câu 8: Cho hàm số . Xác định m để tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị với đường thẳng song song với đường thẳng 
	A. 	B. 	C. 	D. 
Câu 9: Cho hàm số . Tìm điểm nằm trên đồ thị hàm số sao cho tiếp tuyến tại điểm đó có hệ số góc nhỏ nhất. 
	A. 	B. 	C. 	D. 
Câu 10: Cho hàm số . Mệnh đề nào sau đây sai 
	A. Đồ thị hàm số luôn nhận trục tung làm trục đối xứng. 
	B. Đồ thị hàm số luôn có 3 điểm cực trị. 
	C. Đồ thị hàm số không cắt trục hoành. 
	D. Đồ thị hàm số luôn đi qua điểm 
Câu 11: Với giá trị nào của tham số m thì hàm số đồng biến trên khoảng 
A. B. C. D. 
Câu 12: : Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a. Thể tích của (H) bằng:
A. 	B. 	C. 	D. 
Câu 13: : Cho hình hộp chữ nhật có . Thể tích hình hộp chữ nhật bằng
A. B. C. D. 
Câu 14: Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a và chiều cao của hình chóp là . Tính theo a thể tích khối chóp S.ABCD.
A. B. C. D. 
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành với AB=a, AD=2a, , SA vuông góc với đáy, góc giữa SC và đáy bằng . Thể tích khối chóp S.ABCD là V. Tỷ số là
A. 	B. 	C. 	D. 
Câu 16 Cho hình chóp đều S.ABC có cạnh đáy bằng . Góc giữa cạnh bên và mặt đáy bằng 600. Tính theo a thể tích khối chóp S.ABC. 
A. B. C. D. 
Câu 17: Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a và chiều cao của hình chóp là . Tính theo a thể tích khối chóp S.ABCD.
A. B. C. D. 
Câu 18 Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B. AB = . SA vuông góc với đáy và SA = a. Tính khoảng cách từ điểm A đến mp(SBC) 
A. B. C. D. 
Câu 19: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc H của S lên mặt (ABCD) là trung điểm của đoạn AB. Gọi K là trung điểm của AD. Tính khoảng cách giữa hai đường thẳng SD và HK theo a
A. 	B. 	C. 	D. 
Câu 20: Tìm giới hạn sau A=limx→0e3xx-e5xx
A.-2	B.1	C.2	D.-1
Câu 21:Tìm tập xác định của hàm số sau:√x2-5x+6+ln4x2-4
A.D=(-∞;2)∪3;+∞)	B. =(-∞;-2)∪3;+∞)	C. =(-∞;4)∪5;+∞)	D. =(-∞;2)∪-3;+∞)
Câu22: Tìm m để hàm số sau xác định: log2(2x+3x+2m-1)
A. D=(-∞;2)	B. =(-∞;-2)	C. (1;+∞)	D. (-1;+∞)
Câu 23: Tính đạo hàm của hàm số sau 51+2x3
A.6X255(1+2X3)4	B..6X255(1-2X3)4	C. .6X255(1+X3)4	D.X255(1+X3)4
Câu 24: Cho hàm số f(x)=2x-52ln(1+x2). Chon khẳng định đúng:
Hàm số không có cực trị 
Hàm số nghịch biến trên khoảng (12;2)
Hàm số đồng biến trên khoảng(-∞;12) và (2;+∞)
Cả a và b đều đúng
Câu 25: Giải phương trình sau:(122)x2-3x+2=642x-132.
A.x=3,x=8	b.x=3,x=-8	c.x=-3,x=-8	D.x=-3,x=8
Câu 26: Biểu diễn các số đây theo a=ln2; b=ln5:A= ln12+ln23++ln9899+ln99100.
A.-2a+2b	B.-2a-2b	C.-2a+3b	D.-2a-3b
Câu 27: Sử dụng công thức L(dB)=10logIIO. Hãy tính độ lớn L biết ở tiếng máy bay phản lực IIo=2.3×1012
A.-125dB	B.125dB	C.126dB	D.-126Db
Câu 28: Một người gửi 15 triệu đồng vào ngân hang theo thể thức lãi kép kì hạn một quý với lãi suất 1.65%một quý Hỏi sau bao lâu người đó có được ít nhất 20 triệu đồng( cả vốn lẫn lãi) từ số vốn ban đầu?( Giả sử lãi suất không thay đổi)
A.4 năm ,3 quý	B. 4 năm,1 quý	C. 4 năm, 2 quý	D.3 năm , 2 quý
Câu 29 Đơn giản biểu thức sau:4(a3b2)43a12b6
A.a+b	B.a.b	C.a-b	D.2a+2b
Câu 30 Tìm tất cả các giá trị của x,y thỏa mãn:x4+y2≤1x5+y3≥1
A.(x,y)=(0,1) và (1,0)	B.(0,1) và (1,1)	C.(1,1) và (-1,0)	D.(0,-1) và(-1,0)
------------------------------------------------------------HẾT-------------------------------------------------------------------------
TRƯỜNG THPT SỐ 2 TUY PHƯỚC
ĐỀ CHÍNH THỨC
ĐỀ THI KIỄM TRA HỌC KÌ 1(2016-2017) 
Môn: Toán(NC) 
Thời gian làm bài: 90 phút
	ĐÁP ÁN BIỂU ĐIỂM:
ĐÁP ÁN CẬP NHẬP TẠI WEB THPT SỐ 2 TUY PHƯỚC VIOLET. CÓ LỜI GIẢI CHI TIẾT( NGÀY 10.12.2016) VÀI CÂU MINH HỌA BẠN ĐỌC CÓ THỂ NHẬP EMAIL BÊN DƯỚI ĐỂ ĐƯỢC SEND ĐÁP ÁN
Câu 1: Chọn A
Nhận thấy đồ thị hàm số có 3 đường tiệm cận khi hàm số đã cho có dạng bậc nhất trên bậc 2 hay (khi thì hàm số có 2 tiệm cận đứng và tiệm cận ngang)
Điều kiện để đồ thị hàm số có 3 tiệm cận là có 2 nghiệm phân biệt khác 1 tức là và hay và .
Vậy thỏa mãn yêu cầu bài ra. Chọn A.
Câu 2: Chọn D 
nên hàm số luôn nghịch biến trên và . Vậy hàm số không nghịch biến trên . Chọn D 
Câu 3: Chọn B 
Với (các bạn tự xem lạ hệthống kiến thức về phần đồng biến nghịch biến của các hàm lượng giác)
Đặt 
Theo bài ra ta có 
Vẽ nhanh bảng biến thiên của hàm số với ta thấy giá trị lớn nhất của hàm số là . Chọn B.
Câu : Chọn B 
Vì nên . Chọn B.
Câu : Chọn D
 ta có 
Vì hàm số liên tục và xác định trên đoạn nên ta có 
Vậy . Chọn D.
Câu : Chọn A 
Gọi cạnh đáy của lăng trụ là a, chiều cao lăng trụ là h. 
Theo bài ra ta có 
Diện tích toàn phần của lăng trụ là 
Áp dụng bất đẳng thức AM - GM ta có
Dấu bằng xảy ra khi hay . Chọn A
Nhận xét: Bài trên các em phải vận dụng linh hoạt bất đẳng thức AM-GM thì mới tìm được giá trị nhỏ nhất của diện tích xung quanh của hình lăng trụ sau đó dựa vào điều kiện xảy ra dấu bằng để tìm cạnh đáy của hình lăng trụ. 
Câu : Chọn D
Ta có 
Hàm số c 3 điểm cực trị khi và chỉ khi phương trình có 3 nghiệm phân biệt. Vậy (I) có 2 nghiệm phân biệt khác 0 hay . Chọn D.
Câu : Chọn D
Lập bảng xét dấu của các em sẽ thấy được các điểm cực trị là , khi đi qua điểm 0 thì không đổi dấu
Nhận xét
Các em chú ý tới thì n chẵn không đổi dấu qua , còn n lẻ thì đổi dấu 
Câu : Chọn B
Đồ thị hàm số bậc nhất trên bậc nhất có đường tiệm cận đứng và tiệm cận ngang .
Đồ thị hàm số có tiệm cận đứng và tiệm cận ngang lần lượt là trục tung và trục hoành hay . Chọn B 
Câu : Chọn C 
Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm 
Điều kiện để đường thẳng trên song song với đường thẳng là nên Chọn C.
Câu 11. Chọn C
Gọi x0 là hoành độ của tiếp điểm theo bài ra ta có 
Dấu bằng xảy ra khi 
Vậy điểm cần tìm là nên chọn C 
Câu : Chọn C 
A. Đúng vì đồ thị hàm trùng phương luôn nhận trục tung là trục đối xứng 
B. Đúng vì phương trình luôn có 3 nghiệm phân biệt nên đồ thị hàm số có 3 điểm cực trị.
C. Sai
D. Đúng
Câu : Chọn B 
Ta có v
Để hàm số nghịch biến trên thì
 nên chọn B.