Đề thi khảo sát chất lượng giữa kỳ I môn Toán Lớp 12 - Mã đề 1201 - Trường THPT Nho Quan C

TRƯỜNG THPT NHO QUAN C ĐỀ THI KHẢO SÁT CHẤT LƯỢNG GIỮA KỲ I
 TỔ TOÁN TIN NĂM HỌC 2016-2017
MÃ ĐỀ 1201 ( Thời gian 90 phút)
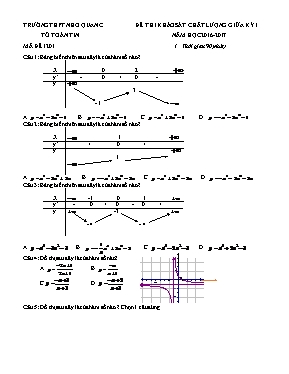
Câu 1: Bảng biến thiên sau đây là của hàm số nào? 
 X 0 2 
 y’ - 0 + 0 - 
 y 
 3
 - 1 
A. B. C. D. 
Câu 2: Bảng biến thiên sau đây là của hàm số nào? 
 X 1 
 y’ + 0 +
 y 
 1 
A. B. C. D. 
Câu 3: Bảng biến thiên sau đây là của hàm số nào? 
 X -1 0 1 
 y’ - 0 + 0 - 0 +
 y -3 
 - 4 - 4 
A. B. C. D. 
Câu 4: 
Đồ thị sau đây là của hàm số nào?
A. 	B. 
C. 	D. 
Câu 5: Đồ thị sau đây là của hàm số nào ? Chọn 1 câu đúng.
A. B. C. D. 
Câu 6: 
Đồ thị sau đây là của hàm số nào?
A. 
B. 
C. 
D. 
Câu 7: Đồ thị sau đây là của hàm số. Với giá trị nào của m thì phương trình 
có ba nghiệm phân biệt. ? Chọn 1 câu đúng.
A. m = -3 B. m = - 4 C. m = 0 D. m = 4 
Câu 8. Hàm số y = nghịch biến trên tập nào sau đây?
a) R b) ( -; -1) ( 3; +) c) ( 3; +) d) (-1;3)
Câu 9. Hàm số y = nghịch biến trên tập nào sau đây?
A. R B. ( -;-1) và (-1;+ ) C. ( -;1) và (1;+ ) D. R \ {-1; 1}
Câu 10. Hàm số y = . Với giá trị nào của m thì hàm số trên luôn đồng biến trên từng khoảng xác định của nó.
A. m = 2 B.m = -2 C. -2 2
Câu 11: Tìm m để hàm số đồng biến trên khoảng .
 A. -13 B. [13; + ) C. (13; + ) D. (- ; 13).
Câu 12: Tìm giá trị của m để hàm số nghịch biến trên R.
 A. ( -1; 0) B. [-1; 0] C. ( - ; -1) (0; +) D. ( - ; -1] [ 0; +) 
Câu 13: Hàm số có bao nhiêu điểm cực trị
A. Có 3	 B. Có 2	 C. Có 1	 D. Không có
Câu 14 : Với giá trị nào của m thì hàm số đạt cực tiểu tại điểm 
A. 	B. 	 C. 	 D. 
Câu 15. Điểm cực đại của hàm số y = là:
 A) x =0 B) x = 2 C) (0; 2) D) ( 2; 7)
Câu 16. Hàm số y = đạt cực tiểu tại x = 1 khi
A) m = 0 B) m = -1 C) m = - 2 D) m = -3
Câu 17. Hàm số có cực tiểu và cực đại khi: 
A) m > 0 B) m < 0 C) m 0 D) m 
Câu 18. Giá trị lớn nhất, nhỏ nhất của hàm số: trên đoạn [-4; 4] lần lượt là:
a) 4; -6 b) 4; -18 c) 10; -2 d) 14; -114
Câu 19: Giá trị nhỏ nhất của hàm số trên đoạn [ 2 ; 4 ] là :
A. 0 B. – 5 C. -10 D. – 3
Câu 20: Giá trị lớn nhất của hàm số trên đoạn [ 2 ; 3 ] là khi m nhận giá trị
A. 0 B. 1 C. -5 D. – 2
Câu 21. Giá trị nhỏ nhất của hàm số: trên nửa đoạn [0; +) lần lượt là:
A. -2 B. 4	C. -4 D. -14
Câu 22. Giá trị lớn nhất, nhỏ nhất của hàm số: lần lượt là:
A. 4; -4 B. 4; 4 C. 4; -4 D. 4; 2
Câu 23: Cho hàm số . Chọn đáp án sai ?
A. Hàm số luôn có cực đại và cực tiểu;	 B. Hàm số đạt cực tiểu tại x = 2;
C. Hàm số đồng biến trên khoảng ;	D. f’’(1)=0
Câu 24. Hàm số nào có đồ thị nhận đường thẳng x = -2 làm đường tiệm cận:
 A.  B.  C.  D.  
. Câu 25. Cho hàm số . Trong các câu sau, câu nào sai.
A. B. C. TCĐ x = 2	 D. TCN y= - 2 
Câu 26. Phương trình các đường tiệm cận của đồ thị hàm số  là:
 A. y= 1 và x = 3 B. y = x+2 và x = 1 C. y = 3 và x = 1 D. y = -3 và x = 1
Câu 27: Phương trình tiếp tuyến với đồ thị hàm số có hệ số góc k = 3 là:
A. 	B. 	C. 	D. Khác
Câu 28: Giá trị m để phương trình có 4 nghiệm phân biệt
	A. 	B. 	C. 	D 
Câu 29: Đồ thị hàm số có phương trình tiếp tuyến tại điểm có hoành độ x = 0 là
	A. 	B. 	C. 	D. 
Câu 30. Tìm m để đường thẳng (d): y = mx – 2m + 4 cắt đồ thị (C) của hàm số tại ba điểm phân biệt 
	A. B. m > 0 C. m < 0	 D. 
Câu 31: Đường thẳng y = m cắt đồ thị hàm số tại 3 điểm phân biệt khi :
A. 	B.m < - 2	C. 	D. -2< m < 4
Câu 32.Giá trị m để hàm số đạt cực đại tại là:
A. 	B. 	C. 	D. Không có m nào 
Câu 33.  Một người mua xe air blade 50 triệu, trả góp theo tháng trong vòng 48 tháng, lãi là 1,15%/tháng.Hỏi hàng tháng phải trả bao nhiêu?(đơn vị việt nam đồng)
A. 1361310 đồng B. 1361312,807 đồng C. 1361311 đồng D. 1361312 đồng
O
A
C
B
1,4
1,8
Câu 34. Mét mµn ¶nh ch÷ nhËt cao 1,4m ®­îc ®Æt ë ®é cao 1,8m so víi tÇm m¾t (tÝnh ®Çu mÐp d­íi cña mµn ¶nh). §Ó nh×n râ nhÊt ph¶i x¸c ®Þnh vÞ trÝ ®øng sao cho gãc nh×n lín nhÊt. H·y x¸c ®Þnh vÞ trÝ ®ã là?
2 mét B. 3 mét C 2,4 mét D. 3,4 mét
Câu 35: Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a là:
A. 	B. 	C. 	D. 
Câu 36: Cho hình lăng trụ ngũ giác ABCDE.A’B’C’D’E’. Gọi A’’, B’’, C’’,D”, E’’ lần lượt là trung điểm của các cạnh AA’, BB’, CC’, DD’, EE’. Tỉ số thể tích giữa khối lăng trụ ABCDE.A’’B’’C’’D’’E’’ và khối lăng trụ ABCDE.A’B’C’D’E’ bằng:
A. 	B. 	C. 	D. 
Câu 37: Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A’ trên cạnh SA sao cho . Mặt phẳng qua A’ và song song với đáy của hình chóp cắt các cạnh SB, SC, SD lần lượt tại B’, C’, D’. Khi đó thể tích khối chóp S.A’B’C’D’ bằng:
A. 	B. 	C. 	D. 
Câu 38: Người ta muốn xây một bồn chứa nước dạng khối hộp chữ nhật trong một phòng tắm. Biết chiều dài, chiều rộng, chiều cao của khối hộp đó lần lượt là 5m, 1m, 2m ( hình vẽ bên). Biết mỗi viên gạch có chiều dài 20cm, chiều rộng 10cm, chiều cao 5cm. Hỏi người ta sử dụng ít nhất bao nhiêu viên gạch để xây bồn đó và thể tích thực của bồn chứa bao nhiêu lít nước? (Giả sử lượng xi măng và cát không đáng kể )
A. B. 	 C. 	 D. 
 Câu 39: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M và N theo thứ tự là trung điểm của SA và SB. Tỉ số thể tích  là: 
A. 	B. 	C. 	D. 
Câu 40: Cho lăng trụ có đáy là tam giác đều cạnh a , Hình chiếu vuông góc của điểm lên mặt phẳng trùng với trọng tâm tam giác . Biết khoảng cách giữa hai đường thẳng và bằng . Khi đó thể tích của khối lăng trụ là
A. 	B. 	C. 	D. 
Câu 41: Một lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác đều ABC cạnh . Cạnh bên bằng b và hợp với mặt đáy góc . Thể tích hình chóp .BCC’B’ bằng bao nhiêu ?
A. 	B. 	C. 	D. 
Câu 42: Cho ABCD.A’B’C’D’ là hình lập phương có cạnh . Thể tích của tứ diện ACD’B’ bằng bao nhiêu ?
A. 	B. 	C. 	D. 
Câu43: Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; biết , . Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 600. Gọi I là trung điểm của AD, biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Thể tích khối chóp S.ABCD là:
A. 	B. 	C. 	D. 
Câu44: Cho một tứ diện đều có chiều cao h. Ở ba góc của tứ diện người ta cắt đi các tứ diện đều bằng nhau có chiều cao x để khối đa diện còn lại có thể tích bằng một nửa thể tích tứ diện đều ban đầu ( hình bên dưới ). Giá trị của x là bao nhiêu?
A. 	B. 	C. 	D. 
Câu45: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, cạnh SA vuông góc với mặt đáy , biết AB=2a, SB=3a. Thể tích khối chóp S.ABC là V. Tỷ số có giá trị là.
A. 	B. 	C. 	D. 
Câu46: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I và có cạnh bằng a, góc . Gọi H là trung điểm của IB và SH vuông góc với (ABCD). Góc giữa SC và (ABCD) bằng . Tính thể tích khối chóp S.AHCD.
A. 	B. 	C. 	D. 
Câu47: Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại A, AC=a, . Đường chéo BC’ của mặt bên (BCC’B’) tạo với mặt phẳng (AA’C’C) một góc . Tính thể tích của khối lăng trụ theo a
A. 	B. 	C. 	D. 
Câu48: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành với AB=a, AD=2a, , SA vuông góc với đáy, góc giữa SC và đáy bằng . Thể tích khối chóp S.ABCD là V. Tỷ số là
A. 	B. 	C. 	D. 
Câu49: Cho hình chóp S.ABC có đáy là tam giác cân tại A, AB=AC=a, . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABC
A. 	B. 	C. 	D. 
Câu 50: Cho hình chóp SABC có ; SBC là tam giác đều cạnh a và (SAB) (ABC). Tính thể tích khối chóp SABC.
A. 	B. 	C. 	D. 
HỌ TÊN THÍ SINH:............................................................................ SBD:...................................................
CHỮ KÝ GIÁM THỊ..............................................................................................................................................