Đề thi học sinh giỏi thực hành năm học 2009 - 2010 môn: giải Toán trên máy casio lớp 9

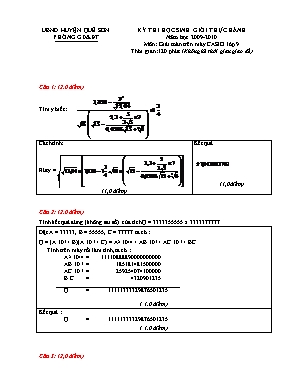
UBND HUYỆN QUẾ SƠN
PHÒNG GD&ĐT
KỲ THI HỌC SINH GIỎI THỰC HÀNH
Năm học 2009-2010
Môn: Giải toán trên máy CASIO lớp 9
Thời gian: 120 phút (Không kể thời gian giao đề)
Câu 1: (2.0 điểm)
Tìm y biết: 
Cách tính:
Rút y =
(1,0 điểm)
Kết quả
(1,0 điểm)
Câu 2: (2.0 điểm)
Tính kết quả đúng (không sai số) của tích Q = 3333355555 x 3333377777
Đặt A = 33333, B = 55555, C = 77777 ta có : 
Q = (A.105 + B)(A.105 + C) = A2.1010 + AB.105 + AC.105 + BC
	Tính trên máy rồi làm tính, ta có : 
A2.10 10 	= 	11110888890000000000
AB.105 	=	185181481500000
AC.105	= 	259254074100000
B.C 	=	4320901235 
Q	= 11111333329876501235
( 1.0 điểm)
Kết quả :
Q	= 11111333329876501235
( 1.0 điểm)
Câu 3: (2,0 điểm)
Giải phương trình : 
Cách tính:
- Tính vế phải.
- Thực hiện: Chia 20 - Lấy nghịch đảo - Trừ 2 - Lấy nghịch đảo - Trừ 3 - Lấy nghịch đảo - Trừ 4 - Lấy nghịch đảo
(1.0 điểm)
Kết quả:
x = -0,2333629 
(1.0 điểm) 
Bài 4: (2.0 điểm) 
Tìm các ước nguyên tố của 
Cách tính:
Tìm ƯCLN(1751,1957,2369) = 103.
 A = 1033(173 + 193 + 233) = 1033 . 23939.
 Chia 23939 cho các số nguyên tố 2. 3, 5, ., 37 ta được 23939 = 37 . 647
 Do 647 < 372 nên 647 là số nguyên tố .
(1,5 điểm)
Kết quả:
 37; 103; 647
(0,5 điểm)
Câu 5: (3.0 điểm):
Tìm số tự nhiên lớn nhất có 10 chữ số .Biết số đó chia 19 dư 12 ,chia 31 dư 13
Cách tính:
- Tìm số nhỏ nhất thoả điều kiện chia 19 dư 12 ,chia 31 dư 13: Bội của 31 + 13 - 12 chia hết cho 19. Hay Bội của 31 + 1 chia hết cho 19.
- Dùng máy tính (Cho biến A chạy từ 1 xét 31A + 1 chia 19) tìm được số A là 11 => 354
- Các số khác thoả điều kiện này là B(BCNN(31,19))+354.
- Theo điều kiện số tự nhiên lớn nhất có 10 chữ số
K. 589 + 354 < 9999999999
K £ 16977928,09. Lấy K = 16977928 
(Mỗi bước cho 0,5 điểm)
Kết quả:
 9999999946
(0,5 điểm)
Câu 6: (2.0 điểm)
Tìm xy để số 1234xy345 chia hết cho 12345 
Cách tính: 
- Có 0 £ xy £ 99. 
- Gọi thương của 1234xy345 cho 12345 là k ta có:
123400345123 £ 12345.k £ 123499345
 9995.969 £ k £ 10003.99
- Xét 9996 £ k £ 10003 có k = 10001 cho kết quả 123462345 (Thoả)
(Mỗi y cho 0,5 điểm)
Kết quả:
xy = 62
( 123462345)
(0,5 điểm)
Câu 7:(4.0 điểm) 
Cho đa thức : Q(x) = x5 + ax4 – bx3 + cx2 + dx – 2010
Biết rằng khi x nhận các giá trị lần lượt 1, 2, 3, 4 thì Q(x) có các giá trị tương ứng là 9, 21, 33, 45.
a. Xác định các hệ số a, b, c, d và tính giá trị của đa thức.
b. Tại các giá trị của x = 1,15 ; 1,25 ; 1,35 ; 1,45.
Cách tính:
- Thay x = 1, 2, 3, 4 ta được hệ : 
- Đưa về hệ bậc nhất 3 ẩn: (Lấy hai vế của phương trình (1) lần lượt nhân với 2, 3, 4 rồi trừ lần lượt vế đối vế với phương trình (2), phương trình (3), phương trình (4), ta được hệ phương trình bậc nhất 3 ẩn) :
Và dùng chức năng của máy để giải hệ bậc nhất ba ẩn
- Ta có P(x)=x5 – 93,5x4 + 870x3 -2972,5x2+ 4211x – 2007
- Dùng chức năng CALC để nhập và tính giá trị của biểu thức
(2.0 điểm)
Kết quả:
a =-93,5
b = -870
c = -2972,5
d = 4211
Q(1,15) = 63,15927281
Q(1,25) = 83,21777344	
Q(1,35) = 91,91819906	
Q(1,45) = 91,66489969
(2.0 điểm)
Câu 8: (2.0 điểm)
 Cho dãy số sắp với thứ tự U1 = 2; U2 = 20 và từ U3 trở đi được tính theo công thức (với ).
Viết quy trình bấm phím liên tục để tính giá trị Un với U1 = 2; U2 = 20.
Sử dụng quy trình trên để tính U23; U24; U25
Gán:
A = 2
B = 20
D = 2 (Biến đếm)
D=D+1:A=2*B+A:D=D+1:B=2*A+B
Ấn liên tiếp = xem giá trị D để biết số hạng thứ và xem A, B để biết giá trị của số hạng.
(1,0 điểm)
Kết quả:
U23 = 1941675090
U24 = 4687618336
(0,5 điểm)
U25 = 11316911762
(0,5 điểm)
Câu 9: (3.0 điểm)
	Tam giác ABC có số đo ba cạnh lần lượt là 6 (cm), 8 (cm), 10 (cm). G là trọng tâm của tam giác. Tính tổng GA + GB + GC.
Cách tính:
- Chứng tỏ được tam giác ABC vuông.
- Trung tuyến ứng với cạnh 10 (cm) bằng: 5 (cm)
- Trung tuyến ứng với cạnh 6 (cm): 
- Trung tuyến ứng với cạnh 8 (cm): 
- GA + GB + GC = (Tổng ba trung tuyến).
(Mỗi ‎ bước cho 0,5 điểm)
Hình vẽ:
Kết quả:
 13,83673753 (cm)
(0,50 điểm)
Câu 10: (4.0 điểm)
Cho tam giác ABC vuông tại A. Biết , góc C = 40025’. Từ A vẽ đường phân giác AD và trung tuyến AM (D và M thuộc BC)
a. Tính độ dài của các đoạn thẳng AM, BD.
b. Tính diện tích các tam giác ADM. 
c. Tính độ dài phân giác AD.
Cách tính:
- Tính BC:
 . .
- Tính BD:
.
Gọi x, y lần lượt là độ dài BD, DC có hệ:
- Tính SADM: 
SABC = = 
- Tính AD:
Hạ đường cao AH của tam giác ABC.
Có 
ÐHAD = 450 - 42025’ = 2035’
(Mỗi bước cho 0,5 điểm)
A
B
C
M
D
Kết quả:
AM = 4,051723391
BD = 3.726915668 (cm)
SADM = 0,649613583
AD = 4,012811598
(Mỗi kết quả cho 0, 50 điểm)
Câu11: (4.0 điểm)
	Cho đường tròn (O) có bán kính 2(cm). O’O = 4cm. O’A là tiếp tuyến của (O). Đường tròn tâm O’ bán kính O’A cắt (O) tại B. Tìm diện tích phần chung S của hai hình tròn (Phần tô đậm).
Cách giải:
- Chứng tỏ DAMO đều (1.0 điểm)
 DAO’O vuông tại A.
 Gọi M là giao điểm của OO’ với (O) ta có: 
 MO’=MO (=2cm).
 => AM là trung tuyến => AM = OO’/2 = 2(cm)
 => DAMO đều 
- Suy ra các số liệu cần thiết (0,75 điểm)
=> ÐAOM = 600 ; ÐAO’M = 300. O’A = 
- Xây dựng công thức tính diện tích (1.0 điểm)
 S = Squạt o’ AB + Squạt o AB - SAOBO’ 
- Tính toán diện tích các hình (0,75 điểm)
 Squạt o’ AB = ; Squạt o AB = 
 SAOBO’ = 2.SAOO’ = 
 S = 2p + p - 
Kết quả:
 S = 3.543772282 (cm2)
(0,50 điểm)
Một số lưu ý khi chấm:
Học sinh được phép sử dụng các loại máy khác nhau, sử dụng các phương pháp khác nhau để giải nên khi chấm giám khảo cần có sự linh hoạt phân điểm cho phù hợp.
Phương pháp giải chỉ yêu cầu trình bày ngắn gọn, thể hiện được cách tính, không yêu cầu chứng minh chặc chẽ, biến đổi chi tiết (HDC nêu chi tiết để tiện theo dõi).
Khi mắc các lỗi sau thì trừ một nửa số điểm của phần đó: Không đạt độ chính xác cao nhất, Không ghi đơn vị