Đề thi học kỳ I môn Toán Lớp 12 (Chương trình chuẩn) - Năm học 2016-2017 - Nguyễn Văn Huy

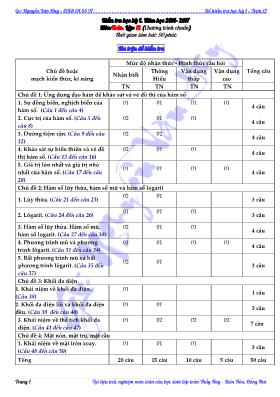
Gv: Nguyễn Văn Huy – 0968 64 65 97 Đề kiểm tra học kỳ 1 – Toán 12 
Trang 1 Tại liệu trắc nghiệm môn toán của học sinh lớp toán Thầy Huy – Biên Hòa, Đồng Nai 
 Kiểm tra học kỳ I. Năm học 2016- 2017 
Môn:Toán. Lớp: 12 (Chương trình chuẩn) 
Thời gian làm bài: 90 phút; 
Ma trận đề kiểm tra 
Chủ đề hoặc 
mạch kiến thức, kĩ năng 
Mức độ nhận thức - Hình thức câu hỏi 
Tổng câu 
Nhận biết 
Thông 
Hiểu 
Vận dụng 
thấp 
Vận dụng 
cao 
TN TN TN TN 
Chủ đề 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 
1. Sự đồng biến, nghịch biến của 
hàm số. (Câu 1 đến câu 4) 
01 
01 
01 
01 
4 câu 
2. Cực trị của hàm số. (Câu 5 đến 
câu 8) 
02 
01 
01 
 4 câu 
3. Đường tiệm cận. (Câu 9 đến câu 
12) 
02 
02 
 4 câu 
4. Khảo sát sự biến thiên và vẽ đồ 
thị hàm số. (Câu 13 đến câu 16) 
02 
01 
01 
 4 câu 
5. Giá trị lớn nhất và giá trị nhỏ 
nhất của hàm số. (Câu 17 đến câu 
20) 
01 
01 
01 
01 
4 câu 
Chủ đề 2: Hàm số lũy thừa, hàm số mũ và hàm số logarit 
1. Lũy thừa. (Câu 21 đến câu 23) 
02 
01 
 3 câu 
2. Lôgarit. (Câu 24 đến câu 26) 
01 
01 
01 
 3 câu 
3. Hàm số lũy thừa. Hàm số mũ, 
hàm số logarit. (Câu 27 đến câu 30) 
02 
01 
01 
 4 câu 
4. Phương trình mũ và phương 
trình lôgarit. (Câu 31 đến câu 34) 
01 
01 
01 
01 
4 câu 
5. Bất phương trình mũ và bất 
phương trình lôgarit. (Câu 35 đến 
câu 37) 
02 
01 
 3 câu 
Chủ đề 3: Khối đa diện 
1. Khái niệm về khối đa diện.. 
(Câu 38) 
01 
 1 câu 
2. Khối đa diện lồi và khối đa diện 
đều. (Câu 39 đến câu 40) 
01 
01 
 2 câu 
3. Khái niệm về thể tích khối đa 
diện. (Câu 41 đến câu 47) 
01 
02 
02 
02 
7 câu 
Chủ đề 4: Mặt nón, mặt trụ, mặt cầu 
1. Khái niệm về mặt tròn xoay. 
(Câu 48 đến câu 50) 
01 
01 
01 
 3 câu 
Tổng 20 câu 15 câu 10 câu 5 câu 50 câu 
Gv: Nguyễn Văn Huy – 0968 64 65 97 Đề kiểm tra học kỳ 1 – Toán 12 
Trang 2 Tại liệu trắc nghiệm môn toán của học sinh lớp toán Thầy Huy – Biên Hòa, Đồng Nai 
Câu 1. Hàm số   4 2y x x 4 đồng biến trên: 
A.  0; B.  ; 0 C.  1;1 D.  . 
Câu 2. Hàm số   2y 25 x 
A. Đồng biến trên khoảng ( 5;0) và (0;5). 
B. Đồng biến trên khoảng ( 5;0) và nghịch biến trên khoảng (0;5). 
C. Nghịch biến trên khoảng ( 5;0) và đồng biến trên khoảng (0;5). 
D. Nghịch biến trên khoảng ( 6;6). 
Câu 3. Điều kiện của a, b, c để hàm số   3y ax bx c luôn nghịch biến trên R là: 
A.   ab 0, c R B.    a 0,b 0, c R 
C.   ab 0, c R D.    a 0,b 0, c R 
Câu 4. Với giá trị nào của tham số m thì hàm số 
 

x 3m 1y
x m
 nghịch biến trên (3; ) . 
A.  1 m 3
4
 B.  1 m 3
4
 C.  1 m 3
4
 D.  1m
4
Câu 5. Hàm số  2 3y 3x 2x đạt cực trị tại 
A.  CD CTx 1;x 0 B.   CD CTx 1;x 0 
C.   CD CTx 0; x 1 D.  CD CTx 0;x 1 
Câu 6. Cho hàm số   4 21y x 2x 1
4
. Hàm số có 
A. Một cực đại và hai cực tiểu B. Một cực tiểu và hai cực đại 
C. Một cực đại và không có cực tiểu D. Một cực tiểu và một cực đại 
Câu 7. Hàm số      4 2y mx m 3 x 2m 1 chỉ có cực đại mà không có cực tiểu với m: 
A. m 3 B m 0 C.   3 m 0 D.   m 0 m 3 
Câu 8. Với giá trị nào của tham số thì đồ thị hàm số có cực 
đại, cực tiểu, đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một 
tam giác có diện tích bằng 
A. B. C. D. 
Câu 9. Đồ thị hàm số nào sau đây có đường tiệm cận ngang là  y 2 
A.   1y 2
x
 B. 

2xy
x 1
 C. 


1 2xy
x 3
 D. 
2
2xy
x 2
Câu 10. Độ thì hàm số nào sau đây có đường tiệm cận đứng x 2 
A. 


2x 1y
x 2
 B. 

2
x 1y
x 4
 C. 


2x 1y
x 1
 D. 


x 1y
x 2
Câu 11. Cho hàm số 


ax by
x 1
 có tiệm cận ngang là y 4và đồ thị hàm số đi qua điểm  A 2;0
thì tích a.b bằng: 
A. 32 B. 12 C. 8 D. 4 
m 3 23 3(1 ) 1 3y x x m x m     
4 ?
2.m   1.m  1.m   1.m 
Gv: Nguyễn Văn Huy – 0968 64 65 97 Đề kiểm tra học kỳ 1 – Toán 12 
Trang 3 Tại liệu trắc nghiệm môn toán của học sinh lớp toán Thầy Huy – Biên Hòa, Đồng Nai 
Câu 12. Cho hai hàm số 

 2
2x 1y
m 8 x
 và 


5 2xy
x 4
 . Tập hợp các giá trị của tham số m để hai 
đường tiệm cận đứng của hai đồ thị hàm số trên trùng nhau là: 
A.  2;2 B.  1;2 C.  0 D.  2;3 
Câu 13. Tọa độ tâm đối xứng của đồ thị hàm số    
3
2xy 2x 3x 1
3
 là: 
A.  0; 1 B.  3; 1 C.      
11;
3
 D. 
     
12;
3
Câu 14. Phương trình tiếp tuyến của    
2x 1H : y
x 2
 tại giao điểm với trục hoành là: 
A.  y 4x 2 B. y 0 C.   4x 5y 2 0 D.   y 4x 2 
Câu 15. Hàm số nào sau đây có đồ thị như hình vẽ: 
Câu 16. Đồ thị hàm số    3 2y x ax bx c đi qua ba điểm  A 1;3 ,  B 0;7 ,   C 3; 35 thì 
phương trình của hàm số là 
A.    3 2y x x 2x 7 B.     3 2y x x 2x 7 
C.    3 2y x x 2x 7 D.   3y x 2x 7 
Câu 17. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số    y 3 x 7 x lần lượt là: 
A. 10;2 5 B. 5; 10 C. 3; 7 D. 2 5; 10 
Câu 18. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số 

2
x 1y
x 1
 trên đoạn    1;2 lần lượt là: 
A.  2;0 B. 0; 2 C. 3 50;
5
 D. 
3 5 ; 2
5
Câu 19. Với giá trị nào của m thì hàm số  y sin 3x mcos x đạt cực đại tại điểm x
3
A.  m 2 3 B. m 2 3 C.  m 6 D. m 6 
Câu 20. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích 
bằng 3m
500
3
. Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân 
công để xây hồ là 500.000 đồng/m2. Hãy xác định kích thước của hồ nước sao cho chi phí 
thuê nhân công thấp nhất. Tính chi phí đó. 
A. 74 triệu đồng B. 75 triệu đồng C. 76 triệu đồng D. 77 triệu đồng 
x
y
-1
1
O
A.    3 2y x 3x 3x 
B.   3 2y x 3x 3x 
C.     3 2y x 3x 3x 1 
D.    3 2y 2x 3x 3x 
Gv: Nguyễn Văn Huy – 0968 64 65 97 Đề kiểm tra học kỳ 1 – Toán 12 
Trang 4 Tại liệu trắc nghiệm môn toán của học sinh lớp toán Thầy Huy – Biên Hòa, Đồng Nai 
Câu 21. Biểu thức 
1
2
3
1b. .b
b
 (b dương) được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 
A. 
2
3b B. 
4
3b C. 
1
6b D. 
2
3b 
Câu 22. Cho  3 27 . Mệnh đề nào sau đây là đúng? 
A. -3 3 C.  < 3 D.   R 
Câu 23. Khẳng định nào sau đây là khẳng định nào đúng . 
A. 200 3003 2 B. 2 5 3 23 3 C. 
              
100 95
1 1
2 2
 D.  2030 7 3 
Câu 24. Cho a 0 , a 1 , x, y là 2 số dương. Tìm mệnh đề đúng: 
A.    a a alog x y log x log y B.   a a alog x.y log x log y 
C.  a a alog x.y log x. log y D.   a a alog x y log x.log y 
Câu 25. Cho log2 a . Tính log 125
4
theo a? 
A. 3 - 5a B. 2(a + 5) C. 4(1 + a) D. 6 + 7a 
Câu 26. Nếu  2 2 2log x 5 log a 4 log b (a, b > 0) thì x bằng: 
A. 5 4a b B. 4 5a b C. 5a + 4b D. 4a + 5b 
Câu 27. Cho hàm số  xy x(e ln x) . Chọn khẳng định đúng: 
A. Hàm số có đạo hàm tại x = 0. B. Hàm số xác định với mọi x dương. 
C. Hàm số không có đạo hàm tại x = 1. D. Đồ thị của hàm số không đi qua Q(1;2e+1). 
Câu 28. Cho hàm số 
3
2y x . Khẳng định nào sau đây đúng. 
A. Hàm số đồng biến trên R B. Hàm số có đạo hàm là 
3 x
2
C. Đồ thị hàm số có 2 đường tiệm cận D. Đồ thị hàm số luôn đi qua A(1;1) 
Câu 29. Tập xác định của hàm số    
1
2 2y x 2x 3 là: 
A. R B.  R \ 3;1 C.       ; 3 1; D.  0; 
Câu 30. Hàm số  2 2y ln(2x e ) có đạo hàm cấp 1 là: 
A. 
2 2 2
x
(2x e )
 B. 

2 2 2
4x 2e
(2x e )
 C. 
2 2
4x
2x e
 D. 
2 2 2
4x
(2x e )
Câu 31. Phương trình 
              
23x 2 x
7 11
11 7
 có nghiệm là: 
A.   x 1; x 2 B.  x 0;x 1 C.    x 1;x 2 D.  x 1; x 2 
Câu 32. Cho phép biến đổi:   x a
14 x log b
2
. Khi đó: 
A.  1a ; b 2
4
 B.  1a ; b 4
2
 C.   1a 4; b
2
 D.   1a 2; b
4
Câu 33. Cho phương trình:      2 2x x 1 x x 29 10.3 1 0 . Chọn phát biểu sai trong các phát biểu sau: 
A. Phương trình có 4 nghiệm 
B. Phương trình có hai nghiệm âm 
Gv: Nguyễn Văn Huy – 0968 64 65 97 Đề kiểm tra học kỳ 1 – Toán 12 
Trang 5 Tại liệu trắc nghiệm môn toán của học sinh lớp toán Thầy Huy – Biên Hòa, Đồng Nai 
C. Phương trình có hai nghiệm dương 
D.  x 1 là nghiệm của phương trình 
Câu 34. Anh Việt muốn mua một ngôi nhà trị giá 500 triệu đồng sau 3 năm nữa. Biết rằng lãi suất 
hàng năm vẫn không đổi là 8% một năm. Vậy ngay từ bây giờ số tiền ít nhất anh Việt phải 
gửi tiết kiệm vào ngân hàng theo thể thức lãi kép để có đủ tiền mua nhà (kết quả làm tròn 
đến hàng triệu) là 
A. 397 triệu đồng. B. 396 triệu đồng. C. 395 triệu đồng. D. 394 triệu đồng. 
Câu 35. Tập nghiệm của bất phương trình:    20,5 0,5log (5x 10) log (x 6x 8) là: 
A. x 4 B. x 2 C.  4 x 2 D.
    
x 4
x 2 
Câu 36. Tập nghiệm của bất phương trình      0.2 0.2log x 1 log 3 x là: 
A.  1;3 B.  1;3 C.  1; D.  ; 3 
Câu 37. Trong các khẳng định sau, khẳng định nào sai? 
A. 3log 5 0 B.  2 2x 2 x 2log 2016 log 2017 
C. 
      7 7
2log 5 log
7
 D. 0,75log 0,76 0 
Câu 38. Có thể phân chia khối lăng trụ tam giác ABC.A’B’C’ thành các khối tứ diện như: 
A. AA’B’C’ ; ACB’C ; A.B’CC’ B. AA’B’D’ ; ABB’C ; A.B’CC’ 
C. AA’B’C’ ; ABB’C ; A.B’DC’ D. AA’B’C’ ; ABB’C ; A.B’CC’ 
Câu 39. Số cạnh của một hình tứ diện đều là 
A. 4 B. 6 C. 8 D. 10. 
Câu 40. Trong các hình sau hình nào không phải là hình đa diện? 
A. B. C. D. 
Câu 41. Ba kích thước của một hình hộp chữ nhật lần lượt là x, 2x, 4x (x > 0). Thể tích của hình hộp 
đã cho là 1728. Khi đó x bằng: 
A. 4 B. 2 C. 3 D. 6 
Câu 42. Cho lăng trụ đứng ABC.A’B’C’có tất cả các cạnh đều bằng a .Thể tích của khối tứ diện 
A’.ABC bằng: 
A. 
3a 3
12
. B. 
3a 3
6
. C. 
3a 3
36
. D. 
3a 3
24
 . 
Câu 43. Cho hình chóp S.ABCD đáy là hình thoi với AC=2BD=2a và tam giác SAD vuông cân tại S 
nằm trong mp vuông góc với đáy.Thể tích khối chóp là: 
A. 
33a
12
 B. 
315a
24
 C. 
35a
12
 D. 
35a
4
Câu 44. Cho hình chóp S.ABCD, M là điểm trên SA mà SM=
1
3
 SA. Khi đó tỉ số SMBD
SABD
V
V
bằng: 
Gv: Nguyễn Văn Huy – 0968 64 65 97 Đề kiểm tra học kỳ 1 – Toán 12 
Trang 6 Tại liệu trắc nghiệm môn toán của học sinh lớp toán Thầy Huy – Biên Hòa, Đồng Nai 
A. 2 B. 3 C. 
1
2
 D. 
1
3
Câu 45. Kim tự tháp Kê-ốp ở Ai cập được xây dựng vào khoảng 2500 năm trước Công nguyên . 
Kim tự tháp này là một tứ giác đều có chiều cao 147m , cạnh đáy dài 230 m. Khi đó thể tích 
của Kim tự tháp bằng: 
A 7.776.300 m 3 B 2.592.100 m 3 C 2.592.100 m 2 D 7.776.300 m 2 
Câu 46. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở B , AC a 2 , SA a và 
vuông góc với đáy  ABC . Gọi G là trọng tâm tam giác SBC . Mặt phẳng   qua AG và 
song song với BC cắt SB , SC lần lượt tại M , N . Tính theo a thể tích khối chóp S.AMN . 
A. 
3
V 2a
27
. B. 
3
V 2a
29
. C. 
3
V a
9
. D. 
3
V a
27
. 
Câu 47. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với  AD 2AB 2a . Cạnh bên 
SA 2a và vuông góc với đáy. Gọi M, N lần lượt là trung điểm của SB và SD . Tính 
khoảng cách từ S đến mặt phẳng  AMN . 
A. 
a 6 .
3
 B. 2a. C. 3a .
2
 D. a 5. 
Câu 48. Diện tích hình tròn lớn của một hình cầu là p . Một mặt phẳng   cắt hình cầu theo một hình 
tròn có diện tích là 
p
2
. Khoảng cách từ tâm mặt cầu đến mặt phẳng   bằng: 
A. 
p
. B. 
1
. C. 
2p
. D. 
p
2
. 
Câu 49. Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng R 3. Diện tích xung 
quanh và diện tích toàn phần của hình lần lượt có giá trị là: 
A.    22 3 1 R và  22 3 R . B.  22 3 R và    22 3 1 R . 
C.  22 3 R và  22 R . D.  22 3 R và  2 22 3 R R . 
Câu 50. Cho mặt cầu tâm O , bán kính R a . Một hình nón có đỉnh là S ở trên mặt cầu và đáy là 
đường tròn tương giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng SO tại 
H sao cho  3aSH
2
. Độ dài đường sinh  của hình nón bằng: 
A.  a. B.  a 2. C.  a 3. D.  2a.