Đề thi học kì 1 môn thi: Toán – lớp 11 (Đề 1)

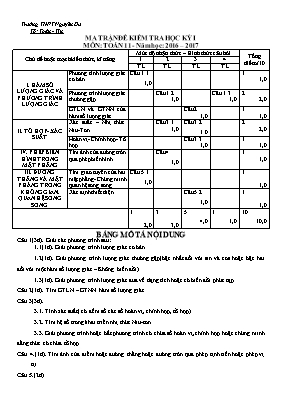
Trường THPT Nguyễn Du
 Tổ: Toán - Tin
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I
MÔN: TOÁN 11 - Năm học: 2016 – 2017 
Chủ đề hoặc mạch kiến thức, kĩ năng
Mức độ nhận thức – Hình thức câu hỏi
Tổng điểm /10
1
2
3
4
TL
TL
TL
TL
I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Phương tình lượng giác cơ bản
Câu 1.1
 1,0
1
1,0
Phương trình lượng giác thường gặp
Câu 1.2
 1,0
Câu 1.3
1,0
2
2,0
GTLN và GTNN của hàm số lượng giác
Câu 2
1,0
1
1,0
II. TỔ HỢP- XÁC SUẤT
Xác suất – Nhị thức Niu-Tơn
Câu 3.1
 1,0
Câu 3.2
 1.0
2
2,0
Hoán vị- Chỉnh hợp- Tổ hợp. 
Câu 3.3
1,0
1
1,0
IV. PHÉP BIẾN HÌNH TRONG MẶT PHẲNG
Tìm ảnh của đường tròn qua phép biến hình
Câu 4.
 1,0
1
 1,0
III. ĐƯỜNG THẲNG VÀ MẶT PHẢNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
Tìm giao tuyến của hai mặt phẳng- Chứng minh quan hệ song song
Câu 5.1
 1,0
1
1,0
Xác định thiết diện
Câu 5.2
 1,0
1
1,0
1
2,0
3
3,0
5
4,0
1
1,0
10
10,0
BẢNG MÔ TẢ NỘI DUNG
Câu 1(3đ). Giải các phương trình sau:
1.1(1đ). Giải phương trình lượng giác cơ bản.
1.2(1đ). Giải phương trình lượng giác thường gặp(bậc nhất đối với sin và cos hoặc bậc hai đối với một hàm số lượng giác – Không biến đổi).
1.3(1đ). Giải phương trình lượng giác đưa về dạng tích hoặc có biến đổi phức tạp.
Câu 2(1đ). Tìm GTLN – GTNN hàm số lượng giác.
Câu 3(3đ). 
3.1. Tính xác suất( có đếm số các số hoán vị, chỉnh hợp, tổ hợp).
3.2. Tìm hệ số trong khai triển nhị thức Niu-tơn.
3.3. Giải phương trình hoặc bất phương trình có chứa số hoán vị, chỉnh hợp hoặc chứng minh đẳng thức có chứa tổ hợp.
Câu 4.(1đ). Tìm ảnh của điểm hoặc đường thẳng hoặc đường tròn qua phép tịnh tiến hoặc phép vị tự.
Câu 5.(2đ)
5.1(1đ). Chứng minh quan hệ song song.
5.2.(1đ). Xác định thiết diện.
--------------------------------------------------------
Trường THPT Nguyễn Du
 Tổ: Toán - Tin
ĐỀ THI HỌC KÌ I NĂM HỌC 2016 - 2017
MÔN THI: TOÁN – LỚP 11
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
Câu 1. (3,0 điểm) Giải các phương trình sau:
	1) 
	2) 
	3) 
Câu 2.(1 điểm) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số :.
Câu 3. (3,0 điểm)
 1) Có 10 hoa hồng trong đó có 7 hoa hồng vàng và 3 hoa hồng trắng. Chọn ra 3 hoa hồng
để bó thành một bó. Tính xác suất để có ít nhất một hoa hồng trắng.
 2) Tìm số hạng không chứa x trong khai triển của 
	 3) Giải phương trình : 
Câu 4.(1 điểm) Cho đường tròn (C): và điểm I(–3; 2). Viết phương trình đường tròn (C¢) là ảnh của (C) qua phép vị tự tâm I tỉ số .
Câu 5. (2,0 điểm) Cho tứ diện ABCD .N, Q lần lượt là trung điểm của BC , BD. Gọi () là mặt phẳng chứa đường thẳng NQ và song song với AB
) Chứng minh NQ // (ACD) .
Hãy xác định thiết diện của mặt phẳng () với tứ diện ABCD
----------------Hết------------------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
Họ và tên học sinh:Số báo danh:
ĐÁP ÁN VÀ BIỂU ĐIỂM
MÔN: TOÁN 11 – HKI NĂM HỌC 2016 - 2017
CÂU
Ý
NỘI DUNG
ĐIỂM
1
 (3 đ)
1
(1đ)
 1.0
2
(1đ)
Phương trình đã cho tương đương phương trình sau:
Đặt t = cosx (đk : )
Ta có : 
Với t = –1 cosx = –1 (kZ)
Với t = cosx = x = arccos() + k2(kZ)
0.25
0.25
0.25
0.25
3
(1đ)
0.25
0.25
0.25
0.25
2(1đ)
Ta có: = 
 = 
	Þ (vì )
	Þ khi ;	 khi .	
 0.25
 0.25
0.5
3
 (3 đ)
1
(1đ)
Gọi A là biến cố “có ít nhất một hoa hồng trắng”, 
Suy ra : “ cả 3 hoa được chọn đều là hoa hồng vàng “
0.25
0.25
0.25
0.25
2
(1đ)
Theo giả thiết ta có : 
Vậy số hạng không chứa x là 
0.5
0.25
0.25
3
(1đ)
Điều kiện 
So sánh điều kiện ta thấy n=40 thỏa mãn.Vậy phương trình có nghiệm n=40
0.25
0.25
0.25
0.25
4(1đ)
Đường tròn (C): có tâm K(4; 0) và bán kính 
	Gọi và R¢ là tâm và bán kính của đường tròn ảnh (C¢).
	Þ và .
	Ta có: 
	Vậy phương trình của (C¢) là .
0.25
 0.25
 0.25
 0.25
5
(2 đ)
1
(1đ)
Ta có NQ (ACD)
 	 NQ // CD ( vì NQ là đường trung bình của tam giác BCD)
 CD (ACD)
Suy ra NQ // (ACD)
0.75
0.25
2
(1đ)
Ta có :	
	Mặt khác
	Từ (1) và (2), ta được : NP // MQ
	Vậy: thiết diện là hình thang MPNQ 
0.5
0.25
0.25
 Nếu học sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì cho đủ số điểm từng phần như hướng dẫn quy định
----Hết----