Đề thi giữa kì I môn Toán

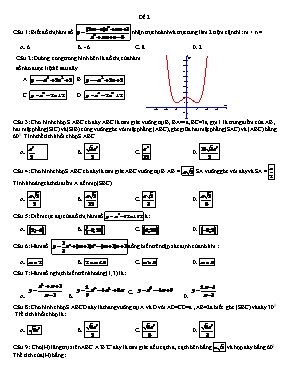
Đề 2
Câu 1: Biết đồ thị hàm số nhận trục hồnh và trục tung làm 2 tiệm cận thì : m + n =
A. 6	B. - 6	C. 8	D. 2
Câu 2: Đường cong trong hình bên là đồ thị của hàm số nào được liệt kê sau đây 
A. 	B. 	
C. 	D. 
Câu 3: Cho hình chĩp S.ABC cĩ đáy ABC là tam giác vuơng tại B, BA=4a, BC=3a, gọi I là trung điểm của AB , hai mặt phẳng (SIC) và (SIB) cùng vuơng gĩc với mặt phẳng (ABC), gĩc giữa hai mặt phẳng (SAC) và (ABC) bẳng 600. Tính thể tích khối chĩp S.ABC
A. 	B. 	C. 	D. 
Câu 4: Cho hình chĩp S.ABC cĩ đáy là tam giác ABC vuơng tại B. AB = . SA vuơng gĩc với đáy và SA = . Tính khoảng cách từ điểm A đến mp(SBC)
A. 	B. 	C. 	D. 
Câu 5: Điểm cực đại của đồ thị hàm số là:
A. 	B. 	C. 	D. .
Câu 6: Hàm số đồng biến trên tập xác định của nĩ khi :
A. 	B. 	C. 	D. 
Câu 7: Hàm số nghịch biến trên khoảng (1;3) là:
A. B. C. 	D. 
Câu 8: Cho hình chĩp S.ABCD đáy là thang vuơng tại A và D với AD=CD=a , AB=2a biết gĩc (SBC) và đáy 300 .Thể tích khối chĩp là:
A. 	B. 	C. 	D. 
Câu 9: Cho(H) lăng trụ xiên ABC.A’B’C’ đáy là tam giác đều cạch a, cạch bên bằng và hợp đáy bằng 600. Thể tích của (H) bằng:
A. 	B. 	C. 	D. 
Câu 10: Đường thẳng y = m khơng cắt đồ thi hàm số khi :
A. 	B. 	C. 	D. 
Câu 11: Cho (H) là khối lăng trụ đứng tam giác đều cĩ tất cả các cạnh bằng a. Thể tích bằng:
A. 	B. 	C. 	D. 
Câu 12: 
Đường cong trong hình bên là đồ thị bên là đồ thị của hàm số nào được liệt kê sau đây 
A. 	B. 	
C. 	D. 
Câu 13: Một chất điểm chuyển động theo quy luật .
 Thời điểm t (giây) tại đĩ vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất là :
A. t=3	B. t=1	C. t=2	D. t=4
Câu 14: Cho hình chĩp tam giác đều S.ABC cĩ cạnh đáy bằng a và chiều cao của hình chĩp là . Tính theo a thể tích khối chĩp S.ABC.
A. 	B. 	C. 	D. 
Câu 15: Cho hình chĩp tứ giác đều S.ABCD cĩ cạnh đáy bằng . Gĩc giữa cạnh bên và mặt đáy bằng 300.Tính theo a thể tích khối chĩp S.ABCD.
A. 	B. 	C. 	D. 
Câu 16. Giá trị của m để hàm số y = x3 – 2mx2 + (m + 3)x – 5 + m đồng biến trên R là:
	 B. 	 C. 	 D. 
Câu 17. Xác định m để hàm số y = nghịch biến trên R?
hoặc B. C. D. hoặc 
Câu 18. Tìm m để hàm số y = giảm trên từng khoảng xác định của nĩ?
 B. C. D. 
Câu 19. Hàm số y = đồng biến trên khoảng nào?
(; 1) B. (0 ; + ) C. (- 1 ; + ) D. (1 ; + ) 
Câu 20. Tìm m để hàm số y = x3 – 3(2m + 1)x2 + (12m + 5)x + 2 đồng biến trên khoảng (2 ; +) ? 
 B. C. D. 	
Câu 21. Giá trị của để hàm số y = x3 + 3(m - 2)x2 + 3x + m đồng biến trên khoảng (;1) là :
 B. m > 1 C. m > 3 D. m 3
Câu 22. Xác định m để hàm số y = x2(m – x) – m đồng biến trên khoảng (1 ; 2) ?
m > 3 	 B. m < 3	 C. D. 
Câu 23. Hàm số y = đồng biến trên từng khoảng xác định của nĩ khi:
	B. 	C. 	D. 
Câu 24. Hàm số y = nghịch biến trên khoảng:
	B. 	C. 	D. 
Câu 25. Hàm số y = đồng biến trên các khoảng:
 và ( 1 ; 2 )	C. ( 0 ; 1 ) và ( 1 ; 2 )
 và 	D. và 
Câu 26. Hàm số nào sau đây khơng cĩ cực trị?
y = x3 + 3x2 – 1 	B. y = 	C. y = - x4 + 1 D. y = - 2x + 
Câu 27. Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = là : 
y = x + 5	 B. y = 2x + 5	 C. y = 2x + 1	 D. y = 2x	
Câu 28. Biết đồ thị hàm số y = x3 – 3x2 + 1 cĩ hai điểm cực trị. Phương trình đường thẳng đi qua hai điểm cực trị là:
y = 2x – 1	B. y = -2x – 1	 C. y = 2x + 1	 D. y = -2x + 1
Câu 29. Biết đồ thị hàm số y = x3 – x2 – 2x + 1 cĩ hai điểm cực trị. Phương trình đường thẳng đi qua hai điểm cực trị là:
y = 3x + 5	B. y = - 3x – 5	 C. y = D. y = 
Câu 30. Biết khi m 1 thì hàm số y = x3 – 3mx2 + 3x + 2 cĩ hai cực trị, khi đĩ phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số là:
y = 2mx + m – 2	 C. y = - 2mx +3m - 1
y = 2( 1 + m2)x + m + 2	 D. y = 2( 1 - m2)x + m + 2
Câu 31. Cho hàm số y = x3 – mx2 + 3x + 1. Hàm số cĩ cực đại và cực tiểu khi :
-3 3
Câu 32. Hàm số y = mx4 + 2(m – 2)x2 – 1 cĩ 3 cực trị khi:
m 0	C. 0 < m < 2	D. 
Câu 33. Giá trị nào của m để điểm I(-1;6) là điểm cực đại của đồ thị hàm số y = x3 – 3mx2 – 9x + 1(Cm):
m = - 1	B. m = 	C. m = 1	D. m = 2
Câu 34. Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số y = x3 – 3x + 4 là:
4	B . 	C. 5	D. 
Câu 35. Cho hàm số y = . Để hàm số đạt cực trị tại x1, x2 thoả mãn 
x1 + 2x2 = 1, thì giá trị m cần tìm là:
m = 2 hay m = 	C. m = 1 hay m = 
m = -2 hay m = 	D. m = - 1 hay m = 
Câu 36. Giá trị m để đồ thị hàm số y = x4 + mx2 – 1 nhận điểm I(1 ; - 2) làm điểm cực tiểu là:
m = 2	B. m = - 2 	C. m = 1	D. m = 4
Câu 37. Đồ thị hàm số y = - x4 + 2mx2 cĩ 3 điểm cực trị tạo thành một tam giác đều khi:
m = 0	B. m = 0, m = 	C. m = 	D. m = 0, m = 27
Câu 38. GTLN của hàm số y = là:
2	B. 1	C. 	D. 3
Câu 39. GTNN và GTLN của hàm số y = x + là:
miny = - 2, maxy = 2	 	C. miny = - 2, maxy = 2
miny = 2, maxy = 2	D. miny = - 2, maxy = 2
Câu 40. Đồ thị hàm số y = - x3 + 3x2 + 9x + 2 cĩ tâm đối xứng là:
(1 ; 12)	B. (1 ; 0)	C. (1 ; 13)	D. (1 ; 14)
Câu 41. Số điểm uốn của đồ thị hàm số y = x4 – 6x2 + 3 là:
0	B. 1	C. 2	D. 3
Câu 42. Tâm đối xứng của đồ thị hàm số y = là : 
(1 ; 2)	B. (2 ; 1)	C. (1 ; -1)	D. (-1 ; 1)
Câu 43. Số giao điểm của đồ thị hàm số y = - x4 – 2x2 – 1 với trục Ox là:
1	B. 2 	C. 3	D. 0
Câu 44. Số giao điểm của đồ thị hàm số y = x3 – 4x và trục Ox là:
3	B. 2	C. 0	D. 4
Câu 45. Số giao điểm của đường cong y = x3 – 2x2 + 2x + 1 và đường thẳng y = 1 – x là:
3	B. 2	C. 1	D. 0
Câu 46. Đồ thị hàm số y = ax3 + bx2 – x + 3 cĩ điểm uốn là I(-2 ; 1) khi:
	B. 	C. 	D. 
Câu 47. Đồ thị của hàm số nào sau đây cĩ hình dạng như hình vẽ bên:
y = x3 – 3x + 1
y = - x3 + 3x + 1
y = - x3 – 3x + 1
Câu 48. Đường thẳng y = kx – 2 cắt đồ thị hàm số y = tại hai điểm phân biệt khi :
k hay k > 2	C. k hay k > 	
 hay k > 	D. k hay k > - 2 
Câu 49. Đồ thị ở hình 1 là đồ thị của hàm số nào sau đây:
y = x3 + 3x2 – x – 1
y = x3 – 2x2 + x – 2 
y = (x – 1)( x – 2)2	Hình 1
y = (x + 1)( x – 2)2
Câu 50. Đồ thị ở hình 2 là đồ thị của hàm số nào sau đây:
y = x3 + 3x2 – x – 1
y = - x3 – 2x2 + x – 2 
y = - x3 + 3x + 1	 	 	 Hình 2
y = x3 + 3x2 – x – 1
Câu 51. Đồ thị ở hình 3 là đồ thị của hàm số nào sau đây:
y = - x4 – 2x2 + 3
y = x4 – 2x2 - 3
y = - x4 – 2x2 - 3
y = x4 + 2x2 - 3	Hình 3
Câu 52. Đường thẳng y = mx + 2 cắt đồ thị hàm số y = tại hai điểm phân biệt khi và chỉ khi:
m 4	C. 0 4
Câu 53. Đường thẳng y = mx + 2 – m cắt đồ thị hàm số y = tại hai điểm phân biệt khi :
m > 	B. m 1, m 	C. m 	D. m 
Câu 54. Tiếp tuyến của đồ thị hàm số y = tại điểm uốn cĩ phương trình là:
y = - x + 	B. y = - x - 	C. y = x + 	D. y = x + 
Câu 55. Cho hàm số y = - x2 – 4x + 3 cĩ đồ thị là (P). Nếu tiếp tuyến tại M của (P) cĩ hệ số gĩc là 8 thì hồnh độ điểm M là:
12	B. - 6	C. – 1	D. 5
Câu 56. Tiếp tuyến của đồ thị hàm số y = ln( 1 + x2 ) tại điểm cĩ hồnh độ x = -1, cĩ hệ số gĩc bằng: 
ln2	B. – 1	C. 4	D. 0
Câu 57. Gọi M là giao điểm của đồ thị hàm số y = với trục Ox. Phương trình tiếp tuyến với đồ thị tại M là:
	B. 	C. 	D. 
Câu 58. Tiếp tuyến của đồ thị hàm số y = song song với đường thẳng 2x + y – 5 = 0 cĩ phương trình là:
2x + y - = 0 và 2x + y – 2 = 0	C. 2x + y + = 0 và 2x + y + 2 = 0
2x + y – 4 = 0 và 2x + y – 1 = 0	D. 2x + y – 3 = 0 và 2x + y + 1 = 0
Câu 59. Tiếp tuyến của đồ thị hàm số y = x3 – 3x2 – 3x vuơng gĩc với đường thẳng x + 6y – 6 = 0 cĩ phương trình là:
y = 6x + 6 và y = 6x + 12	C. y = 6x + 5 và y = 6x - 27
 y = 6x – 5 và y = 6x + 27	D. y = 6x – 6 và y = 6x – 12
Câu 60. Cho hàm số y = (C). Tìm điểm M thuộc đồ thị (C), biết tiếp tuyến của (C) tại M cắt Ox, Oy tại hai điểm A, B và OAB cĩ diện tích bằng .
M(1 ; 1) hoặc M	B. M(1 ; - 2)	C. M(0 ; 3)	D. M( 2 ; 2)
ĐỀ ƠN TẬP TỔNG HỢP THI THỬ THPTQG LẦN 1
Hàm số nghịch biến trên các khoảng: A. 	B. 	C. 	D. .
Hàm số nào sau đây nghịch biến trên R
A. B. 	C. 	D. 
Từ đồ thị hàm số sau suy ra khoảng đồng biến của hàm số là
 và 	B. và 	C. và 	D. và 
Tìm m để hàm số đồng biến trên từng khoảng xác định.
A.	B. 	C. 	D. 
hàm số . luơn đồng biến trên với m
A.	B. 	C.m0	D.khơng cĩ giá trị m
hàm số . luơn đồng biến trên trên khoảng với m
A. .	B. 	C. 	D. 
Trong các khẳng định sau về hàm số , khẳng định nào là đúng?
A. Hàm số đạt cực tiểu tại x = 0; B. Hàm số đạt cực đại tại x = 1;
C. Hàm số đạt cực đại tại x = -1; D. Cả 3 câu trên đều đúng. 
Số điểm cực đại của hàm số là A.0	B. 1	C. 2	D. 3
. Toạ độ điểm cực đại của hàm số là A. (-1;2) B. (1;2) C. D. (1;-2)
Cho hàm số . Để hàm số cĩ cực đại và cực tiểu, điều kiện cho tham số m là:
A. m 1	B. m 2	C. -2 < m <1	D. -1 < m < 2
Cho hàm số . Để hàm số đạt cực trị tại , thỏa mãn thì giá trị cần tìm của m là: 
A. m = 2 hay m = 2/3	B. m = -1 hay m = -3/2 C. m = 1 hay m = 3/2	D. m = -2 hay m = -2/3
Đồ thị hàm số cĩ 3 điểm cực trị thì tập giá trị của m là:
A. 	B. 	C. 	D. 
Cho hàm số . Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bằng:
A. 	B. 4	C. 	D. 
Cho hàm số . Chọn phương án đúng trong các phương án sau	
A. 	B. C. D. 
Cho hàm số , giá trị nhỏ nhất của hàm số trên bằng 2 khi
A . 	B. 	C. 	D. 
Cho hàm số , chọn phương án đúng A. 	
a = 0	B. a= 1; a= 8	C. a = 0, a= 8	D. a = 8
Cho đồ thi hàm số ( C ) . Gọi là hồnh độ các điểm M ,N 
trên ( C ), mà tại đĩ tiếp tuyến của ( C ) vuơng gĩc với đường thẳng y = - x + 2016 . Khi đĩ là:
A. 	B. 	C. 	D. -1
Cho (Cm):y=. Gọi A(Cm) có hoành độ là -1. Tìm m để tiếp tuyến tại A song song với (d):y= 5x ? A. m= -4 B. m=4 C. m=5 D. m= -1
Cĩ thể chia hình lập phương thành bao biêu tứ diện bằng nhau? 
A. Hai	 B. Vơ số C. Bốn	D. Sáu
Cho (H) là khối chĩp tứ giác đều cĩ tất cả các cạnh bằng a. Thể tích của (H) bằng:
A. 	B. 	C. 	D. 
Trong các mệnh đề sau, mệnh đề nào sai? 
 A. Hình lập phương là đa điện lồi. B. tứ diện là đa diện lồi
C. Hình hộp là đa diện lồi . D. Hình tạo bởi hai tứ diện đều ghép với nhau là một đa diện lồi
Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau:
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh . B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt . D. Mỗi mặt cĩ ít nhất ba cạnh
Hình lập phương cĩ mấy mặt phẳng đối xứng 
 A. 4	B. 6 	C. 8	D. 12
Cho lăng trụ tam giác ABC. A’B’C’ cĩ thể tích là V. M, N lần lượt là trung điểm của A’C’ và BC. Tính thể tích của tứ diện MABN
 V/6	B. V/3 C. V/2	V/4
Cho hình chĩp tam giác đều S.ABC cĩ cạnh AB bằng a. Các cạnh bên SA, SB, SC tạo với đáy một 
 gĩc 600. Gọi D là giao điểm của SA với mặt phẳng qua BC và vuơng gĩc với SA. Tính tỉ số thể tích của hai khối chĩp S.DBC và S.ABC
3/8	B. 5/8	C. 1/8	D. 2/3
Cho hình lập phươngcạnhbằng a. Khoảng cáchgiữavàbằng