Đề thi giữa học kỳ I môn Toán Lớp 12

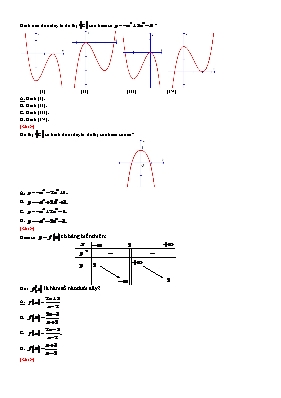
Hình nào dưới đây là đồ thị của hàm số ?
 (I) (II) (III) (IV)
A. Hình (I).
B. Hình (II).
C. Hình (III).
D. Hình (IV).
[]
Đồ thị có hình dưới đây là đồ thị của hàm số nào?
A. 
B. 
C. 
D. 
[]
Hàm số có bảng biến thiên:
Hỏi là hàm số nào dưới đây?
A. .
B. .
C. 
D. .
[]
Các khoảng nghịch biến của hàm số là
A. (-∞; 1) và (1; +∞).
B. (-∞; 1).	
C. (1; +∞).	
D. (-∞; +∞).
[]
Cho hàm số . Trong các mệnh đề sau, tìm mệnh đề đúng?
A. Hàm số tăng trên khoảng .
B. Hàm số tăng trên khoảng .
C. Hàm số tăng trên khoảng .
D. Hàm số giảm trên khoảng .
[]
Cho hàm số . Trong các mệnh đề sau, tìm mệnh đề đúng?
A. Hàm số có một cực trị trên R .
B. Hàm số không có cực trị trên R. 
C. Hàm số có hai cực trị trên R.
D. Hàm số có ba cực trị trên R.
[]
Cho hàm số . Tổng hai giá trị cực trị bằng 
A. 72.
B. 62.
C. 52.
D. 42.
[]
Hàm số đạt cực tiểu tại khi
A. .	
B. .	
C. .
D. .	
[]
Tìm để hàm số có ba điểm cực trị lập thành một tam giác đều.
A. .	
B. .	
C. .
D. .
[]
Giá trị nhỏ nhất của hàm số trên đoạn bằng
A. .	
B. .	
C. .
D. .
[]
Giá trị lớn nhất của hàm số trên đoạn bằng
A. 	
B. 	
C. 
D. 
[]
Tìm để đồ thị hàm số nhận đường thẳng làm tiệm cận ngang?
A. .	
B. .	
C. .
D. .
[]
Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ là
A. .	
B. .	
C. .
D. .
[]
Tính đạo hàm của hàm số .
A. .	
B. .	
C. .
D. .
[]
Cho hàm số có đồ thị . Tìm tọa độ điểm trên có hoành độ dương, sao cho tiếp tuyến với tại có hệ số góc bằng 2.
A. .	
B. .	
C. .
D. .
[]
Cho hàm số . Xét các mệnh đề sau:
	I. Hàm số đạt cực đại tại và đạt cực tiểu tại .
	II. Hàm số đạt cực đại tại và đạt cực tiểu tại .
	III. Hàm số đồng biến trên và nghịch biến trên các khoảng .
	IV. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng .
Mệnh đề nào đúng?
A. Chỉ II và III.
B. Chỉ I và III.
C. Chỉ I và IV.
D. Chỉ II và IV.
[]
Đồ thị hàm số cắt đường thẳng tại mấy điểm?
A. .	
B. .	
C. .
D. Không cắt nhau.
[]
Cho hàm số có đồ thị và đường thẳng . Tìm để đồ thị cắt đường thẳng tại 2 điểm phân biệt?
A.  R.	
B. .	
C. .
D. .
[]
Tọa độ giao điểm của đồ thị của hàm số và trục hoành là:
A. .	
B. .	
C. .
D. .
[]
Cho hàm số có đồ thị là , đường thẳng . Tìm các giá trị dương của tham số để đường thẳng cắt tại ba điểm phân biệt sao .
A. .	
B. .	
C. .
D. .
[]
Tập xác định của hàm số là
A. .	
B. .	
C. .
D. .
[]
Tập xác định của hàm số là
A. .	
B. .	
C. .
D. .
[]
Giá trị biểu thức ( với ) bằng
A. .	
B. .	
C. .
D. .
[]
Tập nghiệm của phương trình là
A. .	
B. .	
C. .
D. .
[]
Tổng hai nghiệm của phương trình là
A. .	
B. .	
C. .
D. .
[]
Nghiệm của phương trình là
A. Phương trình vô nghiệm.	
B. .	
C. .
D. .
[]
Trong không gian, đáy của hình chóp là hình vuông có độ dài đường chéo bằng . Cạnh bên vuông góc với mặt phẳng đáy và có độ dài là . Thể tích của khối chóp tính theo a bằng
A. .	
B. .	
C. .
D. .
[]
Trong không gian, cho hình lăng trụ đứng có mặt đáy là tam giác vuông cân tại và . Cạnh A’C hợp với mặt phẳng đáy một góc bằng . Thể tích của khối lăng trụ tính theo a bằng 
A. . 
B. . 
C. .
D. . 
 []
Trong không gian, cho hình chóp có đáy là tam giác vuông cân tại . Cạnh bên vuông góc với mặt phẳng đáy và . Số đo góc tạo bởi mặt phẳng và mặt phẳng đáy bằng
A. .
B. .	
C. .
D. Đáp án khác.
[]
Cho hình chóp có đáy là hình vuông cạnh , vuông góc mặt phẳng đáy. Cạnh hợp với đáy một góc , gọi là khoảng cách từ điểm đến mặt phẳng . Tỉ số bằng
A. .
B. .
C. .
D. .
 []