Đề thi giải toán trên máy tính cầm tay lớp 9 cấp trường THCS Kỳ Thượng năm học 2015 - 2016

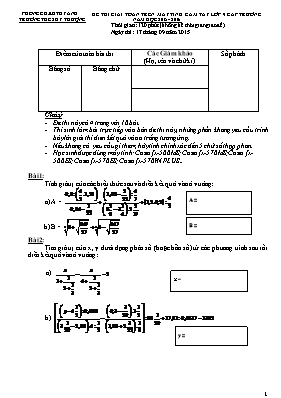
 PHÒNG GD&ĐT KỲ ANH ĐỀ THI GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY LỚP 9 CẤP TRƯỜNG
TRƯỜNG THCS KỲ THƯỢNG NĂM HỌC 2015 - 2016
Thời gian: 120 phút (không kể thời gian giao đề)
Ngày thi: 17 tháng 09 năm 2015 	
Điểm của toàn bài thi
Các Giám khảo
(Họ, tên và chữ kí)
Số phách
Bằng số
Bằng chữ
Chú ý: 
Đề thi này có 4 trang với 10 bài.
Thí sinh làm bài trực tiếp vào bản đề thi này, những phần không yêu cầu trình bày lời giải thì điền kết quả vào ô trống tương ứng. 
Nếu không có yêu cầu gì thêm, hãy tính chính xác đến 5 chữ số thập phân. 
Học sinh được dùng máy tính: Casio fx-500MS; Casio fx-570MS; Casio fx-500ES; Casio fx-570ES; Casio fx-570VN PLUS..
Bài 1: 
Tính giá trị của các biểu thức sau và điền kết quả vào ô vuông:
A = 
B = 
 	a) A = 	 KQ: 
 b) B = 
Bài 2: 
Tìm giá trị của x, y dưới dạng phân số (hoặc hỗn số) từ các phương trình sau rồi điền kết quả vào ô vuông :
x =
 a) 
y = 
b) 
Bài 3: 
b = 
a = 
a) Tìm các số tự nhiên a và b biết rằng	: 
b) Tìm số tự nhiên lớn nhất, nhỏ nhất (tương ứng đặt là a, b) có dạng chia hết cho 7
Sơ lược cách giải
Kết quả
a=
b=
Bài 4: Tìm số dư trong các phép chia sau:
 a) 11223344 : 2015 b) 12345678917092015 : 2015
Sơ lược cách giải
Kết quả
a)
b)
Bài 5: Cho đa thức và g(x) = x + 3
	Tìm hệ số a để 
Sơ lược cách giải
Kết quả
a=
Bài 6: Cho đa thức P(x) = . 
Biết P(1) = 3, P(2) = 9, P(3) = 19, P( 4) = 33, P(5) = 51. Tính giá trị P(6), P(7), P(8), P(9), P(10).
Sơ lược cách giải
Kết quả
Bài 7: Tính giá trị của biểu thức: 
	.
Sơ lược cách giải
Kết quả
Bài 8: Cho dãy số sắp với thứ tự U1 = 2; U2 = 20 và từ U3 trở đi được tính theo công thức (với ).
Viết quy trình bấm phím liên tục để tính giá trị Un với U1 = 2; U2 = 20.
Sử dụng quy trình trên để tính U23; U24; U25
Sơ lược cách giải
Kết quả:
Bài 9: 
Cho tam giác ABC có AB = 8,91cm ; AC = 10,32cm và . Tính:
Độ dài đường cao BH.
Diện tích tam giác ABC.
Độ dài cạnh BC. 
Cách giải:
Điền kết quả vào ô dưới:
BH = 
SABC = 
BC = 
Bài 10: Cho tam giác ABC có độ dài ba cạnh là AB = 3,06955cm; BC = 7,96305cm; CA = 5,50936cm. Gọi I và K theo thứ tự là chân đường vuông góc hạ từ A đến các đường phân giác của các góc B và góc C. Tính IK.
Sơ lược cách giải
Vẽ hình
 PHÒNG GD&ĐT KỲ ANH h­íng dÉn chÊm thi GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY LỚP 9 CẤP TRƯỜNG
TRƯỜNG THCS KỲ THƯỢNG NĂM HỌC 2015 - 2016
Thời gian: 120 phút (không kể thời gian giao đề )
Ngày thi: 17 tháng 09 năm 2015 	
Bài 1: (2 điểm)
Tính giá trị của các biểu thức sau và điền kết quả vào ô vuông:
 Mỗi câu đúng 1 điểm
A = 2 
B = 3 
 	a) A = 	 KQ: 
 b) B = 
Bài 2: (2điểm)
Tìm giá trị của x, y, z dưới dạng phân số (hoặc hỗn số) từ các phương trình sau rồi điền kết quả vào ô bên cạnh : Mỗi câu đúng 1 điểm
x =
 a) 
y = 6
b) 
Bài 3: (2 điểm) Mỗi câu đúng 1 điểm
b = 5
a = 8
a) Ta có: 
b)T×m sè tù nhiªn lín nhÊt, nhá nhÊt (t­¬ng øng ®Æt lµ a, b) cã d¹ng chia hÕt cho 7
C¸ch gi¶i
KÕt qu¶
Gi¶ sö sè lín nhÊt cã d¹ng lµ , khi ®ã ta ph©n tÝch = 192900+=7.27557+1+
Tõ ®ã suy ra z=4 
a =192934
Gi¶ sö sè nhỏ nhÊt cã d¹ng lµ , khi ®ã ta ph©n tÝch = 102000+3+=7.14571+3+
Tõ ®ã suy ra z=2 
b=102032
Bài 4: (2 điểm) Mỗi câu đúng 1 điểm 
Tìm số dư trong các phép chia sau: a) 11223344 : 2015; b) 12345678917092015 : 2015
Bấm 11223344 
 :
 2015 
=
 máy hiện thương số là 5 569,897767
Đưa con trỏ lên dòng biểu thức sửa lại là
11223344 –
 2015 . 
 5569 
=
 kết quả: 1809
b)Ta tìm số dư của phép chia 1234567891 cho 2015 được kết quả là 1571
Tìm tiếp số dư của phép chia 1571709201 cho 2015 kết quả là 1141
Tìm tiếp số dư của phép chia 11415 cho 2015 kết quả cuối cùng là 1340
 kết quả: 1340
Bài 5: (1,25 điểm) Cho đa thức và g(x) = x + 3
	Tìm hệ số a để 
Sơ lược cách giải
Kết quả
Đặt . Ta có 
bấm máy theo quy trình: 2 
ALPHAA
X
Shift
x3
 –
 3 
ALPHAA
X
x2
+
ALPHAA
X
 –
 1 
CALC
 (–)
 3 
=
 :
 2 
ab/c
 1 
ab/c
 3 
=
Bài 6:(1,25 điểm) Cho đa thức P(x) = . 
Biết P(1) = 3, P(2) = 9, P(3) = 19, P( 4) = 33, P(5) = 51. Tính giá trị P(6), P(7), P(8), P(9), P(10).
Sơ lược cách giải
Kết quả
Đặt Q(x) = . Khi đó Q(1) =3, Q(2) = 9 ; 
Q(3) = 19; Q( 4) = 33; Q( 5) = 51.
Vậy R(x) = P(x) – Q(x) c ó 5 nghi ệm 1; 2; 3; 4; 5.
V ậy P(x) = Q(x) + ( x – 1) ( x- 2) (x – 3) ( x- 4)( x- 5)
= + ( x – 1) ( x- 2) (x – 3) ( x- 4)( x- 5)
P(6) = 193 ; 
P(7)= 819;
 P(8) = 2649; P(9)= 6883 ; P(10)= 15321
Bài 7: (1,5 điểm) Tính giá trị của biểu thức: 
	.
Sơ lược cách giải
Kết quả
Áp dụng công thức tổng quát : để viết từng số hạng của M và thực hiện phép khử liên tiếp, cuối cùng ta được : 	
M 2014,4995
Bài 8:(2 điểm) Cho dãy số sắp với thứ tự U1 = 2; U2 = 20 và từ U3 trở đi được tính theo công thức (với ).
Viết quy trình bấm phím liên tục để tính giá trị Un với U1 = 2; U2 = 20.
Sử dụng quy trình trên để tính U23; U24; U25
Bấm 2 = à20=
Bấm Ans x 2 + anpha Ans(preAns)
Bấm = liên tiếp để tính Un
(1,0 điểm)
Kết quả:
U23 = 1941675090
U24 = 4687618336
(0,5 điểm)
U25 = 11316911762
 (0,5 điểm)
Bài 9: (4điểm)Cho tam giác ABC có AB = 8,91cm ; AC = 10,32cm và . Tính:
Độ dài đường cao BH.
Diện tích tam giác ABC.
Độ dài cạnh BC
 Sơ lược cách giải:
Ta có BH = AB Sin = 8,91.sin720 
= 8,47391 cm 	 (1,5 ñieåm)đ
SABC = AC.BH = 10,32.8.474 
= 43,72539 cm2	(1 ñieåm)đ
Ta có AH = AB. cos = 8,91.cos720 
 Suy ra HC = AC – AH = 10,32 - 8,91.cos720
 Do đó BC = (1,5 ñieåm)đ
BH = 8,47391 cm
SABC = 43,72539 cm2
BC = 11,36053 cm 
Bài 10: (2 điểm) Cho tam giác ABC có độ dài ba cạnh là AB = 3,06955cm; BC = 7,96305cm; CA = 5,50936cm. Gọi I và K theo thứ tự là chân đường vuông góc hạ từ A đến các đường phân giác của các góc B và góc C. Tính IK.
 A
c
b
I
K
F
a
E
B
C
DABI = DFBI (g.c.g) Þ AB = BF
 AI = IF (1)
DACK = DECK (g.c.g) Þ AC = CE
 AK = EK (2)
(1), (2) Þ IK là đường trung bình của DAEF, nên IK = EF
Mà EF = BF - BE = BF - BE + EC - EC = AB + AC – BC = b + c - a.
Do đó IK = = (cm)