Đề thi chọn học sinh giỏi lớp 9 cấp huyện năm học 2012- 2013 môn thi: Vật lý

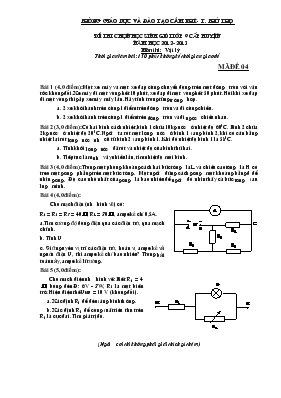
 Phòng Giáo dục và đào tạo Cẩm Khê- T. Phú thọ
 Đề thi chọn học sinh giỏi lớp 9 cấp huyện 
 năm học 2012- 2013
 Môn thi: Vật lý
 Thời gian làm bài: 150 phút không kể thời gian giao đề
MÃ ĐỀ 04
Bài 1 (4,0 điểm): Một xe máy và một xe đạp cùng chuyển động trên một đường tròn với vận tốc không đổi. Xe máy đi một vòng hết 10 phút, xe đạp đi một vòng hết 50 phút. Hỏi khi xe đạp đi một vòng thì gặp xe máy mấy lần. Hãy tính trong từng trường hợp.
a. 2 xe khởi hành trên cùng 1 điểm trên đường tròn và đi cùng chiều.
b. 2 xe khởi hành trên cùng 1 điểm trên đường tròn và đi ngược chiều nhau.
Bài 2 (3,0 điểm): Có hai bình cách nhiệt, bình 1 chứa 10kg nước ở nhiệt độ 600C. Bình 2 chứa 2kg nước ở nhiệt độ 200C. Người ta rót một lượng nước ở bình 1 sang bình 2, khi có cân bằng nhiệt lại rót lượng nước như cũ từ bình 2 sang bình 1. Khi đó nhiệt độ bình 1 là 580C.
	a. Tính khối lượng nước đã rót và nhiệt độ của bình thứ hai.
	b. Tiếp tục làm như vậy nhiều lần, tìm nhiệt độ mỗi bình.
Bài 3 (4,0 điểm): Trong một phòng khoảng cách hai bức tường là L và chiều cao tường là H có treo một gương phẳng trên một bức tường. Một người đứng cách gương một khoảng bằng d để nhìn gương. Độ cao nhỏ nhất của gương là bao nhiêu để người đó nhìn thấy cả bức tương sau lưng mình.
Bài 4 (4,0 điểm): 
 Cho mạch điện (như hình vẽ) có: 
R1 = R2 = R3 = 40, R4 = 30, ampe kế chỉ 0,5A.
a.Tìm cường độ dòng điện qua các điện trở, qua mạch chính.
b. Tính U
c. Giữ nguyên vị trí các điện trở, hoán vị ampe kế và nguồn điện U, thì ampe kế chỉ bao nhiêu? Trong bài toán này, ampe kế lí tưởng.
Bài 5 (5,0 điểm):
 Cho mạch điện như hình vẽ: Biết R1 = 4, bóng đèn Đ: 6V - 3W, R2 là một biến trở. Hiệu điện thế UMN = 10 V (không đổi). 
 a. Xác định R2 để đèn sáng bình thường.
 b. Xác định R2 để công suất tiêu thụ trên R2 là cực đại. Tìm giá trị đó. 
(Người coi thi không phải giải thích gì thêm)
hướng dẫn chấm thi h.s.g môn vật lý - lớp 9 
huyện cẩm khê năm học 2012 - 2013
Bài 1 (4,0 điểm):
Nội dung
Thang điểm
Gọi vận tốc của xe đạp là v đ vận tốc của xe máy là 5v 
Gọi t là thời gian tính từ lúc khởi hành đến lúc 2 xe gặp nhau. 
đ (0 < t 50); gọi C là chu vi của đường tròn.
0,5
a. Khi 2 xe đi cùng chiều.
	Quảng đường xe máy đi được: S1 = 5v.t	 
	Quảng đường xe đạp đi được: S2 = v.t	 
	Ta có: S1 = S2 + n.C
	Với C = 50v; n là lần gặp nhau thứ n, n N* 
1,0
đ 5v.t = v.t + 50v.n Û 5t = t + 50n Û 4t = 50n Û t = 	 
	Vì 0 < t 50 đ 0 < 50 Û 0 < 1	 
	Û n = 1, 2, 3, 4. Vậy 2 xe sẽ gặp nhau 4 lần
1,0
b. Khi 2 xe đi ngược chiều.
	Ta có: S1 + S2 = m.C (m là lần gặp nhau thứ m, mẻ N*)	 
	đ 5v.t + v.t = m.50v	 
	Û 5t + t = 50m Û 6t = 50m Û t = m 
1,0
Vì 0 < t 50 đ 0 <m 50	 
Û 0 < 1 Û m = 1, 2, 3, 4, 5, 6. Vậy 2 xe sẽ gặp nhau 6 lần.
0,5
Bài 2 (3,0 điểm):
Nội dung
Thang điểm
a) Gọi khối lượng nước rót là m(kg); nhiệt độ bình 2 là t2 ta có:
Nhiệt lượng thu vào của bình 2 là:	Q1 = 4200.2(t2 – 20)	
Nhiệt lượng toả ra của m kg nước rót sang bình 2:	Q2 = 4200.m(60 – t2)
0,5
Do Q1 = Q2, ta có phương trình:
4200.2(t2 – 20) = 4200.m(60 – t2)
 => 2t2 – 40 = m (60 – t2)	 (1)
0,5
ở bình 1 nhiệt lượng toả ra để hạ nhiệt độ:
	Q3 = 4200(10 - m)(60 – 58) = 4200.2(10 - m)	 
Nhiệt lượng thu vào của m kg nước từ bình 2 rót sang là;
	Q4 = 4200.m(58 – t2)	
0,5
Do Q3 = Q4, ta có phương trình:
	4200.2(10 - m) = 4200.m (58 – t2)	 
 => 2(10 - m) = m(58 – t2)	 (2)	
0,5
Từ (1) và (2) ta lập hệ phương trình:
Giải hệ phương trình tìm ra t2 = 300 C; m = 	
0,5
b) Nếu đổ đi lại nhiều lần thì nhiệt độ cuối cùng của mỗi bình gần bằng nhau và bằng nhiệt độ hỗn hợp khi đổ 2 bình vào nhau.	 
gọi nhiệt độ cuối là t ta có: Qtoả = 10. 4200(60 – t)	
Qthu = 2.4200(t – 20); Qtoả = Qthu => 5(60 – t) = t – 20
	=> t 53,30C
0,5
Bài 3 (4,0 điểm):
Nội dung
Thang điểm
1,0
Dựng B’C’ là ảnh của BC qua gương. Để người quan sát nhìn thấy cả bức tường sau gương thì mắt phải đồng thời nhìn thấy ảnh B’ và C’. Muốn vậy mắt M phải đón nhận được các tia phản xạ từ gương của các tia tới xuất phát từ B và C. Gọi I, K lần lượt là giao điểm của B’M và C’M với AD. Do đó chiều cao nhỏ nhất của gương là đoạn IK.
1,0
Ta có (1)
0,5
 (2)
0,5
Từ (1) và (2) , áp dụng tính chất dãy tỷ số bằng nhau ta được: 
Vậy chiều cao nhỏ nhất của gương: 
1,0
Bài 4 (4,0 điểm):
Nội dung
Thang điểm
a. Tớnh cường độ dũng điện :
0,5
Do R1 = R2 và mắc // với nhau nờn I1 = I2 (1)
R123 = = = 60; R4 = 30 
0,5
 I4 = 2 I123 = 2 I12 = 2.( I1 + I2 ) (2)
Số chỉ của ampe kế : IA = I2 + I4 = 0,5 A (3)
0,5
Từ (1) (2) (3) ta cú: 	I1 = 0,1 A 	I3= 0,2 A 	0,25đ
	I2 = 0,1 A	I4= 0,4 A	0,25đ
	 ITĐ = 0,6 A
1,0
b. Hiệu điện thế : U = I4 . R4 = 0,4 . 30 = 12 V
0,5
c. Hoỏn đổi vị trớ ampe kế và nguồn U : 
Ta cú : IA = I3 + I4
I4 = A
I3 = 0,1 A
 IA = 0,5 A
1,0
Bài 5 (5,0 điểm):
Nội dung
Thang điểm
Sơ đồ mạch: R1 nt (Rđ // R2).
Từ CT: P = đ Rđ = = = 12()	đ Iđ = = = 0,5 (A)
0,5
a. Để đèn sáng bình thường đ Uđ = 6v, Iđ = 0,5(A).
 Vì Rđ // R2 đ RAB = ; UAB = Uđ = 6v.	
 đ UMA = UMN – UAN = 10 – 6 = 4v	
0,5
Vì R1 nt (Rđ // R2) đ = = = đ 3RMA = 2RAN.	đ = 3.4 đ 2.R2 = 12 + R2 đ R2 = 12	Vậy để đèn sáng bình thường R2 = 12
1,0
b. 	Vì Rđ // R2 đ R2đ = đ Rtđ = 4 + = 
0,5
áp dụng định luật Ôm: I = = .	
Vì R nt R2đ đ IR = I2đ = I = đ U2đ = I.R2đ = .
0,5
áp dụng công thức: P=đP2 = = = 
Chia cả 2 vế cho R2 đ P2 = 	
0,5
 Để P2 max đ đạt giá trị nhỏ nhất
 đ đạt giá trị nhỏ nhất
0,5
áp dụng bất đẳng thức Côsi ta có: 
 + 162.R2 2. = 2.48.16 đ P2 Max ==4,6875 (W).	
0,5
Đạt được khi: = 162.R2 đ R22 = = 32 đ R2 = 3 	
Vậy khi R2 = 3 thì công suất tiêu thụ trên R2 là đạt giá trị cực đại.
0,5
Hết