Đề tham khảo thi tốt nghiệp quốc gia môn Toán

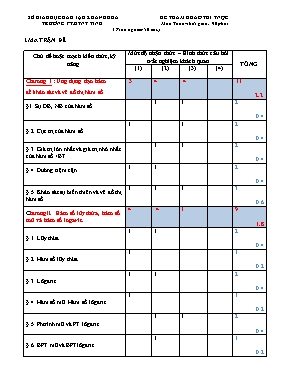
SỞ GIÁO DỤC ĐÀO TẠO KHÁNH HÒA
ĐỀ THAM KHẢO THI TNQG
TRƯỜNG PT.DTNT TỈNH
Môn Toán- thời gian : 90 phút
 ( Trắc nghiệm 50 câu )
I.MA TRẬN ĐỀ 
Chủ đề hoặc mạch kiến thức,kỹ năng 
Mức độ nhận thức – Hình thức câu hỏi trắc nghiệm khách quan
TỔNG
(1)
(2)
(3)
(4)
Chương I : Ứng dụng đạo hàm
 3
4
 4
 11
 2.2
để khảo sát và vẽ đồ thị hàm số
§1. Sự ĐB, NB của hàm số
1
1
2
 0.4
§ 2. Cực trị của hàm số
1
1
2
 0.4
§ 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số +BT
1
1
2
 0.4
§ 4. Đường tiệm cận
1
1
2
 0.4
§ 5. Khảo sát sự biến thiên và vẽ đồ thị hàm số
1
1
1
3
 0.6 
ChươngII. Hàm số lũy thừa, hàm số mũ và hàm số logarit.
4
 4
1
9
 1.8
§ 1. Lũy thừa
1
1
2
 0.4
§ 2. Hàm số lũy thừa
1
1
 0.2
§ 3. Lôgarit
1
1
2
 0.4
§ 4. Hàm số mũ. Hàm số lôgarit
1
1
 0.2
§ 5. Phtrình mũ và PT lôgarit
1
1
2
 0.4
§ 6. BPT mũ và BPTlôgarit
1
1
 0.2
Chương III. Nguyên hàm. Tích phân và ứng dụng.
2
4
1
7
 1.4
Nguyên hàm
1
1
0.2
Tích phân
1
2
1
4
0.8
Ứng dụng của tích phân trong hình học
2
2
0.4
Chương IV. Số phức.
2
2
 4
 0.8
§ 1. Số phức
1
1
2
0.4
§ 2. Cộng, trừ và nhân số phức
§ 3. Phép chia số phức
1
1
 0.2
§4.Ph.trình bậc 2với hệ số thực
1
1
 0.2
Chương I :. Khối đa diện
3
 3
1
7
 1.4
§ 1. Khái niệm về khối đa diện
1
1
 0.2
§ 2. Khối đa diện lồi và khối đa diện đều
1
1
2
 0.4
§ 3. Khniệm về thể tích khối đa diện
1
2
1
4
 0.8
Chương II. Mặt nón, mặt trụ, mặt cầu
1
 1
1
 3
 0.6
§ 1. Khái niệm về mặt tròn xoay
1
1
 0.2
§ 2. Mặt cầu
1
1
2
 0.4
Chương III. Phương pháp tọa độ trong không gian
4
3
2
9
 1.8
§ 1. Hệ tọa độ trong kg
1
1
4
 0.8
§ 2.Phương trình mặt phẳng
1
1
1
3
 0.6
§3.P.tr đường thẳng trong KG
2
1
1
4 
 0.8
Tổng số câu
Tổng điểm
Tỉ lệ
18
 3.6
 36%
22
 4.4
 44%
10
 2.0
 20%
50 
 10.00 
 100%
ĐỀ:
Sự ĐB, NB của hàm số
Thông hiểu
Câu 1: Hàm số nghịch biến khi x thuộc khoảng nào sau đây:
A (-2;0) 	B (-3;0)	C 	D. 
Vận dụng thấp
Câu 2: Hàm số đồng biến trên từng khoảng xác định khi:
A m1	B. m1 D. -1<m<1
Cực trị
Nhận biết
Câu 3: Số điểm cực tiểu của hàm số là:
A. 2	B. 1	C. 3 	D. 4	 
Vận dụng thấp
Câu 4: Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số là:
A. 2	B.2.	 C.	 	 D.4.
GTLN-GTNN
Thông hiểu
Câu 5. Tìm giá trị nhỏ nhất của hàm số trên đoạn .
 A. 	B. 	 C. 	 D. 
Vận dụng thấp
Câu 6: cho hàm số . số đường tiệm cận của đồ thị hàm số bằng:
A. 3	B. 0	C. 1	D. 2
Tiệm cận
Nhận biết
Câu 7: Số đường tiệm cận của độ thị hàm số là:
A . 2 	B. 1	C. 3	D. 0
Thông hiểu
Câu 8: Giá trị của để đồ thị hàm số không có tiệm cận đứng là
A. . 	B. . 	C. . 	D. . 
ĐỒ THỊ 
Nhận biết
Câu 9: Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
 A. 	B. 	C. D. 
Thông hiểu
Câu 10: Bảng biến thiên ở hình bên dưới là bảng biến thiên của một trong bốn hàm số ở các đáp án A, B, C, D. Hàm số đó là hàm số nao?
x
 - - 
 -1 
 -1 
A..	 B..	C. .	D. 
Vận dụng thấp
Câu 11: Đồ thị hàm số cắt đồ thị hàm số y = x2 -3x +1 tại hai điểm phân biệt A, B. Khi đó độ dài AB bằng bao nhiêu?
A. AB = 1 	B. AB = 3 	C. 	D. 2
ChươngII. Hàm số lũy thừa, hàm số mũ và hàm số logarit.
Lũy thừa
Nhận biết 
Câu 12: Cho biểu thức . Hãy tìm biểu thức K được viết dưới dạng lũy thừa với số mũ hữu tỉ.
 A. 	B. 	C. 	D. 
Thông hiểu 
Câu 13: Câu 17: Mệnh đề nào sau đây đúng: ?
A. 	B. 
C. 	D. 
Hàm số lũy thừa 
Nhận biết
Câu 14: Đạo hàm của hàm số là:
A. 	B. 	C. 	D. 
Lôgarit
Nhận biết
Câu 15: Tìm tất cả các giá trị thực của để biểu thức có nghĩa.
A. 	B. 	C. 	D. 
Thông hiểu
Câu 16: Cho log3 = a; log 2=b.Biểu diễn theo a và b là:
A. 	B. 	C. 	 D. 
Hàm số mũ. Hàm số lôgarit
Nhận biết 
Câu 17: Tính đạo hàm của hàm số: 
A. 	B. 	C. 	D. 
Phtrình mũ và PT lôgarit
Thông hiểu
Câu 18 : Tìm tập nghiệm của phương trình: .
A. 	B. 	C. 	D. 
Vận dụng
Câu 19: Tìm tập nghiệm của phương trình: .
A. 	B. 	C. 	D. 
BPT mũ và BPTlôgarit
Thông hiểu
Câu 20 : Nghiệm của bất phương trình 
A. 2 3 C. x 3
Nguyên hàm
Nhận biết
Câu 21: Tính nguyên hàm của hàm số: 
	A. 	B. 	 	 
	C. 	 	 D. 	
Tích phân
Nhận biết : 
Câu 22: 
A. 	B. 	C. 	D. 
Thông hiểu
Câu 23: Biết tích phân = aln2 + b . Thì giá trị của a là
A. 7	B. 2	C. 3 	D. 1
Câu 24: Tìm khẳng định sai trong các khẳng định sau : 
A. 	B. 	
C. 	D. 
Vận dụng:
Câu 25: Nếu gọi thì khẳng định nào sau đây là đúng?
A. 	B. 
C. 	D. 
Ứng dụng của tích phân trong hình học
Thông hiểu.
Câu 26: Khối tròn xoay tạo nên khi ta quay quanh trục Ox hình phẳng giới hạn bởi đồ thị (P): y = 2x - x2 và trục Ox có thể tích là:
A. 	B. 	C. 	D. 
Câu 27: Hình phẳng giới hạn bởi có diện tích là:
A. 	B. 	C. 	D. 1
Số phức
Nhận biết
Câu 28: Cho i là đơn vị ảo . Số phức 5i có :
A. Phần thực là 0 và phần ảo là 5. 	B. Phần thực là 0 và phần ảo là 5i.
C. Phần thực là 0 và phần ảo là i.	D. Phần thực là 5 và phần ảo là 0.
Thông hiểu
Câu 29: Cho i là đơn vị ảo . Với thì số x -1 + (y + 3)i là số thực khi và chỉ khi : 
A. y = -3 	B. x = 1 	C. 	D. 
Cộng, trừ và nhân , chia số phức
Thông hiểu
Câu 30 : Thu gọn số phức z = ta được: 
A. z =	B. z = 	C. z = 	D. z = 
Ph.trình bậc 2với hệ số thực
Nhận biết
Câu 31 : Tìm số phức z thỏa mãn z2 +4z +13 =0 
A. 	B. 	C. 	D. 
Chương I: Khối đa diện
Nhận biết 
Câu 32: Hình lập phương có bao nhiêu mặt phẳng đối xứng.
A. 9. 	B. 4.	C. 7 	D. 8 
Câu 33: Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau:
A. Mỗi cạnh là cạnh chung của ít nhất ba mặt . B. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh . 
C. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt D. Mỗi mặt có ít nhất ba cạnh
Câu 34: Khối 12 mặt đều thuộc loại: 
A. 	B. 	C. 	D. 
Thông hiểu 
Câu 35: Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a . Thể tích của (H) bằng:
A. 	B. 	C. 	D. 
Câu 36: Cho hình lăng trụ đứng ABC.A’B’C’ có tất cả các cạnh đều bằng a . Thể tích khối tứ diện A’BB’C bằng: 
A. 	B. 	C. 	D. 
Câu 37: Cho hình chóp S. ABCD đáy là hình vuông cạnh a, SA vuông góc với đáy và góc giữa mp(SBD) và đáy bằng 600. Đường cao của khối chóp là :
A. 	B. 	C. 	D. 
Vận dụng 
Câu 38: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của A’ xuống mp(ABC) là trung đểm của AB. Mặt bên (AA”C”C) tạo với đáy một góc bằng 450 . Thể tích khối lăng trụ ABC.A’B’C’ bằng :
A. 	B. 	C. 	D. 
Chương II. Mặt nón, mặt trụ, mặt cầu
Nhận biết 
Câu 39: Cho ba điểm A,B,C nằm trên một mặt cầu , biết rằng góc . Trong các khẳng định sau, khẳng định nào đúng ?
A. Luôn có một đường tròn nằm trên mặt cầu ngoại tiếp tam giác ABC 
B. AB là một đường kính của mặt cầu 
C. Tam giác ABC vuông cân tại C
D. Mặt phẳng (ABC) cắt mặt cầu theo giao tuyến là một đường tròn lớn
Câu 40: Cho hình nón có bán kính đáy là 3a, chiều cao là 4a. thể tích của hình nón là:
A. 	B. 	C.	D. 
Thông hiểu 
Câu 41: Cho hình chóp S.ABCD có thể tích bằng 48, đáy ABCD hình thoi. Các điểm M, N, P, Q lần lượt thuộc S, SB, SC, SD thỏa mãn SA = 2 SM; SB = 3 SN, SC = 4SP , SD = 5 SQ. Thể tích khối chóp S.MNPQ .
A. 	B. 	C. 	D. 
Chương III. Phương pháp tọa độ trong không gian
Nhận biết 
Câu 42: Trong không gian với hệ tọa độ . Cho vectơ , khi đó độ dài của bằng:
 A. 3 B. 4 C. 5 D. 
Câu 43: Trong không gian với hệ tọa độ . Mp(P) : 2x – y + 5 = 0 , vec tơ pháp tuyến của mp(P) là:
A. ( 2; -1; 0) 	B. ( 2; 0; -1) 	C. ( 2; -1 ; 5) 	D. ( 2; -1 ; 1)
Câu 44: Trong không gian với hệ tọa độ , cho đường thẳng d đi qua điểm và có vectơ chỉ phương . Phương trình tham số của đường thẳng d là:
A. B. C. D. 
Câu 45: Trong không gian với hệ tọa độ , cho điểm . Phương trình đường thẳng d đi qua A, B là: 
 A. B. C. D. 
Thông hiểu
Câu 46: Trong không gian với hệ tọa độ , cho các điểm A(1;-1;1), B(1;3;1), C(4;3;1) . Tìm tọa độ đỉnh 
D sao cho các điểm A, B, C, D là các đỉnh của hình chữ nhật:
 A. B. C. D. 
Câu 47: Trong không gian với hệ tọa độ , cho các điểm A(3;2;1), B(1;0;3). Phương trình mặt phẳng trung
trực của đoạn thẳng AB là: 
A. 	 B. 	
C. 	 D. 
Câu 48: Trong không gian với hệ trục tọa độ Oxyz, đường thẳng d qua điểm A(1; 2; 3) và vuông góc với mp(P) :2x + 2 y + z + 2017 = 0 có phương trình là:
A. 	B. 
C. 	D. 
Vận dụng
Câu 49 : Gọi (S) là mặt cầu tâm I(2; 1; -1) tiếp xúc (P) : 2x – 2y – z +3 = 0 . Bán kính mặt cầu (S) bằng :
A. 2	B. 	C. 	D. 
Câu 50: Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng . Viết phương trình đường thẳng đi qua điểm A, vuông góc với đường thẳng d và cắt trục Ox.
A. 	B. 
C. 	D. 
HẾT