Đề ôn tập môn Toán - Đề 19

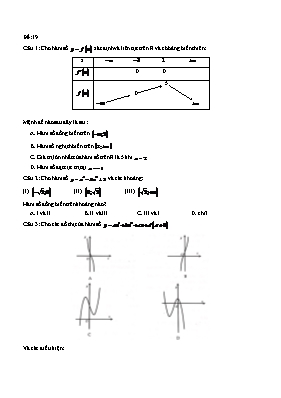
Đề:19
Câu 1: Cho hàm số xác định và liên tục trên R và có bảng biến thiên:
x
 2 
0 0
 5
 0
Mệnh đề nào sau đây là sai:
	A. Hàm số đồng biến trên 
	B. Hàm số nghịch biến trên 
	C. Giá trị lớn nhất của hàm số trên R là 5 khi 
	D. Hàm số đạt cực trị tại 
Câu 2: Cho hàm số và các khoảng:
(I) 	(II) 	(III) 
Hàm số đồng biến trên khoảng nào ?
	A. I và II	B. II và III	C. III và I	D. chỉ I
Câu 3: Cho các đồ thị của hàm số 
.
Và các điều kiện:
1. 	2. 
3. 	4. 
Hãy chọn sự tương ứng đúng giữa các dạng đồ thị và điều kiện:
	A. 	B. 
	C. 	D. 
Câu 4: Tìm lỗi sai trong bài toán khảo sát hàm số của một bạn học sinh như sau:
Bài giải
1. Tập xác định: 
2. Sự biến thiên:
+) Chiều biến thiên 
y' không xác định khi ; y' luôn âm với mọi 
vậy hàm số nghịch biến trên và 
+) Cực trị: Hàm số đã cho không có cực trị
+) Tiệm cận:
Do đó đường thẳng là tiệm cận đứng
Vậy đường thẳng là tiệm cận ngang
+) Bảng biến thiên:
x
y'
y
	A. Bài giải trên sai ở giai đoạn tìm điều kiện xác định
	B. Bài giải trên đạo hàm sai
	C. Bài giải trên sai ở giai đoạn tìm tiệm cận
	D. Bài giải trên sai bảng biến thiên
Câu 5: Cho hàm số . Kết luận nào sau đây là đúng ?
	A. 	B. 	C. 	D. 
Câu 6: Giao điểm có hoành độ là số nguyên của đồ thị hàm số và đồ thị hàm số là:
	A. 	B. 	C. 	D. 
Câu 7: Gọi m là số điểm cực trị của đồ thị hàm số 
	n là số điểm cực trị của đồ thị hàm số 
	p là số điểm cực trị của đồ thị hàm số 
Kết luận nào sau đây là sai ?
	A. 	B. 	C. 	D. 
Câu 8: Gọi A, B là hai điểm cực trị của đồ thị hàm số . Khẳng định nào sau đây là đúng ?
	A. Trung điểm của đoạn AB nằm trên đường thẳng 
	B. Đường thẳng AB vuông góc với đường thẳng 
	C. A, B và thẳng hàng.
	D. Diện tích tam giác ABC bằng 12 với 	
Câu 9: Đồ thị hàm số có
	A. Đường tiệm cận đứng và không có tiệm cận ngang
	B. Đường tiệm cận ngang và không có tiệm cận đứng.
	C. Đường tiệm cận đứng và tiệm cận ngang 
	D. Có hai đường tiệm cận đứng và 
Câu 10: Tìm m để đồ thị hàm số có đúng một tiệm cận ngang
	A. 	B. 
	C. 	D. 
Câu 11: Khi sản xuất hộp mì tôm, các nhà sản xuất luôn để một khoảng trống ở dưới đáy hộp để nước chảy xuống dưới và ngấm vào vắt mì, giúp mì chín. Hình vẽ dưới mô tả cấu trúc của một hộp mình tôm (hình vẽ chỉ mang tính chất minh họa). Vắt mì tôm có hình một khối trụ, hộp mì tôm có dạng hình nón cụt được cắt ra bởi hình nón có chiều cao 9cm và bán kính đáy 6cm. Nhà sản xuất đang tìm cách để sao cho vắt mì tôm có thể tích lớn nhất trong hộp với mục địch thu hút khách hàng. Tìm thể tích lớn nhất đó ?
	A. 	B. 	C. 	D. 
Câu 12: Giải bất phương trình ?
	A. 	B. 	C. 	D. 
Câu 13: Tìm tập xác định của hàm số 
	A. 	B. 	C. 	D. 
Câu 14: Tính đạo hàm của hàm số 
	A. 	B. 	C. 	D. 
Câu 15: Gọi và . Bất đẳng thức nào sau đây đúng ?
	A. 	B. 	C. 	D. 
Câu 16: Biểu thức 
	A. 	B. 	C. 	D. 2
Câu 17: Bất phương trình tương đương với mệnh đề nào sau đây ?
	A. với 	B. với 
	C. 	D. hay 
Câu 18: Tổng hai nghiệm của phương trình 
	A. 5	B. 6	C. 4	D. 7
Câu 19: Tìm khẳng định sai trong các khẳng định sau:
	A. 	B. 
	C. 	D. 
Câu 20: Đạo hàm của hàm số có dạng:
	A. 	B. 	C. 	D. 
Câu 21: Số tiền 58 000 000đ gửi tiết kiệm trong 9 tháng thì lãnh về được 61758000đ. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu ?
	A. 0,8%	B. 0,7%	C. 0,5%	D. 0,6%
Câu 22: Mệnh đề nào sai trong các mệnh đề sau:
	A. Nếu F(x) là một nguyên hàm của hàm số trên K thì với mỗi hằng số C, hàm số cũng là một nguyên hàm của hàm số trên K.
	B. Mọi hàm số liên tục trên K đều có nguyên hàm trên K.
	C. Với mỗi hàm số xác định trên K, hàm số được gọi là nguyên hàm của hàm số trên K khi .
	D. Nếu và là hàm số có đạo hàm liên tục thì 
Câu 23: Tìm nguyên hàm của hàm số 
	A. 	B. 
	C. 	D. 
Câu 24: Tính thể tích của khối tròn xoay được tạo thành khi quay hình phẳng được giới hạn bởi quanh trục Ox.
	A. 	B. 	C. 	D. 
Câu 25: Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích không bằng nhau:
	A. và 
	B. và 
	C. và 
	D. với và với 
Câu 26: Diện tích hình phẳng giới hạn bởi đồ thị hàm số ; tiệm cận ngang và hai đường thẳng được tính bằng:
	A. 	B. 	C. 	D. 
Câu 27: Một vật chuyển động chậm dần với vận tốc . Hỏi rằng trong 3s trước khi dừng hẳn vật di chuyển được bao nhiêu mét?
	A. 16 m	B. 130 m	C. 170 m	D. 45 m
Câu 28: Tính tích phân 
	A. 	B. 	C. 	D. 
Câu 29: Cho . Trong các mệnh đề sau mệnh đề nào sai ?
	A. 
	B. 
	C. 
	D. 
Câu 30: Tính 
	A. 	B. 	C. 	D. 
Câu 31: Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức sao cho là số thuần ảo.
	A. Trục tung, bỏ điểm 	B. Trục hoành, bỏ điểm 
	C. Đường thẳng , bỏ điểm 	D. Đường thẳng , bỏ điểm 
Câu 32: Số phức z thỏa mãn: . Mô đun của z là :
	A. 	B. 	C. 	D. 
Câu 33: Gọi A là điểm biểu diễn của số phức và điểm B là điểm biểu diễn số phức . Tìm mệnh đề đúng trong các mệnh đề sau:
	A. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O.
	B. Hai điểm A và B đối xứng với nhau qua trục tung.
	C. Hai điểm A và B đối xứng nhau qua trục hoành
	D. Hai điểm A và B đối xứng nhau qua đường thẳng 
Câu 34: Tìm tất cả các nghiệm của , biết là một nghiệm của phương trình:
	A. 	B. 
	C. 	D. 
Câu 35: Cho hình chóp đều S.ABC. Người ta tăng cạnh đáy lên 2 lần. Để thể tích giữ nguyên thì tan góc giữa cạnh bên và mặt phẳng đáy giảm bao nhiêu lần để thể tích giữ nguyên?
	A. 8	B. 2	C. 3	D. 4
Câu 36: Bé Bách có một tấm bìa có chiều dài 20cm, chiều rộng 1cm. Bé muốn gấp một cái hộp nhỏ xinh để bỏ kẹp tóc vào hộp đó tặng quà cho mẹ ngày 20 tháng 10. Anh Siêu đã chỉ cho bé hai cách gấp hộp. Cách thứ nhất là bé cuốn tấm bìa thành một cái hộp hình trụ không có 2 đáy có thể tích V1.
Cách thứ hai là bé gập tấm bìa một hình hộp chữ nhật có thể tích V2 có các kích thước như hình vẽ. Hãy tìm tỉ số thể tích của 2 hộp để biết được gấp theo cách nào sẽ có thể tích lớn hơn
	A. 	B. 	C. 	D. 
Câu 37: Cho hình hộp chữ nhật có ba kích thước a, b, c thì đường chéo d có độ dài là:
	A. 	B. 
	C. 	D. 
Câu 38: Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh 2a, có SA vuông góc với (ABC), tam giác SBC cân tại S. Để thể tích của khối chóp S.ABC là thì góc giữa hai mặt phẳng (SBC) và (ABC) là:
	A. 	B. 	C. 	D. Đáp án khác.
Câu 39: Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và . Kẻ AH vuông góc với SB và AK vuông góc với SD. Mặt phẳng (AHK) cắt SC tại E. Tính thể tích khối cầu ngoại tiếp khối ABCDEHK.
	A. 	B. 	C. 	D. 
Câu 40: Mặt cầu tâm O bán kính . Mặt phẳng (P) cắt mặt cầu sao cho giao tuyến đi qua ba điểm A, B, C mà . Tính khoảng cách từ O đến (P).
	A. 7 dm	B. 8 dm	C. 14 dm	D. 16 dm
Câu 41: Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh góc vuông bằng . Tính thể tích của khối nón
	A. 	B. 	C. 	D. 
Câu 42: Cho hình trụ có bán kính đáy là , mặt phẳng qua trục và cắt hình trụ theo một thiết diện có diện tích bằng . Diện tích xung quanh của hình trụ và thể tích của khối trụ là
	A. 	B. 	C. 	D. 
Câu 43: Cho . Tìm tọa độ điểm đối xứng của M qua mặt phẳng Oxy.
	A. 	B. 	C. 	D. 
Câu 44: Viết phương trình mặt phẳng qua và song song với trục Ox.
	A. 	B. 
	C. 	D. 
Câu 45: Tính thể tích tứ diện OABC biết A, B, C lần lượt là giao điểm của mặt phẳng với trục Ox, Oy, Oz.
	A. 78	B. 120	C. 91	D. 150
Câu 46: Tìm m để phương trình 
Là phương trình một mặt cầu ?
	A. 	B. 	C. 	D. 
Câu 47: Cho đường thẳng , mặt phẳng và điểm . Đường thẳng qua A cắt d và song song với mặt phẳng (P) có phương trình:
	A. 	B. 
	C. 	D. 
Câu 48: Xác định m để đường thẳng cắt mặt phẳng .
	A. 	B. 	C. 	D. 
Câu 49: Lập phương trình mặt cầu có tâm nằm trên đường thẳng và tiếp xúc với hai mặt phẳng: 
	A. 
	B. 
	C. 
	D. 
Câu 50: Trong không gian với hệ tọa độ Oxyz cho đường thẳng và mặt phẳng . Để đường thẳng d vuông góc với (P) thì:
	A. 	B. 	C. 	D. 
Đáp án
1-D
6-A
11-C
16-D
21-B
26-B
31-A
36-A
41-B
46-B
2-C
7-B
12-B
17-C
22-C
27-D
32-C
37-A
42-D
47-B
3-A
8-A
13-B
18-B
23-B
28-A
33-D
38-D
43-C
48-B
4-C
9-C
14-A
19-C
24-A
29-D
34-C
39-A
44-D
49-A
5-B
10-D
15-A
20-A
25-B
30-B
35-A
40-B
45-D
50-A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Đáp án D
Phân tích: Đây là bài toán tìm lỗi sai, nên quý độc giả sẽ phải đi xem xét từng mệnh đề một:
- Nhìn vào BBT ta thấy mệnh đề A và B đúng. Ở phần giá trị của trong BBT ta nhận thấy GTLN của là 5 trên R. Vậy theo quy tắc loại trừ ta sẽ chọn đáp án D. Tuy nhiên, ở đây tôi vẫn chỉ ra cho quý độc giả thấy vì sao ý D lại sai.
Cùng nhắc lại các kiến thức về cực trị mà chúng ta đã được học trên lớp thông qua cuống SGK Giải tích 12 cơ bản trang 14.
"Giả sử hàm số liên tục trên khoảng và có đạo hàm trên K hoặc trên , với .
A, Nếu trên khoảng và trên khoảng thì là một điểm cực đại của hàm số 
b, Nếu trên khoảng và trên khoảng thì là một điểm cực tiểu của hàm số ."
Khi nhìn vào BBT ta nhận thấy, hai khoảng trước và sau điểm đều có giá trị dương, vậy rõ ràng tại , hàm số không có đạt cực trị.
Câu 2: Đáp án C
Phân tích: Khi gặp các bài toán dạng này hãy tính đạo hàm thật nhanh.
Hãy nhớ đến bảng các dạng đồ thị của hàm số bậc bốn trong sách giáo khoa (trang 38) mà nhiều lần tôi đã nhắc đến cho quý độc giả, dĩ nhiên quý độc giả có thể làm theo cách khác.
Tuy nhiên chúng ta đang luyện tập, vì thế khi đọc lời giải cũng là lúc rèn luyện thêm khả năng tư duy.
Nhân thấy đây là hàm bậc bốn trùng phương có , phương trình có ba nghiệm phân biệt. Vậy đồ thị hàm số sẽ có hình chữ W đối xứng (đây là cách nhớ mẹo thôi). Nghĩa là đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu. Dĩ nhiên sẽ cực đại tại , và cực tiểu tại . Theo hình chữ W thì ta thấy hàm số sẽ đồng biến trên và . Cách nháp mẹo như sau:
+) Sau khi đã suy ra được đồ thị hàm số hình chữ W, quý độc giả có thể nháp:
Ta luôn điền điểm 0 vào vị trí trung tâm, 2 điểm còn lại điền 2 bên
Nhìn vào các đường lên xuống của chữ W, lúc này quý độc giả có thể dễ dàng định dạng được khoảng đồng biến nghịch biến như tôi đã xác định ở trên.
Với bài toán khác dạng đồ thị ví dụ như chữ M (trường hợp với có ba nghiệm phân biệt). Sẽ nhanh thôi, vẽ một đường W sẽ nhanh hơn rất nhiều so với việc các bạn ngồi bấm máy tính thử, hay vẽ bảng biến thiên rồi bấm xem lớn hơn hay nhỏ hơn 0. Các quý độc giả có thể tự đặt ra quy tắc nhớ dạng đồ thị cho mình, rồi từ đso đưa ra các kinh nghiệm.
Câu 3: Đáp án A
Phân tích: Lại một bài toán đòi hỏi quý độc giả nhớ dạng đồ thị, nhưng ở bài này là hàm số bậc ba.
Ở hàm số bậc ba hãy nắm rõ quy tắc này: hàm số bậc ba không có cực trị khi phương trình vô nghiệm hoặc có nghiệm kép. Nguyên lý rõ ràng của câu trên quý độc giả đã học ở chương trình SGK nên tôi không nhắc lại ở đây. Hoặc quý độc giả có thể nhớ câu, hàm số bậc ba có cực trị khi phương trình có hai nghiệm phân biệt. TH không có cực trị là TH còn lại của phương trình , tức là vô nghiệm hay nghiệm kép.
Khi đó ta có thể dễ dàng xác định được đồ thị A và B là ở TH phương trình VN hay nghiệm kép.
. Và đồ thị C, D là TH còn lại
Xét phương trình ;
 (chính là biểu thức được nhắc đến trong các điều kiện trong đề bài).
Vậy với đồ thị A và B sẽ được ghép với các điều kiện có , tức là 2 hoặc 4.
Tiếp tục xét đến a, như trong bảng với thì hàm số luôn luôn đồng biến và thì hàm số luôn nghịch biến. (quý độc giả có thể xem lại phần giải bất phương trình đã học ở lớp dưới, dấu của tam thức bậc hia có denta nhỏ hơn không phụ thuộc vào hệ số a.)
Vậy: đến đây ta có thể chọn đáp án A luôn, nhưng hãy xem xét cả phần các đồ thị còn lại, vì quý độc giả đang trong quá trình ôn luyện.
Câu 4: Đáp án C
Phân tích: Bài toán trên đã làm lần lượt ở các bước rất đầy đủ. Có thể nếu soát không kĩ lưỡng, quý độc giả sẽ nghĩ câu này không có đáp án. Tuy nhiên, khi đi xét từng bước một ta thấy, phần xét tiệm cận, cụ thể hơn là tìm tiệm cận đứng, bạn đã giải sai tìm lim, cụ thể như sau:
. Sửa thành 
Câu 5: Đáp án B
Phân tích: Nếu đã nhớ kĩ rồi thì quý độc giả có thể mường tượng trong đầu. Để ý kĩ nhé, với bài này có thể quý độc giả sẽ không cần viết biểu thức ra nữa mà vẫn có thể tìm được đáp án. Vì sao ?
Phương trình tổng quát sẽ là
, vậy phương trình có 3 nghiệm phân biệt khi , nghĩa là a và b trái dấu. Ở đây rõ là a và b trái dấu. Như ở câu 2 tôi đã phân tích về dạng đồ thị hàm trùng phương bậc bốn, với có 3 nghiệm phân biệt thì đồ thị dạng W tức là hàm số sẽ đạt cực đại tại . Khi đó 
Câu 6: Đáp án A
Phân tích: ta xét phương trình hoành độ giao điểm: 
 chọn giá trị này vì điều kiện x là số nguyên.
Câu 7: Đáp án B
Phân tích: Bài toán này củng cố cho quý độc giả về cách tìm nhanh số cực trị của hàm số bậc ba. Ta sẽ lần lượt đi xét phương trình của mỗi hàm số.
 phương trình có nghiệm kép nghĩa là đồ thị hàm số không có điểm cực trị nào 
. Bấm máy tính thấy phương trình vô nghiệm 
 bấm máy tính thấy phương trình có 2 nghiệm phân biệt .
Đến đây ta có thể nhận ra đáp án 
Câu 8: Đáp án A
Phân tích: Ta đi tìm hai điểm cực trị của hàm số, do ở đây không bắt xác định điểm cực đại, cực tiểu nên ta đi tìm hai điểm cực trị àm không cần xác định cực đại, cực tiểu.
Giả sử 
Đường thẳng qua A, B:
 (lúc này quý độc giả có thể bấm máy tính như lúc học cấp hai, tìm đường thẳng đi qua hai điểm biết tọa độ cho trước, sẽ rất nhanh). Khi đó với phương án C, thay tọa độ điểm D vào phương trình không thỏa mãn, vậy loại đáp án này. Cũng với dữ kiện này ta loại được luôn ý C.
Với đáp án A ta tìm được tọa độ trung điểm AB là nằm trên đường thẳng ở ý A, vậy ta chọn A mà không cần xét đến D nữa.
Câu 9: Đáp án C
Phân tích: Như ở các đề trước tôi đã đề cập đến cách nhẩm tìm tiệm cận đứng, ngang của đồ thị hàm số phân thức bậc nhất trên bậc nhất. Ta sẽ nhẩm được là TCĐ, là TCN. Và chọn luôn đáp án C mà không cần xét đến các phương án khác.
Câu 10: Đáp án D
Phân tích: Nhận thấy 
Tương tự: 
Vậy đồ thị hàm số luôn có một tiệm cận ngang y = 1.
Vậy với mọi m mà hàm số đã cho xác định, ta luôn có một tiệm cận ngang, tức là ta đi tìm điều kiện xác định của hàm số: .
Phương trình VN khi 
Câu 11: Đáp án C
Phân tích: Đây thực chất là bài toán khối trụ nội tiếp khối nón, ta có kí hiệu các kích thước như sau:
Ta có thể tích vắt mì tôm được tính bằng 
Đây là ứng dụng của bài toán tìm GTLN, GTNN trên một khoảng (đoạn) xác định:
Ta sẽ đưa thể tích về hàm số một biến theo h hoặc r. Trước tiên ta cần đi tìm mối liên hệ giữa h và r. Nhìn vào hình vẽ ta thấy các mối quan hệ vuông góc và song song, dùng định lí Thales ta sẽ có: 
Khi đó với 
Khi đó ta không cần phải vẽ BBT ta cũng có thể suy ra được với thì V đạt GTLN, khi đó 
Câu 12: Đáp án B
Phân tích: Điều kiện 
Phương trình 
. Kết hợp với điều kiện xác định thì ta chọn đáp án B.
Câu 13: Đáp án B
Phân tích: Ở đây có hai điều kiện để cho biểu thức xác định, một số độc giả chỉ làm điều kiện để căn tồn tại mà quên điều kiện xác định của logarit:
Điều kiện:
Đáp án B
Câu 14: Đáp án A
Phân tích: ta có công thức tổng quát của cách tính đạo hàm hàm logarit.
Khi đó áp dụng công thức vào ta được
Đây là bài toán đơn giản gỡ điểm nên hãy nhớ công thức đạo hàm nhé!
Câu 15: Đáp án A
Phân tích: Đây thực chất là bài toán so sánh hai số mũ, rèn luyện cho quý độc giả các kiến thức về số mũ.
Hai số M và N có cùng cơ số là 3>1 nên ta chỉ cần so sánh hai số mũ, tức là so sánh và .
Tôi xin nhắc lại kiến thức so sánh hai logarit như sau:
Với và 
- Nếu thì 
	 thì 
- Nếu thì 
	 thì 
Áp dụng vào bài toán ta thấy cơ số của hai logarit nằm trong khoảng nên
Từ đó suy ra . Đáp án A
Một cách làm nhanh là bạn có thể xét hiệu của M và N trên máy tính và từ đó suy ra đáp án, tuy nhiên đây là quá trình ôn luyện nên tôi vẫn mong quý độc giả có thể nhớ công thức bằng việc suy luận như tôi đã nêu ở trên.
Câu 16: Đáp án D
Phân tích: Cũng giống như câu 15, quý độc giả có thể bấm máy tính tìm được đáp án, tuy nhiên ở đây tôi giới thiệu cho quý độc giả cách suy luận thông thường. Có thể với bài toán này ra kết quả chẵn sẽ dễ dàng tìm ra. Nhưng vì là trong quá trình rèn luyện, hãy rèn luyện tư duy của mình thật tốt nhé!
Câu 17: Đáp án C
Phân tích: Đặt . Khi đó bất phương trình trở thành:
Đến đây ta có thể loại đáp án A và B
Với đáp án C và D là kết quả của x vì thế ta cần đi giải nghiệm của bất phương trình
(đáp án C)
Câu 18: Đáp án B
Phân tích: bài toán lại đòi hỏi quý độc giả phải giải bài toán ra, chứ không thử nghiệm được. Ta không cần tìm điều kiện vì để ý kĩ ở đây nếu giải ra phương trình cuối của chúng ta sẽ là phương trình bậc hai, áp dụng viet là ta sẽ có tổng hai nghiệm của phương trình ngay.
Phương trình 
Tổng hai nghiệm của phương trình 
. Đáp án B
Có thể quý độc giả không cần viết rõ phương trình cuối ra vì rõ ràng hệ số của x và sẽ không thay đổi, không ảnh hưởng đến việc áp dụng Viet. Nên hãy để ý kĩ, xử lý linh hoạt trong từng tình huống để làm bài nhanh nhất.
Câu 19: Đáp án C
Phân tích: Dạng đề xác định tính đúng sai của mệnh đề, do đó ta cần đi xem xét từng mệnh đề một.
Với mệnh đề A: đây là mệnh đề đúng do nên 
Với mệnh đề B: cũng tương tự, do ta ra và kết hợp với điều kiện để logarit tồn tại thì ta sẽ được 
Với mệnh đề C: nếu đã đọc kĩ phần lời giải của tôi ở câu 15 thì chắc hẳn quý độc giả sẽ giải suy ra luôn được đây là mệnh đề sai, do .
Ta không cần xét đến đáp án D nữa
Câu 20: Đáp án A
Phân tích: Ta có công thức tính đạo hàm như sau:
 và công thức tính đạo hàm của logarit tôi đã nêu ở câu 14 ta sẽ giải được như sau:
Hãy rèn luyện thật nhiều để tạo thêm động lực làm các bài thật nhanh nhé!
Câu 21: Đáp án B
Phân tích: Bài toán lãi suất ngân hàng dựa trên kiến thức về số mũ ở chương trình lớp 12.
Ta có gọi mức lãi suất hàng tháng là a%
Sau tháng thứ nhất số tiền trong tài khoản của người đó là: 
Sau tháng thứ hai số tiền trong tài khoản của người đó là: 
Sau tháng thứ chín số tiền trong tài khoản của người đó là: 
Câu 22: Đáp án C
Phân tích: Ta lần lượt đi xét từng mệnh đề một.
Với mệnh đề A: Đây là mệnh đề đúng, vì ta đã học công thức tính nguyên hàm và có là cộng thêm hằng số C. Mỗi biểu thức với C khác nhau sẽ là một nguyên hàm của hàm số đã cho.
Với mệnh đề B: Đây là mệnh đề đúng, với hàm số liên tục trên K thì sẽ có nguyên hàm trên K.
Với mệnh đề C: Ta nhận thấy khi . Hãy nhớ rằng số nguyên hàm chính là ngược lại của đạo hàm (đây là cách nhớ nôm na thôi bạn nhé). Vậy C chính là mệnh đề sai. Ta chọn luôn đáp án C.
Quý độc giả đang trong quá trình ôn luyện nên hãy tham khảo cả các mệnh đề đúng, để khắc sâu kiến thức nhé!
Câu 23: Đáp án B
Phân tích: Đây không phải là bài toán tính tích phân, do đó quý độc giả không thể dùng máy tính để bấm được mà phải tìm ra công thức cụ thể. Hoặc quý độc giả có thể bấm máy tính, tuy nhiên cách làm duy nhất có lẽ là thêm cận vào và thử từng đáp án một.
Câu 24: Đáp án A
Phân tích: Để tính được thể tích của khối tròn xoay dựa trên ứng dụng của tích phân ta cần đi tìm hai cận a, b bằng việc tìm nghiệm của phương trình hoành độ giao điểm:
Ta có thể tính thể tích của khối tròn xoay giới hạn bởi được tính bằng công thức 
Đến đây ta có thể làm theo hai cách:
Cách 1: Bấm máy tính
Chọn nút trên máy tính và nhập vào biểu thức tính tích phân vào.
Chú ý trên máy tính CASIO fx-570VN PLUS thì giá trị tuyệt đối chính là nút Abs (Absolute), chính là kí hiệu màu vàng ở bên nút Hyperbol được bấm bằng cách ấn nút SHIFT + Hyperbol sau khi nhập vào máy tính sẽ hiện kết quả như sau:
Vậy kết quả của chúng ta là đvtt
Cách 2: Giải tích về mặt toán học:
Để bỏ được dấu trị tuyệt đối trong tích phân, ta cần xét khoảng rồi áp dụng công thức sau trong tích phân:
Nhận thấy: tuy nhiên ở đây, hàm số luôn lớn hơn 0 với mọi 
Khi đó 
Câu 25: Đáp án B
Phân tích: Đối với bài toán này ta không còn cách nào khác là đi xét từng đáp án một, vì bài toán có tận bốn phương án, do đó trường hợp xấu nhất là quý độc giả phải đi kiểm tra ba đáp án, tức là tính ba tích phân. Do đó, lựa chọn tối ưu chính là sử dụng máy tính để tối ưu thời gian.
Với phương án A: Ta có thể nhẩm nhanh được cận của hai công thức tính diện tích hình phẳng. Khi đó bấm máy tính như ở Câu 24 tôi đã giới thiệu cho quý độc giả thì sẽ ra được kết quả. Hãy bấm hiệu của hai tích phân, nếu bằng 0 thì ta sẽ loại đáp án đó ra và tiếp tục xét.
Ta nhập công thức sau vào máy tính:
Sau