Đề kiểm tra Toán 8 - Học kì I năm học 2010 - 2011 - Trường THCS Nam Hà

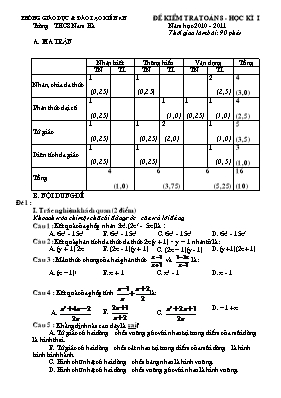
Nhận biết
Thông hiểu
Vận dụng
Tổng
TN
TL
TN
TL
TN
TL
Nhân, chia đa thức
1
 (0,25)
1
 (0,2 5)
2
 (2,5)
4
(3,0)
Phân thức đại số
1
 (0,25)
1
 (1,0)
1
 (0,25)
1
 (1,0)
4
(2,5)
Tứ giác
1
 (0,25)
1
 (0,25)
2
 (2,0)
1
 (1,0)
5
(3,5)
Diện tích đa giác
1
 (0,25)
1
 (0,25)
1
 (0, 5)
3
(1,0)
Tổng
4
 (1,0)
6
 (3,75)
6
 (5,25)
16
(10)
Phòng Giáo Dục & Đào tạo Kiến An Đề kiểm tra toán 8 - Học kì I
Trường THCS Nam Hà Năm học 2010 - 2011 
 Thời gian làm bài: 90 phút 
A. Ma trận
B. Nội dung đề
Đề 1: 
I. Trắc nghiệm khách quan (2 điểm)
Khoanh tròn chỉ một chữ cái đứng trước câu trả lời đúng
Câu 1: Kết quả của phép nhân 3x2.(2x3 - 5x) là : 
A. 6x5 - 15x2 
B. 6x5 - 15x2 
C. 6x5 - 15x2 
D. 6x5 - 15x3
Câu 2: Kết quả phân tích đa thức đa thức 2x(y + 1) - y – 1 nhân tử là :
A. (y + 1) 2x
B. (2x - 1)(y + 1) 
C. (2x – 1)(y - 1) 
D. (y+1)(2x + 1)
Câu 3 : Mẫu thức chung của hai phân thức và là : 
A. (x – 1)2
B. x + 1 
C. x2 - 1
D. x - 1
Câu 4 : Kết quả của phép tính là:
 A. 
B. 
C. 
D. – 1 + x
Câu 5 : Khẳng định nào sau đây là sai ?
Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.
B. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình bình hành.
C. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.
D. Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
 A B
D M C
Hình 1
Câu 6: Cho hình vẽ 1, biết ABCD là hình thang vuông, BCM là tam giác đều. Số đo bằng:  
A. 900
B. 1200
C. 1000 
D. 1500
A 5cm D
 4cm
B E C
Hình 2
Câu 7: Cho hình vẽ 2. Diện tích của hình thang ABCD là: 
A. 56cm2
B. 28cm2
C. 36cm2
D. Một kết quả khác
Câu 8: Cho DABC có diện tích là 30cm2; độ dài đường cao ứng với đỉnh A là 6cm. Cạnh đối diện với đỉnh A là:
A. 5cm
B. 10cm 
C. 24 cm 
D. cm 
II. Tự luận (8 điểm)
Câu 9 (2,5 điểm)
Phân tích các đa thức sau thành nhân tử
a) 5x2 - 5xy + 7y - 7x	
b) x2 - y2 + 2x + 1
Câu 10  (2 điểm):
Cho phân thức :
a) Rút gọn A
b) Tính giá trị của A tại x = 2010.
Câu 11 (3,5 điểm): Cho DABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của của GC.
Chứng minh rằng tứ giác DEHK là hình bình hành.
Nếu BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì?
DABC có điều kiện gì thì DEHK là hình chữ nhật? Vẽ hình minh hoạ. 
Khi đó tính diện tích hình chữ nhật DEHK biết BC = 6cm, AG = 4cm.
Đề 2: 
I. Trắc nghiệm khách quan (2 điểm)
Khoanh tròn chỉ một chữ cái đứng trước câu trả lời đúng
Câu 1: Kết quả phân tích đa thức đa thức 2x(y + 1) - y – 1 nhân tử là :
A. (y + 1) 2x
B. (2x - 1)(y - 1) 
C. (2x – 1)(y + 1) 
D. (y+1)(2x + 1)
Câu 2 : Mẫu thức chung của hai phân thức và là : 
A. (x – 1)2
B. x2 - 1 
C. x + 1
D. x - 1
Câu 3: Kết quả của phép nhân 3x2.(2x3 - 5x) là : 
A. 6x5 - 15x2 
B. 6x5 - 15x2 
C. 6x5 - 15x2 
D. 6x5 - 15x3
Câu 4 : Kết quả của phép tính là:
 A. 
B. 
C. 
D. – 1 + x
 A B
D M C
Hình 1
Câu 5: Cho hình vẽ 1, biết ABCD là hình thang vuông, BCM là tam giác đều. Số đo bằng:  
A. 900
B. 1500
C. 1000 
D. 1200
Câu 6 : Khẳng định nào sau đây là sai ?
Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.
B. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình bình hành.
C. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.
D. Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
Câu 7: Cho DABC có diện tích là 30cm2; độ dài đường cao ứng với đỉnh A là 6cm. Cạnh đối diện với đỉnh A là:
A. 5cm
B. 10cm 
C. 24 cm 
D. cm 
A 5cm D
 4cm
B E C
Hình 2
Câu 8: Cho hình vẽ 2. Diện tích của hình thang ABCD là: 
A. 28cm2
B. 36cm2
C. 56cm2
D. Một kết quả khác
II. Tự luận (8 điểm)
Câu 9 (2,5 điểm)
Phân tích các đa thức sau thành nhân tử
a) 5x2 - 5xy + 7y - 7x	
b) x2 - y2 + 2x + 1
Câu 10  (2 điểm): 
Cho phân thức :
a) Rút gọn A
b) Tính giá trị của A tại x = 2010.
Câu 11 (3,5 điểm): Cho DABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của của GC.
Chứng minh rằng tứ giác DEHK là hình bình hành.
Nếu BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì?
DABC có điều kiện gì thì DEHK là hình chữ nhật? Vẽ hình minh hoạ. 
Khi đó tính diện tích hình chữ nhật DEHK biết BC = 6cm, AG = 4cm.
C. Đáp án và biểu điểm
Đề 1:
Phần I:
Trắc nghiệm
(2,0 đ)
Nội dung
Điểm
Câu
1
2
3
4
5
6
7
8
Mỗi câu 0,25 điểm
Đáp án
D
B
C
A
C
C
B
B
Phần I:
Tự luận
(8,0 đ)
Câu 9
a) 5x2 - 5xy + 7y - 7x = 5x(x - y) - 7(x - y) 
 = (x - y).(5x - 7)
1,25đ
b) x2 - y2 + 2x + 1	= (x + 1)2 - y2 
 = (x + y + 1).(x - y + 1)
1,25đ
Câu 10
a) ĐK: x ≠ 0 và x≠ ± 10
1 đ
b) Với x = 2010 thoả mãn ĐKXĐ nên thay x = 2010 vào (*) ta có: 
1đ
Câu 11
B
C
A
E
D
G
H
K
Hình vẽ
0,5 đ
a) Ta có ED, HK lần lượt là đường trung bình của DABC và DGBC nên:
ED = HK (cùng = BC )
ED// HK (cùng // BC) 
ị tứ giác DEHK là hình bình bình hành.
1,0đ
b) Nếu BD ^ CE thì HD ^ EK
ị hình hình hành DEHK có 2 đường chéo vuông góc với nhau nên là hình thoi .
0,75đ
c) * Hình bình hành DEHK là hình chữ nhật ú HD = EK
ú BD = CE
ú DABC cân tại A (một tam giác cân ú có 2 đường trung tuyến bằng nhau)
0,75đ
* Tính diện tích hình chữ nhật DEHK:
SDEHK = ED . EH = BC. AG = 3.2 = (6 cm2)
0,5đ
Đề 2:
Phần I:
Trắc nghiệm
(2,0 đ)
Nội dung
Điểm
Câu
1
2
3
4
5
6
7
8
Mỗi câu 0,25 điểm
Đáp án
C
B
D
B
D
C
B
A
Phần I:
Tự luận
(8,0 đ)
Câu 9
a) 5x2 - 5xy + 7y - 7x = 5x(x - y) - 7(x - y) 
 = (x - y).(5x - 7)
1,25đ
b) x2 - y2 + 2x + 1	= (x + 1)2 - y2 
 = (x + y + 1).(x - y + 1)
1,25đ
Câu 10
a) ĐK: x ≠ 0 và x≠ ± 10
1 đ
b) Với x = 2010 thoả mãn ĐKXĐ nên thay x = 2010 vào (*) ta có: 
1đ
Câu 11
B
C
A
E
D
G
H
K
Hình vẽ
0,5 đ
a) Ta có ED, HK lần lượt là đường trung bình của DABC và DGBC nên:
ED = HK (cùng = BC )
ED// HK (cùng // BC) 
ị tứ giác DEHK là hình bình bình hành.
1,0đ
b) Nếu BD ^ CE thì HD ^ EK
ị hình hình hành DEHK có 2 đường chéo vuông góc với nhau nên là hình thoi .
0,75đ
c) * Hình bình hành DEHK là hình chữ nhật ú HD = EK
ú BD = CE
ú DABC cân tại A (một tam giác cân ú có 2 đường trung tuyến bằng nhau)
0,75đ
* Tính diện tích hình chữ nhật DEHK:
SDEHK = ED . EH = BC. AG = 3.2 = (6 cm2)
0,5đ