Đề kiểm tra kỳ II môn học Toán, khối 11

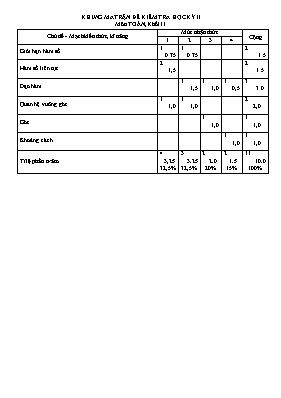
KHUNG MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II 
Môn TOÁN, Khối 11
Chủ đề - Mạch kiến thức, kĩ năng
Mức nhận thức
Cộng
1
2
3
4
Giới hạn hàm số
1 
 0.75
1 
 0.75
2
 1.5
Hàm số liên tục
2
 1,5
2
 1.5
Đạo hàm
1
 1,5
1
 1,0
1
 0,5
3
 3.0
Quan hệ vuông góc
1
 1,0
1
 1,0
2
 2,0
Góc
1
 1,0
1
 1,0
Khoảng cách
1
 1,0
1
 1,0
Tỉ lệ phần trăm
4
 3,25
32,5%
3
 3.25
32,5%
2
 2.0
 20%
2
 1.5
 15%
11
 10.0
100%
ĐỀ CHÍNH THỨC
 (không kể thời gian phát đề)
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT NGUYỄN TRUNG TRỰC
ĐỀ THI HỌC KỲ II, NĂM HỌC 2014 - 2015
 Môn : TOÁN - Khối 11
 Thời gian làm bài: 90 phút
Bài 1 (1,5 điểm). Tính các giới hạn sau:
 a) b) 
Bài 2 (1,5 điểm). Cho hàm số y = .
Xét tính liên tục của tại điểm ;
Xét tính liên tục của trên .
Bài 3 (1,5 điểm). Cho hàm số , chứng minh rằng .
(còn tiếp mặt sau)
 (không kể thời gian phát đề)ĐỀ CHÍNH THỨC
ĐỀ CHÍNH THỨC
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT NGUYỄN TRUNG TRỰC
ĐỀ THI HỌC KỲ II, NĂM HỌC 2014 - 2015
 Môn : TOÁN - Khối 11
 Thời gian làm bài: 90 phút
Bài 1 (1,5 điểm). Tính các giới hạn sau:
 a) b) 
Bài 2 (1,5 điểm). Cho hàm số y = .
Xét tính liên tục của tại điểm ;
Xét tính liên tục của trên .
Bài 3 (1,5 điểm). Cho hàm số , chứng minh rằng .
(còn tiếp mặt sau)
Bài 4 (1,5 điểm). Cho đồ thị (C): ,.
 a) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến này có hệ số góc bằng .
 b) Tìm điểm M thuộc đồ thị (C) sao cho tiếp tuyến của (C) tại M cắt trục tung tại điểm có tung độ bằng -1.
Bài 5 (4 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC); AC = 2a, BC = , SA = a.
Chứng minh 
Chứng minh rằng 
Tính góc giữa hai mặt phẳng (SBC) và (ABC). 
Gọi BH là đường cao kẻ từ B của tam giác ABC, chứng minh và tính khoảng cách giữa hai đường thẳng SC và BH. 
---------------- Hết ---------------
Bài 4 (1,5 điểm). Cho đồ thị (C): ,.
 a) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến này có hệ số góc bằng .
 b) Tìm điểm M thuộc đồ thị (C) sao cho tiếp tuyến của (C) tại M cắt trục tung tại điểm có tung độ bằng -1.
Bài 5 (4 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC); AC = 2a, BC = , SA = a.
Chứng minh 
Chứng minh rằng 
Tính góc giữa hai mặt phẳng (SBC) và (ABC). 
Gọi BH là đường cao kẻ từ B của tam giác ABC, chứng minh và tính khoảng cách giữa hai đường thẳng SC và BH. 
---------------- Hết ---------------
ĐÁP ÁN VÀ BIỂU ĐIỂM MÔN TOÁN KHỐI 11
CÂU
ĐÁP ÁN
ĐIỂM
Bài 1
(1,5 điểm)
a) 
0,25
0,25
0,25
b) 
0,25
 Vì 
0,25
nên .
0,25
Bài 2
(1,5 điểm)
Cho hàm số 
a) Xét tính liên tục của tại điểm .
Tập xác định D = , 
0,25
0,25
0,25
Vì nên liên tục tại điểm (1) 
0,25
b) Xét tính liên tục của trên .
Khi thì , xác định trên khoảng
 liên tục trên khoảng (2) 
0,25
Khi thì , xác định trên khoảng 
liên tục trên khoảng (3) 
Từ (1), (2) và (3) suy ra liên tục trên 
0,25
Bài 3
(1,5 điểm)
Cho hàm số . Chứng minh rằng .
0,25
0,5
0,25
 (ĐPCM)
0,5
Bài 4
(1,5 điểm)
4a) Viết phương trình tiếp tuyến của đồ thị (C): , biết tiếp tuyến này có hệ số góc bằng .
Đặt . Ta có .
0,25
 Tiếp tuyến cần tìm có hệ số góc của bằng -3 
 (với là tọa độ tiếp điểm) 
0,25
0,25
Phương trình tiếp tuyến càn tìm là : .
0,25
4b) Tìm điểm M thuộc đồ thị (C) sao cho tiếp tuyến của (C) tại M cắt trục tung tại điểm có tung độ bằng .
.
Gọi là tiếp tuyến của (C) tại M. Phương trình của là: 
0,25
 cắt trục tung tại điểm có tung độ bằng 
Vậy hoặc .
0,25
Bài 5
(4 điểm)
(1 điểm) Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC); AC = 2a, BC = , SA = a.
a) Chứng minh 
0,5
0,25
0,25
b) (1 điểm) Chứng minh 
0,5
0,25
Mà 
0,25
c) (1 điểm) Tính góc giữa hai mặt phẳng (SBC) và (ABC).
0,5
Tam giác SAB vuông tại A
0,25
Tam giác SAB vuông tại A, có SA = AB 
Vậy = 
0,25
d) (1 điểm) Gọi BH là đường cao kẻ từ B của tam giác ABC, chứng minh và tính khoảng cách giữa hai đường thẳng SC và BH. 
Kẻ HKSC . 
0,25
Đoạn HK là đoạn vuông góc chung của hai đường thẳng BH và SC.
0,25
0,25
Vậy d(BH, SC) 
0,25