Đề kiểm tra học kỳ II (năm 2012 - 2013) môn: Toán lớp 9

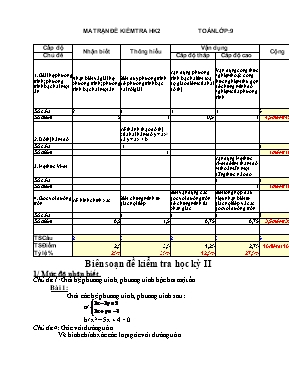
MA TRẬN ĐỀ KIỂM TRA HK2
TOÁN 
LỚP: 9
Cấp độ
Nhận biết
Thông hiểu
Vận dụng
Cộng
Chủ đề
Cấp độ thấp
Cấp độ cao
1. Giải hệ phương trình; phương trình bậc hai một ẩn
Nhận biết và giải hệ phương trình; phương trình bậc hai một ẩn
Biết quy phương trình về phương trình bậc hai rồi giải
Vận dụng phương trình bậc hai tìm toạ độ giao điểm của hai đồ thị
 Vận dụng công thức nghiệm hoặc công thức nghiệm thu gọn để chứng minh số nghiệm của phương trình
Số câu
2
1
 1
 1
5
Số điểm
2
1
0,5 
 1
4,5điểm (45%)
2. Đồ thị hàm số
Vẽ thành thạo đồ thị của hai hàm số y = ax2 và y = ax + b
Số câu
 1
1
Số điểm
1 
1điểm (10%)
3. Hệ thức Vi-ét
Vận dụng Hệ thức Vi-ét để tìm tham số m thoả mãn một đẳng thức nào đó
Số câu
1
1
Số điểm
1
1điểm (10%)
4. Góc với đường tròn
Vẽ hình chính xác
Biết chứng minh tứ giác nội tiếp
Biết vận dụng các góc với đường tròn để chứng minh tia phân giác
Biết tổng hợp dấu hiệu nhận biết tứ giác nội tiếp và các góc với đường tròn
Số câu
1
1
1
3
Số điểm
0,5
1,5
0,75
0,75
3,5điểm (35%)
TS Câu
2
3
2
3
5
TS Điểm
2,5
3,5
1,25
2,75
10điểm (100%)
Tỷ lệ %
25%
35%
12,5%
27,5%
Biên soạn đề kiểm tra học kỳ II
1/ Mức độ nhận biết.
Chủ đề 1: Giải hệ phương trình; phương trình bậc hai một ẩn.
Bài 1: 
Giải các hệ phương trình, phương trình sau:
a/
b/ x2 – 5x + 4 = 0
Chủ đề 4: Góc với đường tròn
 Vẽ hình chính xác các loại góc với đường tròn.
2/ Mức độ thông hiểu 
Chủ đề 1: Giải hệ phương trình; phương trình bậc hai một ẩn.
Bài 1: 
Giải các hệ phương trình, phương trình sau:
c/ x4 – 2x2 – 3 = 0
Chủ đề 2: Đồ thị hàm số
Bài 2: 
Cho hai hàm số (P): y = x2 và (d): y = x + 2.
	a/ Vẽ đồ thị (P) và (d) trên cùng mặt phẳng toạ độ.
Chủ đề 4: Góc với đường tròn
Bài 4: 
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tai H.
a/ Chứng minh các tứ giác BFEC, BFHD nội tiếp.
3/ Mức độ vận dụng
a/ Vận dụng cấp thấp
Chủ đề 1: Giải hệ phương trình; phương trình bậc hai một ẩn.
Bài 2: 
Cho hai hàm số (P): y = x2 và (d): y = x + 2.
b/ Tìm toạ độ giao điểm của (P) và (d) bằng phép tính.
Chủ đề 4: Góc với đường tròn
Bài 4: 
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tai H.
b/ Chứng minh DH là tia phân giác của 
b/ Vận dụng cấp cao
Chủ đề 1: Giải hệ phương trình; phương trình bậc hai một ẩn.
Bài 3: 
Cho phương trình x2 – 2mx – 1 = 0 (m là tham số)
a/ Chứng minh phương trình luôn có hai nghiệm phân biệt.
Chủ đề 3: Hệ thức Vi-ét
Bài 3: 
Cho phương trình x2 – 2mx – 1 = 0 (m là tham số)
 b/ Tìm m để phương trình có hai nghiệm x1, x2 thoả mãn x12 + x22 = 7.
Chủ đề 4: Góc với đường tròn
Bài 4: 
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tai H.
c/ Kẻ AD cắt cung BC tại M. Chứng minh tam giác BMH cân.
ĐỀ KIỂM TRA HỌC KỲ II (2012 - 2013)
Môn: TOÁN – LỚP 9
Thời gian: 90 phút (không kể thời gian phát đề)
Bài 1: (3 điểm)
Giải các hệ phương trình, phương trình sau:
a/
b/ x2 – 5x + 4 = 0
c/ x4 – 2x2 – 3 = 0
Bài 2: (1,5 điểm)
Cho hai hàm số (P): y = x2 và (d): y = x + 2.
	a/ Vẽ đồ thị (P) và (d) trên cùng mặt phẳng toạ độ.
	b/ Tìm toạ độ giao điểm của (P) và (d) bằng phép tính.
Bài 3: (2 điểm)
Cho phương trình x2 – 2mx – 1 = 0 (m là tham số)
a/ Chứng minh phương trình luôn có hai nghiệm phân biệt.
b/ Tìm m để phương trình có hai nghiệm x1, x2 thoả mãn x12 + x22 = 7.
Bài 4: (3,5 điểm)
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tai H.
a/ Chứng minh các tứ giác BFEC, BFHD nội tiếp.
b/ Chứng minh DH là tia phân giác của 
c/ Kẻ AD cắt cung BC tại M. Chứng minh tam giác BMH cân.
ĐÁP ÁN
Bài 1: (3 điểm)
a/ 
Vậy hệ phương trình đã cho có nghiệm là (x;y) = 
(thiếu câu kết luận được tròn điểm)
b/ x2 – 5x + 4 = 0
(a = 1; b = –5; c = 4)
Ta có: a + b + c = 1 + (–5) + 4 = 0
Vậy phương trình đã cho có hai nghiệm: x1 = 1; x2 = 4
(Giải tìm được x1 = 1; x2 = 4, thiếu câu kết luận được tròn điểm)
c/ x4 – 2x2 – 3 = 0
Đặt t = x2, điều kiện t 0. 
Phương trình đã cho trở thành: t2 – 2t – 3 = 0
Giải phương trình ẩn t, tìm được
 t1 = – 1 (loại); t2 = 3 (nhận)
Với t = t2 = 3 x2 = 3 x = hoặc x = – 
Vậy phương trình đã cho có hai nghiệm: x1 = ; x2 = – 
(Thiếu điều kiện t 0 trừ 0,25đ ; thiếu câu kết luận được tròn điểm)
1đ
0,25đ
0,25đ
0,5đ
0,25đ
0,25đ
0,25đ
0,25đ
Bài 2: (1,5 điểm)
a/ (1đ)
- Hàm số: y = x2 
 + Tìm được 5 điểm thuộc đồ thị hay lập bảng giá trị đúng
 + Vẽ đồ thị chính xác
- Hàm số: y = x + 2.
 + Tìm được 2 điểm thuộc đồ thị hay lập bảng giá trị đúng
 + Vẽ đồ thị chính xác
b/ (0,5đ)
Phương trình hoành độ giao điểm của (P) và (d) là:
 x2 = x + 2.
 Giải và tìm được toạ độ giao điểm của (P) và (d) là: (– 1; 1); (2; 4)
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
Bài 3: (2 điểm)
a/ (1đ)
x2 – 2mx – 1 = 0 
 ’ = (–m)2 – 1.(–1) = m2 + 1 > 0 với mọi giá trị m
Vì ’ > 0 với mọi giá trị m
Nên phương trình luôn có hai nghiệm phân biệt.
b/ (1đ)
Theo hệ thức Vi- Ét ta có:
 x1+ x2 = 2m (1)
 x1 . x2 = –1 (2)
Theo đề bài ta có: x12 + x22 = 7 
 (x1 + x2)2 – 2 x1 . x2 = 7 (3)
Thay (1), (2) vào (3) ta được: (2m)2 + 2 = 7
 ...m = hoặc m = 
Vậy để phương trình có hai nghiệm x1, x2 thoả mãn x12 + x22 = 7 thì
 m = hoặc m = 
0,5đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
Bài 4: (3,5 điểm)
Vẽ hình đúng theo đề bài
a/ (1,5đ)
Tứ giác BFEC có
 (do CF AB)
 (do BE AC)
 Hai đỉnh F, E cùng nhìn cạnh BC dưới một góc = 900
 Tứ giác BFEC nội tiếp
Tứ giác BFHD có
 (do CF AB, H CF)
 (do AD BC, H AD)
 Tứ giác BFHD nội tiếp
b/ (0,75đ)
Chứng minh tứ giác DHEC nội tiếp.
Ta có (do BFHD nội tiếp)
 hay (do H BE) (1)
Ta có (do DHEC nội tiếp)
 hay (do H CF) (2)
mà (3)
Từ (1), (2), (3) 
 DH là tia phân giác của 
c/ (0,75đ)
Ta có (các góc nột tiếp cùng chắn )
 hay (do HAM, DBC, EAC)
Ta có (do là góc ngoài tại đỉnh H của tứ giác DHEC nội tiếp)
Do đó 
Vậy BHM cân tại B
0,5đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ