Đề kiểm tra học kỳ I năm học 2016 - 2017 môn Kiểm tra: Toán 9

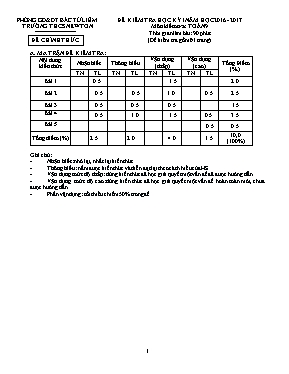
PHÒNG GD&ĐT BẮC TỪ LIÊM
TRƯỜNG THCS NEWTON
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2016 - 2017
Môn kiểm tra: TOÁN 9
Thời gian làm bài: 90 phút
(Đề kiểm tra gồm:01 trang)
A. MA TRẬN ĐỀ KIỂM TRA:
Nội dung
kiến thức
Nhận biết
Thông hiểu
Vận dụng (thấp)
Vận dụng
(cao)
Tổng Điểm (%)
TN
TL
TN
TL
TN
TL
TN
TL
Bài 1
0.5 
 1.5
2.0 
Bài 2
 0.5
 0.5
1.0 
0.5 
2.5
Bài 3
 0.5
0.5
0.5
 1.5
Bài 4
 0.5
1.0
 1.5
0.5 
3.5
Bài 5
 0.5
0.5 
Tổng điểm (%)
 2.5
 2.0
4.0
1.5
10,0
(100%)
Ghi chú:
Nhận biết: nhớ lại, nhắc lại kiến thức
Thông hiểu: nắm được kiến thức và diễn đạt lại theo cách hiểu của HS
Vận dụng mức độ thấp: dùng kiến thức đã học giải quyết một vấn đề đã được hướng dẫn.
Vận dụng mức độ cao: dùng kiến thức đã học giải quyết một vấn đề hoàn toàn mới, chưa được hướng dẫn.   
Phần vận dụng: tối thiểu chiếm 50% trong đề.
B. ĐỀ KIỂM TRA
Bài I (2,0 điểm)
 Cho biểu thức và với 
Tính giá trị của biểu thức khi .
Rút gọn biểu thức .
Tìm để giá trị của biểu thức .
Bài II ( 2,5 điểm) Cho hàm số có đồ thị là (dm).
Tìm biết (dm) song song với đường thẳng .
Vẽ đồ thị hàm số với .
Với , (dm) cắt trục hoành tại A và cắt trục tung tại B. Tìm để diện tích tam giác OAB đạt giá trị nhỏ nhất.
Bài III ( 1,5 điểm) Cho tam giác vuông tại có , BC = 10cm.
1) Tính , .	 
2) Kẻ đường cao của tam giác, tính .
( Kết quả làm tròn đến hàng phần trăm )
Bài IV (3,5 điểm) Cho nửa đường tròn (O) đường kính AB. Điểm M di chuyển trên nửa đường tròn. Tiếp tuyến tại M và B của nửa đường tròn (O) cắt nhau ở D. Qua O kẻ đường thẳng song song với MB, cắt tiếp tuyến tại M ở C và cắt tiếp tuyến tại B ở N.
Chứng minh các điểm O, M, D, B cùng thuộc một đường tròn. 
Chứng minh tam giác CDN cân.
Chứng minh AC là tiếp tuyến của nửa đường tròn (O) và tích AC.BD không đổi.
Tìm vị trí của M trên nửa đường tròn để diện tích tam giác CDN đạt giá trị nhỏ nhất.
Bài V ( 0,5 điểm) Gải phương trình 
................................ Hết ...................................
Giáo viên ra đề
(Ghi rõ họ, tên, ký)
Nguyễn Văn Phùng
Tổ trưởng chuyên môn
(Ghi rõ họ, tên, ký)
Phạm Thị Thanh
Hiệu trưởng
(Ghi rõ họ, tên, ký)
PHÒNG GD&ĐT BẮC TỪ LIÊM
TRƯỜNG THCS NEWTON
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM 
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2016 - 2017
Môn kiểm tra: TOÁN
Thời gian làm bài: 90 phút
I. Hướng dẫn chung
- Bài 1. 
- Bài 2. 
+ý 1: HS không kết luận trừ 0,25.
+HS vẽ đồ thị thiếu các kí hiệu O, x, y trừ 0,25đ.
- Bài 3. HS không làm tròn kết quả như yêu cầu trừ 0,5 đ toàn bài.
- Bài 4. HS không vẽ hình thì không chấm điểm.
- Bài 5. HS làm bài 5 theo công thức nghiệm để giải PT bậc 2 vẫn cho điểm tối đa. HS có thể làm theo cách đặt ẩn phụ đưa về pt, hpt hoặc cách khác vẫn đc điểm tối đa.
II. Đáp án và thang điểm:
Câu
Nội dung
Điểm
1
 Cho biểu thức và với 
Tính giá trị của biểu thức khi .
Rút gọn biểu thức .
Tìm để giá trị của biểu thức .
1) 
0.5
2) 
1,0
3) 
 (tmđk)
Vậy, ..
0,5
2
Cho hàm số có đồ thị là (dm).
Tìm biết (dm) song song với đường thẳng (d).
Vẽ đồ thị hàm số với .
Với , (dm) cắt trục hoành tại A và cắt trục tung tại B. Tìm để diện tích tam giác OAB đạt GTNN.
1) .
Vậy .
1,0
2) Với , ta có hàm số: (d’).
+Cho , (d’) cắt Oy tại điểm (0;-1).
 Cho , (d’) cắt Ox tại điểm .
+ Vẽ đồ thị 
0,25
0,25
0,5
3)
+ Với , (dm) cắt trục hoành tại , cắt trục tung tại .
+ Diện tích tam giác OAB:
Dấu bằng xảy ra khi và chỉ khi . 
Vậy diện tích tam giác OAB nhỏ nhất bằng 2 khi 
0,25
0,25
3
Cho tam giác ABC vuông tại A có , BC = 10cm.
a) Tính AB, AC.	 
b) Kẻ đường cao AH của tam giác, tính AH.
( Kết quả chính xác đến hàng phần trăm )
a) 
.
b) AH.BC=AB.AC è 
 (cm)
0,5
0,5
0,5
4
Cho nửa đường tròn (O) đường kính AB. Điểm M di chuyển trên nửa đường tròn. Tiếp tuyến tại M và B của nửa đường tròn (O) cắt nhau ở D. Qua O kẻ đường thẳng song song với MB, cắt tiếp tuyến tại M ở C và cắt tiếp tuyến tại B ở N.
1) Chứng minh các điểm O, M, D, B cùng thuộc một đường tròn. 
2) Chứng minh tam giác CDN cân.
3) Chứng minh AC là tiếp tuyến của nửa đường tròn (O) và tích AC.BD không đổi.
4) Tìm vị trí của M trên nửa đường tròn để diện tích tam giác CDN đạt giá trị nhỏ nhất.
0,25
1) Cùng thuộc đường tròn đường kính OD.
0,75
2)
 + Chứng minh tam giác DMB cân tại D è góc DMB=góc DBM
+ NC//MB è góc DCN = góc DNC 
1,0
3) 
+ Chứng minh CO=ON
+ Từ đó chứng minh được tam giác COA = tam giác NOB
+ Suy ra: CAO =900. Hay CA là tiếp tuyến.
1,0
4) 
+ Diện tích tam giác CDN bằng 2 lần diện tích tam giác COD
+ Diện tích tam giác COD bằng: ½.OM.CD nhỏ nhất khi CD nhỏ nhất
+ CD nhỏ nhất bằng AB khi CD vuông góc với AC. Khi đó M là điểm chính giữa của cung AB.
0,5
5
Gải phương trình 
+ Điều kiện: 
+ 
0,5
Giáo viên ra đề
(Ghi rõ họ, tên, ký)
Nguyễn Văn Phùng
Tổ trưởng chuyên môn
(Ghi rõ họ, tên, ký)
Phạm Thị Thanh
Hiệu trưởng
(Ghi rõ họ, tên, ký)