Đề kiểm tra học kỳ 1 môn Toán Lớp 12 - Năm học 2016-2017 - Trường THPT Bình Thủy (Có đáp án)

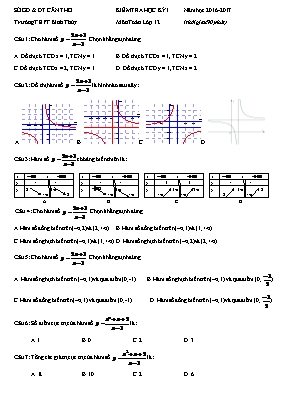
SỞ GD & ĐT CẦN THƠ	KIỂM TRA HỌC KỲ I 	Năm học 2016-2017
Trường THPT Bình Thủy	Môn Toán Lớp 12 	(thời gian 90 phút)
Câu 1: Cho hàm số . Chọn khẳng định đúng.
A. Đồ thị có TCĐ x = 1, TCN y = 1.	B. Đồ thị có TCĐ x = 1, TCN y = 2.
C. Đồ thị có TCĐ x = 2, TCN y = 1.	D. Đồ thị có TCĐ y = 1, TCN x = 2.
Câu 2: Đồ thị hàm số là hình nào sau đây:
 A. B. C. D. 
Câu 3: Hàm số có bảng biến thiên là: 
x
 1 
y’
 -
y
2 +∞
 -∞ 2
 A
x
 1 
y’
 -
y
 +∞
 -∞ -∞
 B
x
 1 
y’
 + +
y
 +∞ +∞
 -∞ -∞
 C
x
 1 
y’
 -
y
 +∞ 2
 2 -∞ 
 D
 Câu 4: Cho hàm số . Chọn khẳng định đúng.
A.Hàm số đồng biến trên (-∞;2)và (2;+∞)	B. Hàm số đồng biến trên (-∞;1)và (1;+∞)
C. Hàm số nghịch biến trên (-∞;1)và (1;+∞)	D. Hàm số nghịch biến trên (-∞;2)và (2;+∞)
Câu 5: Cho hàm số . Chọn khẳng định đúng.
A. Hàm số nghịch biến trên (-∞;1) và qua điểm (0;-1) B. Hàm số nghịch biến trên (-∞;1) và qua điểm (0; )
C. Hàm số đồng biến trên (-∞;1) và qua điểm (0;-1)	D. Hàm số đồng biến trên (-∞;1) và qua điểm (0; )
Câu 6: Số điểm cực trị của hàm số là:
 	A.1	B. 0	C. 2	D. 3
Câu 7: Tổng các giá trị cực trị của hàm số là:
8	B. 10	C. 2	D. 6
Câu 8: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [0; 3].
A. 2; 	B. ; 2	C. 0; 	D. ; 0
Câu 9: Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [0; 3].
A. 	B. 	C. 	D. 
Câu 10: Cho hàm số có đồ thị (C) như hình bên.
 Chọn khẳng định đúng:
Hàm số đồng biến trên khoảng (0;+∞).
Hàm số nghịch biến trên khoảng (0;+∞).
Hàm số đồng biến trên khoảng ( – ∞;0).
Hàm số nghịch biến trên khoảng ( – ∞;0).
Câu 11: Cho hàm số có đồ thị (C) như hình bên.
 Chọn khẳng định đúng:
Hàm số đạt cực đại tại x = 0.
Hàm số đạt cực tiểu tại x = 0.
Hàm số đạt cực đại tại y = 0.
Hàm số đạt cực tiểu tại y = 0.
Câu 12: Cho hàm số có đồ thị (C) như hình bên.
 Chọn khẳng định đúng:
Hàm số đạt cực đại tại x = 0 và đồng biến (0;+∞).
Hàm số đạt cực tiểu tại x = 0 và đồng biến (0;+∞).
Hàm số đạt cực đại tại x = 1, nghịch biến ( – ∞;-1).
Hàm số đạt cực tiểu tại x = 1 và đồng biến (1;+∞).
Câu 13: Cho hàm số có đồ thị (C) như hình bên.
 Chọn khẳng định đúng:
Điểm cực đại (0;-1) và đồng biến (2;+∞).
Điểm cực tiểu (2;-5) và đồng biến ( – ∞;-2).
Điểm cực đại (0;-1) và nghịch biến (2;+∞).
Điểm cực tiểu (-2;-5) và đồng biến ( – ∞;-2).
Câu 14: Đồ thị hình bên là của hàm số nào:
 Chọn khẳng định đúng:
Câu 15: Bảng biến thiên hình bên là của hàm số nào:
 Chọn khẳng định đúng:
 B.
C. D.
Câu 16: Một người muốn sau 4 tháng có 1 tỷ đồng để xây nhà. Hỏi người đó phải gửi mỗi tháng là bao nhiêu tiền (như nhau). Biết lãi suất 1 tháng là 1%. (đơn vị tỷ đồng)
A. 	B. 	C. 	D. 
Câu 17: Cho , tính theo a.
A. 	B. 	C. 	D. 
Câu 18: 
Hãy xác định để hàm số có đồ thị như hình vẽ
x
y
-3
4
3
2
-2
-2
O
A. 
B. 
C. 
D. 
Câu 19: Hệ số góc của tiếp tuyến của đồ thị hàm sốtại điểm có hoành độ x = 1.
ln5 + 2	B. ln3 + 2	C. ln5 - 2	D. ln3 – 2
Câu 20: Giải phương trình: 
	B. 	C. 	D. 
Câu 21: Ph­¬ng tr×nh cã nghiÖm lµ:	
A. 	B. 	C. 	D. 2
Câu 22: Tìm m để hàm số chỉ có cực tiểu mà không có cực đại.
Câu 23: Ph­¬ng tr×nh: cã nghiÖm lµ:	
A. 0	B. 1	C. 2	D. 3
Câu 24: Ph­¬ng tr×nh: cã nghiÖm lµ:
A. 24	B. 36	C. 45	D. 64
Câu 25: Giải phương trình: 
A. 	B.x=1	C. x = 4	D. 
Câu 26: Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng . Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất. 
A. x = 10m, y = 5m, 	B. x = 10m, y = 5m, 
C. x = 7m, y = 8m, 	D.x = 10m, y = 5m, 
Câu 27: Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng .
A. m (-2; 2)	B. m (-¥: 2] È [2; +¥)	C. m(-¥: 2	D. mR\{-2; 2}
Câu 28: Một mặt phẳng qua trục của hình trụ và cắt hình trụ theo thiết diện là hình vuông cạnh bằng 2a. Tính theo a diện tích toàn phần của hình trụ.
A. 	B. 	C. 	D. 
Câu29: Hàm số y = có tập xác định là:
	A. R	B. (0; +¥))	C. R\	D. 
Câu 30: Hàm số y = có tập xác định là:
	A. (-2; 2)	B. (-¥: 2] È [2; +¥)	C. R	D. R\{-2; 2}
Câu 31: Hàm số y = có tập xác định là:
	A. R	B. (1; +¥)	C. (-1; 1)	D. R\{-1; 1}
Câu 32:Hàm số: xác định khi:
A.-53; B.-3<x<3; C.x<-5; D.-5<x<3
Câu 33: Hàm số: xác định khi:
A.x2; B.12; D.<x<2
Câu 34: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, O = AC Ç BD. Tính độ dài SO của hình chóp
A. 	B. 	C. a	D. 
Câu 35: Cho lăng trụ tam giác đều , cạnh đáy bằng a. Gọi M, N, I lần lượt là trung điểm của AA’, AB, BC; O là trọng tâm DABC; CC’ = . Thể tích của khối lăng trụ là
	A. 	B. 	C. 	D. 
Câu 36. Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức 1,05%. Theo số liệu của Tổng Cục Thống Kê, dân số của Việt Nam năm 2014 là 90.728.900 người. Với tốc độ tăng dân số như thế thì vào năm 2030 thì dân số của Việt Nam là bao nhiêu?
A. 107232573 người	B. 107232574 người	C. 105971355 người	D. 106118331 người
C©u 37: Hµm sè y = cã tËp x¸c ®Þnh lµ:
A. (-¥; -2)	B. (1; +¥)	C. (-¥; -2] È (2; +¥)	D. (-2; 2)
Câu 38: Cho lăng trụ tam giác đều , cạnh đáy bằng a. Gọi M, N, I lần lượt là trung điểm của AA’, AB, BC; O là trọng tâm DABC; CC’ = . Tính VC’NAI 
A. V = 	B. V = 	C. V = 	D. V = 
C©u 39: Hµm sè y = cã tËp x¸c ®Þnh lµ:
A. (0; +¥)\ {e}	B. (0; +¥)	C. R	D. (0; e)
Câu 40: Một mặt phẳng qua trục của hình trụ và cắt hình trụ theo thiết diện là hình vuông cạnh bằng 2a. Tính theo a thể tích của khối trụ.
A. 	B. 	C. 	D. 
C©u 41: Cho pa > pb. KÕt luËn nµo sau ®©y lµ ®óng?
	A. a b 	C. a + b = 0	D. a.b = 1
C©u 42: Cho K = . biÓu thøc rót gän cña K lµ:
	A. x	B. 2x	C. x + 1	D. x - 1
Câu 43: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, đường thẳng SA vuông góc với mặt phẳng (ABCD), đường thẳng SC tạo với mặt phẳng (ABCD) một góc bằng . Gọi E là trung điểm của cạnh SC. Tính theo a thể tích của khối chóp S.ABCD.
A. 	B. 	C. 	D. 
C©u 44: Tìm m để hàm số đạt cực tiểu tại điểm 	
C©u 45: Trong các tiếp tuyến tại các điểm trên đồ thị hàm số , đường thẳng nào sau đây là tiếp tuyến có hệ số góc nhỏ nhất: 
A. y= x+1	 B. y= 4x+3 C. y= 4x. D. y= x+3 
C©u 46: Cho hàm số: Phương trình tiếp tuyến của tại giao điểm của với trục tung là:
A. 	B. 	C. 	D. 
Câu 47: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, đường thẳng SA vuông góc với mặt phẳng (ABCD), đường thẳng SC tạo với mặt phẳng (ABCD) một góc bằng . Gọi E là trung điểm của cạnh SC. Tính theo a Khoảng cách từ điểm E đến mặt phẳng (SAD).
A. 	B. 	C. 	D. 
C©u 48: Cho log. Khi ®ã tÝnh theo a vµ b lµ:
	A. 	B. 	C. a + b	D. 
C©u 49: Gi¶ sö ta cã hÖ thøc a2 + b2 = 7ab (a, b > 0). HÖ thøc nµo sau ®©y lµ ®óng?
	A. 	B. 
	C. 	D. 4
Câu 50: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, đường thẳng SA vuông góc với mặt phẳng (ABCD), đường thẳng SC tạo với mặt phẳng (ABCD) một góc bằng . Gọi E là trung điểm của cạnh SC. Tính theo a thể tích của khối tứ diện EACD.
A. 	B. 	C. 	D. 
ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
D
A
C
A
C
D
B
D
C
A
D
A
B
C
D
A
D
A
B
A
A
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
D
C
B
C
A
B
A
C
A
C
B
C
A
C
B
B
D
B
C
C©u6: Ph­¬ng tr×nh: cã nghiÖm lµ:	A. -3	B. 2	C. 3	D. 5
C©u7: TËp nghiÖm cña ph­¬ng tr×nh: lµ:	A. 	B. 	C. 	D. 
C©u8: Ph­¬ng tr×nh: cã nghiÖm lµ:	A. 1	B. 2	C. 3	D. 4
C©u3: BÊt ph­¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. (0; 1)	D. 
C©u9: BÊt ph­¬ng tr×nh: cã tËp nghiÖm lµ:
	A. 	B. 	C. (-1; 2)	D. (-¥; 1)
Câu 11.Tập xác định của hàm số: là:
A.x>0; B.x0; D.-2<x<0
Câu 17.Hàm số: xác định khi:
A.x>1; 	B.x>2; 	C.x<1; 	D.x<2
Câu 21. Hàm số: xác định khi:
A. (2; 3)	B. 	C. 	D. (-¥; -6) È (1; +¥)