Đề kiểm tra học kỳ 1 môn Toán học 9 năm học 2016 - 2017

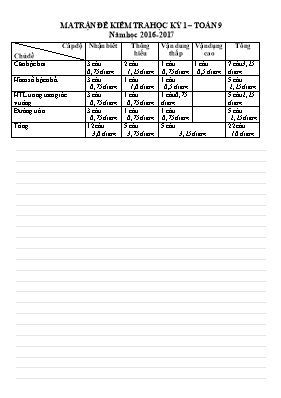
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ 1 – TOÁN 9
Năm học 2016-2017
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dung thấp
Vận dụng cao
Tổng
Căn bậc hai
3 câu
0,75 điểm
2 câu
1,25 điểm
1 câu
0,75 điểm
1 câu
0,5 điểm
7 câu3,25 điểm
Hàm số bậc nhất
3 câu
0,75 điểm
1 câu
 1,0 điểm
1 câu
0,5 điểm
5 câu
2,25 điểm
HTL trong tam giác vuông
3 câu
0,75 điểm
1 câu
0,75 điểm
1 câu0,75 điểm
5 câu2,25 điểm
Đường tròn
3 câu
0,75 điểm
1 câu
0,75 điểm
1 câu
0,75 điểm
5 câu
2,25 điểm
Tổng
12 câu
3,0 điểm
5 câu
3,75 điểm
5 câu
3,25 điểm
22 câu
10 điểm
....................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
PHÒNG GIÁO DỤC ..
TRƯỜNG THCS .
ĐỀ KIỂM TRA HỌC KỲ 1
MÔN TOÁN LỚP 9 – Năm học: 2016 - 2017
Thời gian làm bài 90 phút
Tự luận (10,0 điểm).
Câu 1(1,5 điểm): 
a)Cho và . Tính A.B
b)Tìm x biết 
Câu 2(2,0 điểm): Cho biểu thức 
a) Tìm ĐKXĐ, rút gọn P
b) Tìm giá trị nhỏ nhất của P
c) Tìm x để biểu thức nhận giá trị nguyên.
Câu 3(1,5 điểm):
a) Cho hàm số y = 3x + 4(d) vẽ đồ thị hàm số trên và xác định góc tạo bởi đường thẳng (d) và trục Ox.
b) Tìm giá trị của m biết đường thẳng y = 2x – 3 và đường thẳng y = (m- 1)x + m- 2 cắt nhau tại một điểm trên trục tung.
Câu 3(4,0 điểm): 
Cho đường tròn (O; R) đường kính AB. Từ A và B kẻ các tiếp tuyến Ax và By với đường tròn (Ax, By cùng thuộc nửa mặt phẳng bờ AB). Trên tia Ax lấy điểm C, qua C kẻ tiếp tuyến CD với đường tròn(D là tiếp điểm) cắt tia By tại E. Gọi H là giao điểm của OC và AD.
a) Chứng minh rằng H là trung điểm của AD.
b) Tính số đo góc COE, từ đó suy ra AC.BE = R2.
c) Chứng minh rằng AB là tiếp tuyến của đường tròn đường kính CE.
d) Xác định vị trí của điểm C trên tia Ax để tứ giác ABEC có chu vi nhỏ nhất.
Câu 4(1.0 điểm): Cho a, b > 0 và ab ≥ 1. Chứng minh rằng:
-----------------------------------------------Hết-----------------------------------------------
HƯỚNG DẪN CHẤM BÀI KIỂM TRA HỌC KỲ I–MÔN TOÁN 9
(Hướng dẫn chấm gồm 2 trang)
Bài
Đáp án
Điểm
Câu 1
(1,5 điểm)
a) 0,5 điểm
0,25
Suy ra A.B = 
0,25
b) 0,5 điểm
Điểu kiện x ≥ 0
0,25
0,25
Vậy x = 
c) 0,5 điểm
Điểu kiện x ≥ 0 và x ≠ 1
0,25
0,25
Vậy giá trị biểu thức không phụ thuộc vào x
Câu 2
(2.0 điểm)
Câu 3
(1,5 điểm)
a) 1,0 điểm
 Ta thấy hàm số y = 3x + 4 luôn xác định với ∀x∈R
Cho x = 0 y = 4 nên A(0;4) ∈ox
Cho y = 0 x= nên B(;0) ∈ oy
0,25
Vậy đồ thị của hàm số y = 3x + 4 là một đường thẳng đi qua hai điểm
A(0;4) và B(;0)
0,25
0,25
Gọi là góc tạo bởi đường thẳng (d) và trục Ox
Ta có: 
0,25
b) 0,5 điểm
Vì đường thẳng y = 2x – 3 và đường thẳng y = (m- 1)x + m- 2 cắt nhau tại một điểm trên trục tung, suy ra 
0,25
Vậy m = -1
0,25
Câu 3
(4,0 điểm)
0,25
a) 1.0 điểm
DAOD cân tại O (vì OA = OD) mà OC hay OH là phân giác của góc AOD (vì CA, CD là 2 tiếp tuyến cắt nhau tại C)
0,5
nên OH là trung tuyến của DAOD.
0.25
Vậy H là trung điểm của AD
0,25
b) 1.0 điểm
Ta có OE là tia phân giác của góc BOD (vì ED và EB là 2 tiếp tuyến cắt nhau tại E), OC là tia phân giác của góc AOD (cmt), 
mà và kề bù nên OE vuông góc với OC hay 
0,5
Cũng theo t/c hai tiếp tuyến cắt nhau, ta có: ED = EB; CA = CD (1)
0,25
mặt khác DCOE vuông tại O, OD ^CE (vì CE là tiếp tuyến đường tròn (O)) theo HTL trong tam giác vuông ta có CD. DE = OD2 = R2 (2)
0,25
Từ (1) và (2) suy ra AC. BE = R2.
c) 1.0 điểm
Gọi I là trung điểm của CE, tứ giác ABEC là hình thang (AC// EB do cùng ^ AB), 
0,25
mà O là trung điểm AB nên OI là đường trung bình của hình thang ABEC Þ OI // AC mà AC ^ AB Þ OI ^ AB tại O (3)
0.25
Mặt khác DCEO vuông tại O có OI là trung tuyến Þ OI = (4)
0,25
Từ (3) và (4) Þ AB là tiếp tuyến đường tròn đường kính CE (đpcm)
0,25
d)1.0 điểm
 Chu vi tứ giác ABEC = AB + AC + CE + BE = AB + 2CE,
Chu vi tứ giác ABEC nhỏ nhất suy ra CE nhỏ nhất, mà CE ≥ AB, CE nhỏ nhất khi CE = AB Þ Tứ giác ABEC là hình chữ nhật và OI = .
0,25
0.25
0,25
Do A không đổi, tia Ax cố định và CA = R không đổi nên C nằm trên tia Ax cách A một khoảng bằng R thì chu vi tứ giác ABEC nhỏ nhất.
0,25
Câu 4
(1.0 điểm)
BĐT cuối đúng với a, b > 0 và ab ≥ 1 Þ đpcm
0,5
0,5