Đề kiểm tra học kỳ 1 môn Toán 8 - Năm học 2015 – 2016

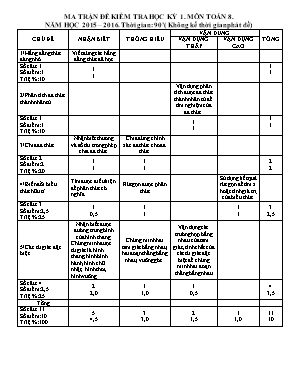
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ 1. MÔN TOÁN 8.
NĂM HỌC 2015 – 2016. Thời gian: 90’( Không kể thời gian phát đề)
CHỦ ĐỀ
NHẬN BIẾT
THÔNG HIỂU
VẬN DUNG
TỔNG
VẬN DỤNG THẤP
VẬN DỤNG CAO
1/ Hằng đẳng thức đáng nhớ
Viết đúng các hằng đẳng thức đã học
Số câu: 1
Số điểm: 1
Tỉ lệ %: 10
1
1
1
1
2/ Phân tích đa thức thành nhân tử
Vận dụng phân tích được đa thức thành nhân tử để tìm nghiệm của đa thức.
Số câu: 1
Số điểm: 1
Tỉ lệ %: 10
1
1
1
1
3/ Chia đa thức
Nhận biết thương và số dư trong phép chia đa thức.
Chia đúng chính xác đa thức cho đa thức. 
Số câu: 2
Số điểm: 2
Tỉ lệ %: 20
1
1
1
1
2
2
4/ Biến đổi biểu thức hữu tỉ
Tìm được điều kiện để phân thức có nghĩa.
Rút gọn được phân thức
Sử dụng kết quả rút gọn để tìm x hoặc tính giá trị của biểu thức.
Số câu: 3
Số điểm: 2,5
Tỉ lệ %: 25
1
0,5
1
1
1
1
3
2,5
5/ Các tứ giác đặc biệt. 
Nhận biết được đường trung bình của hình thang.
Chứng minh được tứ giác là hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông.
Chứng minh hai tam giác bằng nhau, hai đoạn thẳng bằng nhau, vuông góc.
Vận dụng các trường hợp bằng nhau của tam giác, tính chất của các tứ giác đặc biệt để chứng minh hai đoạn thẳng bằng nhau
Số câu: 4
Số điểm: 2,5
Tỉ lệ %: 25
2
2,0
1
1,0
1
0,5
4
3,5
Tổng
Số câu: 11
Số điểm: 10
Tỉ lệ %: 100
5
4,5
3
3,0
2
1,5
1
1,0
11
10
TRƯỜNG THCS ĐINH TIÊN HOÀNG
TỔ TOÁN LÝ
KIỂM TRA HỌC KỲ 1
MÔN TOÁN 8.
NĂM HỌC 2015 – 2016.
ĐỀ CHÍNH THỨC
Câu 1: ( 2,0 điểm) 
a) Viết hai hằng đẳng thức bất kỳ trong số 7 hằng đẳng thức đã học.
b) Tìm x, biết: .
Câu 2: ( 2,0điểm) Cho đa thức . 
Chia đa thức P(x) cho x – 1.
b) Hãy chỉ ra thương và số dư trong phép chia trên. 
Câu 3: ( 2,5 điểm) Cho phân thức: 
Tìm điều kiện của x để A có nghĩa.
Rút gọn A.
Tìm các giá trị nguyên của x để A có giá trị nguyên.
Câu 4: (1,0 điểm) Cho hình thang ABCD( AB // CD) có . Gọi M là trung điểm của cạnh bên BC. Chứng minh rằng MA = MD.
Câu 5: ( 2,5 điểm) Cho hình vuông ABCD. Gọi E, F lần lượt là trung điểm của AB và BC; M là giao điểm của CE và DF.
Chứng minh rằng . Từ đó chứng minh rằng .
Gọi I là trung điểm của CD. Tứ giác AICE là hình gì?
Chứng minh rằng AM = AB.
--HẾT--
ĐỀ CHÍNH THỨC
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ I. MÔN TOÁN 8
NĂM HỌC 2015 – 2016.
CÂU
ĐÁP ÁN
ĐIỂM
1
a)
Viết đúng 2 trong số 7 hằng đẳng thức sau: 
0,5
0,5
b)
0,5
0,5
2
a) 
1
b)
Thương của phép chia: 
Dư của phép chia : 3
0,5
0,5
3
a) 
Điều kiện xác định: . 
0,5
b) 
Rút gọn: 
0,5
0,5
c) 
0,5
0,5
4
Kẻ MH AD. Ta có: MH // AB và MB = MC. 
Suy ra: HA = HD.
Do đó, MH là đường trung trực của đoạn thẳng AD. Nên MA = MD
0,5
0,5
5
a)
Ta có: BCE = CDF(2 cạnh góc vuông)
. Do đó, Suy ra: . Vậy, CE DF.
0,5
0,5
b)
Ta có: AE = CI ; AE // CI suy ra: AICE là hình bình hành
0,5
c) 
Ta có: AI // CE nên AI DF. Mà tam giác MCD vuông tại M có MI là đường trung tuyến ứng với cạnh huyền CD nên IM = ID.
Suy ra, IA là đường trung trực của đoạn thẳng DM. 
Hay, AM = AD = AB. 
0,5
0,5
Ghi chú: Hs giải cách khác nhưng đúng thì vẫn cho điểm tối đa.
TRƯỜNG THCS ĐINH TIÊN HOÀNG
TỔ TOÁN LÝ
KIỂM TRA HỌC KỲ 1
MÔN TOÁN 8.
NĂM HỌC 2015 – 2016.
ĐỀ DỰ BỊ
Câu 1: ( 2,0 điểm) 
a) Viết hai hằng đẳng thức bất kỳ trong số 7 hằng đẳng thức đã học.
b) Tìm x, biết: .
Câu 2: ( 2,0điểm) Cho đa thức . 
Chia đa thức P(x) cho x +2.
b) Hãy chỉ ra thương và số dư trong phép chia trên. 
Câu 3: ( 2,5 điểm) Cho phân thức: 
Tìm điều kiện của x để A có nghĩa.
Rút gọn A.
Tìm các giá trị nguyên của x để A có giá trị nguyên.
Câu 4: (1,0 điểm) Cho hình thang MNPQ( MN // PQ) có . Gọi K là trung điểm của cạnh bên NP. Chứng minh rằng KM = KQ.
Câu 5: ( 2,5 điểm) Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB và BC; I là giao điểm của CM và DN.
Chứng minh rằng . Từ đó chứng minh rằng .
Gọi O là trung điểm của CD. Tứ giác AOCM là hình gì?
Chứng minh rằng AI = AB.
--HẾT--
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ I. MÔN TOÁN 8
ĐỀ DỰ BỊ
NĂM HỌC 2015 – 2016.
CÂU
ĐÁP ÁN
ĐIỂM
1
a)
Viết đúng 2 trong số 7 hằng đẳng thức sau: 
0,5
0,5
b)
0,5
0,5
2
a)
1
b)
Thương của phép chia: 
Dư của phép chia : 0
0,5
0,5
3
a) 
Điều kiện xác định: 
0,5
b) 
Rút gọn: 
0,5
0,5
c) 
0,5
0,5
4
Kẻ KH AD. Ta có: KH // MN 
và KN = KP. 
Suy ra: HM = HN.
Do đó, KH là đường trung trực của đoạn thẳng MN. Nên KM = KN
0,5
0,5
5
a)
Ta có: BCM = CDN(2 cạnh góc vuông)
. Do đó, Suy ra: . Vậy, CM DN.
0,5
0,5
b)
Ta có: AM = CO ; AM // CO suy ra: AOCM là hình bình hành
0,5
c) 
Ta có: AO // CM nên AO DN. Mà tam giác ICD vuông tại I có IO là đường trung tuyến ứng với cạnh huyền CD nên OI = OD.
Suy ra, OA là đường trung trực của đoạn thẳng DI. 
Hay, AI = AD = AB. 
0,5
0,5
Ghi chú: Hs giải cách khác nhưng đúng thì vẫn cho điểm tối đa.