Đề kiểm tra học kì II môn học Toán 11

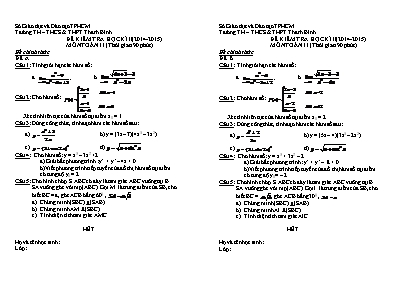
Sở Giáo dục và Đào tạo TPHCM	
Trường TH – THCS & THPT Thanh Bình
ĐỀ KIỂM TRA HỌC KÌ II(2014-2015)
	MÔN TOÁN 11 (Thời gian 90 phút)
Đề chính thức
ĐỀ A
Câu 1: Tính giới hạn các hàm số:
 a. ;	 b. 
Câu 2: Cho hàm số: 
Xét tính liên tục của hàm số tại điểm x0 = 1
Câu 3: Dùng công thức, tính đạo hàm các hàm số sau:
a) 	b) y = (3x – 7)(4x3 – 3x2) 
c) 	d) 
Câu 4: Cho hàm số: y = x3 – 3x2 +2 
	 a) Giải bất phương trình : y” + y’ – 4x < 0
b)Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm 
có tung độ y0 = 2
Câu 5: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B. 
SA vuông góc với mp(ABC) .Gọi M là trung điểm của SB, cho biết BC = a, góc ACB bằng 600 , 
Chứng minh (SBC)(SAB)
Chứng minh AM(SBC)
Tính diện tích tam giác AMC.
HẾT
Họ và tên học sinh:
Lớp:
Sở Giáo dục và Đào tạo TPHCM	
Trường TH – THCS & THPT Thanh Bình
ĐỀ KIỂM TRA HỌC KÌ II(2014-2015)
	MÔN TOÁN 11 (Thời gian 90 phút)
Đề chính thức
ĐỀ B
Câu 1: Tính giới hạn các hàm số:
 a. ;	 b. 
Câu 2: Cho hàm số: 
Xét tính liên tục của hàm số tại điểm x0 = 2
Câu 3: Dùng công thức, tính đạo hàm các hàm số sau:
a) 	b) y = (5x – 4)(3x3 – 2x2) 
c) 	d) 
Câu 4: Cho hàm số: y = x3 + 3x2 – 2 
	 a) Giải bất phương trình : y” + y’ – 8 < 0
b)Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm 
có tung độ y0 = – 2
Câu 5: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B. 
SA vuông góc với mp(ABC) .Gọi I là trung điểm của SB, cho biết BC = , góc ACB bằng 300 , 
Chứng minh (SBC)(SAB)
Chứng minh AI(SBC)
Tính diện tích tam giác AIC.
HẾT
Họ và tên học sinh:
Lớp:
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP HỒ CHÍ MINH
TRƯỜNG TH – THCS& THPT THANH BÌNH
HƯỚNG DẪN CHẤM MÔN TOÁN 11 HỌC KỲ II (2014-2015)
ĐỀ A
CÂU
NỘI DUNG
ĐIỂM
1
Tính giới hạn các hàm số:
	=2đ
a) 
=1đ
0,5đ
0,25đ
0,25đ
b) 
=1đ
0,25đ
0,25đ+0,25đ
0,25đ
0,25đ
2
=1đ
f(1) = 
0,25đ
0,25đ+0,25
 nên hs liên tục tại x0 = 1
0,25đ
3
Dùng công thức, tính đạo hàm các hàm số sau:
=2đ
a) 
=0,5đ	
0,25đ
0,25đ
b) y = (3x – 7)(4x3 – 3x2) 
=0,5đ
y’ = (3x – 7)’(4x3 – 3x2) +(4x3 – 3x2)’ (3x – 7)
0,25đ
y’ = 3(4x2 – 3x2) +( 12x2 – 6x )(3x – 7)
 = –48x3 – 15x2 + 42x
0,25đ
c) 
=0,5đ
y’= 4(5+cos2x)’(5+ cos2x)3
 = – 4(2x)’sin2x(5 + cos2x)3
0,25đ
 = – 8sin2x(5 + cos2x)3
0,25đ
d) 
=0,5đ
0,25đ
0,25đ
3
y = x3 – 3x2 +2
=2đ
 a) Giải bất phương trình : y” + y’ – 4x < 0
=1đ
y’= 3x2 – 6x, y” = 6x – 6 
0,25đ
y” + y’ – 4x < 0 
0,25đ
3x2 – 4x – 6 < 0
0,25đ
0,25đ
b)Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ y0 = 2
=1đ
Pt tiếp tuyến có dạng: y = y’(x0)( x – x0) + y0
y0 = 2 
0,25đ
 tiếp điểm A(0; 2), B(3; 2)
y’= 3x2 – 6x y’(0) = 0, y’(3) = 9
0,25đ
Tiếp tuyến tại A: y = 2
0,25đ
Tiếp tuyến tại B : y = 9x – 25 
0,25đ
=3đ
Chứng minh (SBC)(SAB)
	=1đ
SA(ABC) SABC
0,25đ
 ABBC (gt)
0,25đ
BC(SAB)
0,25đ
Mà nên (SBC)(SAB)
0,25đ
Chứng minh AM(SBC)
	=1đ
ABC vuông tại B: 
0,25đ
Xét SAB vuông tại A : SA = AB= 
Nên SAB vuông cân tại A, 
0,25đ
AM là trung tuyến vừa là đường cao nên AMSB
0,25đ
Mà (SAB) (SBC) và AM(SBC)
0,25đ
c) Tính diện tích tam giác AMC
	=1đ
SAB vuông cân tại A SB = 
0,25đ
MBC vuông tại B có , BC = a
0,25đ
CM2 = BM2 + CB2 = 
0,25đ
0,25đ