Đề kiểm tra học ki I môn Toán lớp 8 có đáp án - Đề 2

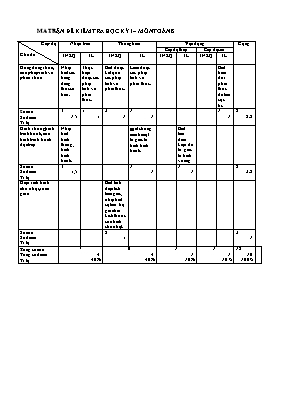
	MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I – MƠN TỐN 8
Cấp độ
Chủ đề
Nhận biết
Thơng hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Hằng đẳng thức, các phép tính về phân thức
Nhận biết các hằng đẳng thức cơ bản.
Thực hiện được các phép tính về phân thức.
Biết được kết quả các phép tính về phân thức.
Làm được các phép tính về phân thức.
Biết biến đổi phân thức để tìm cực tri.
Số câu
Số điểm
Tỉ lệ
3
1,5
1
1
2
1
1
1
1
1
8
5,5
Hình thang, hình bình hành, các hình bình hành đặc biệt
Nhận biết hình thang, hình bình hành.
Biết chứng minh một tứ giác là hình bình hành. 
Biết tìm điều kiện để tứ giác là hình vuơng
Số câu
Số điểm
Tỉ lệ
3
1,5
1
1
1
1
5
3,5
Diện tích hình chữ nhật, tam giác
Biết tính diện tích tam giác, nhận biết sự liên hệ giữa hai kích thước của hình chữ nhật.
Số câu
Số điểm
Tỉ lệ
2
1
2
1
Tổng số câu
Tổng số điểm
Tỉ lệ
7
4
40%
6
4
40%
1
1
10%
1
1
10%
15
10
100%
ĐÁP ÁN – BIỂU ĐIỂM ĐỀ KIỂM TRA HỌC KỲ 1 - 	MÔN TOÁN 8
I. TRẮC NGHIỆM (5 điểm)
Câu 1 (2 điểm). Điền dấu “X” thích hợp, mỗi kết quả đúng được 0,5 điểm
1. Sai 	2. Đúng 	3. Đúng 	4. Sai 
Câu 2 (3 điểm). Khoanh tròn vào nột chữ cái in hoa ở đầu câu trả lời đúng nhất, mỗi kết quả đúng được 0,5 điểm
1. B	2. D	3. D	4. C	5. A	6. C
II. TỰ LUẬN (5 điểm)
Bài 1 (2 điểm). Thực hiện các phép tính:
a) Thực hiện phép chia và rút gọn đúng kết quả: 	(1 điểm)
b) Thực hiện phép tính trong ngoặc được: 	(0,5 điểm)
Thay vào và tính đúng kết quả: - x	(0,5 điểm)
Bài 2 (2 điểm).
Vẽ hình đúng được 	(0,25 điểm)
	a) Sử dụng tính chất đường trung bình của tam giác để suy ra:
MN // BC và MN = BC, QP // BC và QP = BC (0,5 điểm)
Chỉ ra MN // QP và MN = QP và kết luận tứ giác 
MNPQ là hình bình hành.	(0,5 điểm)
b) Nêu được để hình bình hành MNPQ trở thành 
hình vuông thì MN = MQ và = 900 
(MN ^ MQ).	(0,5 điểm)
Sử dụng tính chất đường trung bình của tam giác 
để suy ra AD = BC và AD ^ BC.	
Kết luận: Để tứ giác MNPQ là hình vuông thì tứ giác 
ABCD phải có AD = BC và AD ^ BC.	(0,25 điểm)
Bài 3 (1 điểm).
A = = 
Tiếp tục biến đổi để biểu thức A được kết quả A = 	(0,5 điểm)
Nhận xét được: A = ³ 
Suy ra dấu “=” xảy ra khi và chỉ khi x – 2011 = 0 Û x = 2011.
Kết luận được: Khi x = 2011 thì biểu thức A đạt giá trị nhỏ nhất là: 	(0,5 điểm)
*) Ghi chú: Các cách giải khác đúng, chính xác được ghi điểm tối đa cho mỗi câu.
TRƯỜNG THCS 
Họ tên: 	
Lớp:	
KIỂM TRA HỌC KỲ 1 –MÔN TOÁN 8 Thời gian: 90 phút
Ngày:	 tháng	năm	
Mã phách
CHỮ KÝ GIÁM THỊ 1
CHỮ KÝ GIÁM THỊ 2
"
Điểm bằng số
Điểm bằng chữ
Chữ ký GK1
Chữ ký GK2
Mã phách
ĐỀ
I. TRẮC NGHIỆM (5 điểm) – Mỗi câu 0,5 điểm
Câu 1 (2 điểm). Điền dấu “X” thích hợp vào ô Đúng hoặc Sai tương ứng với mỗi phát biểu sau:
Nội dung
Đúng
Sai
1. (x – y)3 = (y – x)3
2. Phép chia đa thức 6x3 – 17x2 + 11x – 2 cho đa thức 6x2 – 5x + 1 có thương là x – 2.
3. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
4. Nếu chiều dài và chiều rộng của một hình chữ nhật tăng lên 4 lần thì diện thì diện tích hình chữ nhật tăng lên 8 lần.
Câu 2 (3 điểm). Mỗi câu 0,5 điểm. Khoanh tròn vào một chữ cái in hoa ở đầu câu trả lời đúng nhất:
1. Kết quả của phép nhân 3x2y(2x3y2 – 5xy + 1) bằng:
A. 6x5y3 + 15x3y2 + 3x2y 	B. 6x5y3 – 15x3y2 + 3x2y 	C. 6x5y3 – 5xy + 1 	D. Kết quả khác
2. Giá trị của biểu thức x2 – 5x + xy – 5y tại x = 2010; y = - 2011 bằng:
A. 2015 	B. – 2015	C. 2005	D. – 2005
3. Giá trị x thỏa mãn x2 + 6x + 9 = 0 là:
A. x = 6	B. x = - 6	C. x = 3	D. x = - 3
4. Đa thức M trong đẳng thức là:
A. 3x2 – 5	B. 3x2 + 5	C. 3x2 – 15x 	D. 3x2 + 15x
5. Cho hình thang ABCD (AB // CD) có = 1000 thì:
A. = 800	B. = 1000	C. = 800	D. = 1000
6. Cho tam giác MNQ vuông tại M, có MN = 8cm, NQ = 10cm. Diện tích của tam giác vuông MNQ bằng:
A. 48cm2	B. 40cm2	C. 24cm2	D. 12cm2
II. TỰ LUẬN (5 điểm)
Bài 1 (2 điểm). Thực hiện các phép tính sau:
a) ; 	b) 
Bài 2 (2 điểm). Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, AC, CD, DB.
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình vuông?
Bài 3 (1 điểm). Cho biểu thức A = với x > 0.
Tìm giá trị của x để biểu thức A đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Bài làm: