Đề kiểm tra học kì I môn Toán 10 - Ban cơ bản

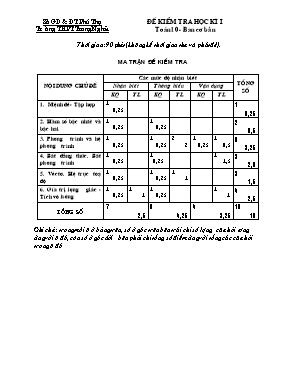
Sở GD & ĐT Phú Thọ 
Trường THPT Trung Nghĩa
Đề kiểm tra Học kì i
Toán 10 - Ban cơ bản
Thời gian: 90phút (không kể thời gian thu và phát đề).
ma trận đề kiểm tra
Nội dung chủ đề
Các mức độ nhận biết
Tổng số
Nhận biết
Thông hiểu
Vận dụng
KQ
TL
KQ
TL
KQ
TL
1. Mệnh đề- Tập hợp
1 
 0,25
1
 0,25
2. Hàm số bậc nhất và bậc hai 
1 
 0,25
1 
 0,25
2
 0,5
3. Phương trình và hệ phương trình 
1 
 0,25
1 
 0,25
2
2
1 
 0,25
1
0,5
6
3,25
4. Bất đẳng thức. Bất phương trình 
1 
 0,25
1 
 0,25
1
1,5
3
2,0
5. Véctơ. Hệ trục toạ độ
1 
 0,25
1 
 0,25
1
1
3
1,5
6. Gía trị lượng giác - Tích vô hướng
1 
 0,25
1
1
1 
 0,25
1
1
4
2,5
Tổng số
7
2,5
8
4,25
4
3,25
19
10
Ghi chú: trong mỗi ô ở bảng trên, số ở góc trên bên trái chỉ số lượng câu hỏi tương ứng với ô đó, còn số ở góc dưới bên phải chí tổng số điểm ứng với tổng các câu hỏi trong ô đó
Sở GD & ĐT Phú Thọ 
Trường THPT Trung Nghĩa
Đề kiểm tra Học kì i
Toán 10 - Ban cơ bản
Thời gian: 90phút (không kể thời gian thu và phát đề).
Phần A-Trắc nghiệm khách quan: (3 điểm)
	Chọn phương án đúng trong các câu sau .
Câu 1: Cho mệnh đề R: x2 - 4x + 5 > 0.Mệnh đề phủ định của mệnh đề trên là
 A. R: x2 - 4x + 5 > 0. B. R: x2 - 4x + 5 < 0.
 C. R: x2 - 4x + 5 0. D. R: x2 - 4x + 5 0.
Câu 2: Hai đường thẳng có phương trình tương ứng là y=3x+7 và y=mx+n song song với nhau nếu
 A. m = 3. B. n = 3 và m 7.
 C. m = 7 và n3. D. m = 3 và n 7.
Câu 3: Hàm số y=x2+2007x-2008 có đồ thị là 
A. Một đường thẳng.
B. Một parabol quay bề lõm lên phía trên.
C. Một parabol đi qua gốc toạ độ.	
D. Một parabol quay bề lõm xuống phía dưới 
Câu 4: Cặp phương trình không tương đương là 
A. và x2 + 1 = 
B. và x2 + 1 = 
C. x2(x2 + 1) = 2x2+ 2 và x2 = 2.
D. và x2 - 3x + 2 = 0.
Câu 5: Hệ phương trình có nghiệm duy nhất là 
 A. B. 
 C. D. 
Câu 6: Để được một hệ phương trình có vô số nghiệm, phương trình 2x + y = 1 
có thể kết hợp với phương trình 
 A. 2y = 4 - 4x. B. 2y = 1 - x.
 C. 2y = 2 - 4x. D. y = 2x - 1.
Câu 7: Cho tứ giác ABCD, số vectơ (khác vectơ không) mà điểm đầu và điểm cuối lấy trong số các điểm là đỉnh của tứ giác đã cho là
 A. 6 B. 12 C. 18 D. 24
Câu 8: Cho hình chữ nhật MNPQ với O là giao điểm của hai đường chéo. Trong các vectơ dưới đây, vectơ nào là vectơ đối của vectơ 
 A. B. C. D. 
Câu 9 : Cho tam giác ABC vuông tại A có góc . Số đo góc giữa hai vectơ và là 
 A. B. C. D. 
Câu 10: Cho các véctơ = (2; 3), = (1; -3). Khi đó
A. . = 0	B. . = 7 	
C. . = -11	 	D. . = -7 	
Phần B. Tự luận: (7 điểm)
Câu 1: (2,5 điểm)
1/Cho phương trình .
a/Giải phương trình với m = 3
b/Chứng minh rằng phương trình luôn có hai nghiệm phân biệt?
c/
2/Giải hệ phương trình 
Câu 2: (1,5 điểm).
Câu 3: (3 điểm). 
Trong mặt phẳng toạ độ Oxy cho tam giác ABC có các đỉnh A(2; 4), B(1; 2), C(6; 2)
a/Tính toạ độ vectơ .
b/Tính chu vi tam giác và diện tích tam giác đó.
c/Tìm toạ độ trực tâm H của tam giác ABC.
Đáp án và thang điểm
Phần I. Trắc nghiệm tự luận
	Mỗi câu trả lời đúng được 0,25 đ
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
Câu 11
Câu 12
C
D
B
A
B
C
B
B
C
D
D
C
Phần II. Trắc nghiệm tự luận
Câu 1: 
1/
a/	Với m = 3 ta có pt x2 -4x + 3 = 0 (0,5 đ)
	Giải pt tìm được nghiệm x = 1 và x = 3 (0,5 đ)
b/	Tính được = (m -1)2 - (m2 -2m) = 1 
 > 0 m nên phương trình luôn có hai nghiệm phân biệt (0,5 đ) 
2/
	 (0,5 đ)
Lấy từng vế của phương trình (1) cộng với từng vế của phương trình (2) ta được 11x = 11 tìm được x = 1
	Thay x = 1 vào phương trình (1) ta được y = -2
	Kết luận nghiệm của hệ phương trình là (x; y) = (1; -2) (0,5 đ)
Câu 2:
Ta có 
	a2 + b2 + c2 + 2ab + 2bc + 2ca 3ab + 3bc + 3ca (0,5 đ)
	 a2 + b2 + c2 - ab - bc - ca 0 (0,5 đ) 
	[(a - b)2 + (b - c)2 + (c - a)2] 0 đpcm (0,5 đ)
Câu 3:
a/	 Tính được = (-1; -2), = (4; -2), = (5; 0)	 (0, 5 đ)
b/ 	AB = = 
AC = = 2
	BC = 5 
	Chu vi của tam giác là AB + AB + BC = 5 + 3 	(0,5 đ)
	Thấy . = 0 nêm AB vuông góc với AC, tam giác ABC vuông tại A
	Diệm tích tam giác ABC là AB.AC = .2 = 5 (đvdt) (0,5 đ)
c/Do tam giác vuông tại A nên A chính là trực tâm tam giác
	 Do đó H(2; 4)	 (1 đ) 
Hết