Đề kiểm tra học kì 1 lớp 11 năm học: 2011 – 2012 môn Toán - Trường thpt chuyên Lê Quý Đôn

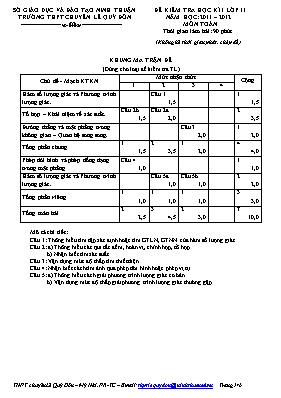
SỞ GIÁO DỤC VÀ ĐÀO TẠO NINH THUẬN	 ĐỀ KIỂM TRA HỌC KÌ 1 LỚP 11
 TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN	 	NĂM HỌC: 2011 – 2012. 
 --------------------&œ--------------------	 	MÔN TOÁN 
 Thời gian làm bài: 90 phút
 (Không kể thời gian phát, chép đề)
KHUNG MA TRẬN ĐỀ
 (Dùng cho loại đề kiểm tra TL)
Chủ đề - Mạch KTKN
Mức nhận thức
Cộng
1
2
3
4
Hàm số lượng giác và Phương trình lượng giác.
Câu 1
1,5
1
1,5
Tổ hợp – Khái niệm về xác suất.
Câu 2b
1,5
Câu 2a
2,0
2
3,5
Đường thẳng và mặt phẳng trong không gian – Quan hệ song song.
Câu 3
2,0
1
2,0
Tổng phần chung
1
1,5
2
3,5
1
2,0
4
4,0
Phép dời hình và phép đồng dạng trong mặt phẳng
Câu 4
1,0
1
1,0
Hàm số lượng giác và Phương trình lượng giác.
Câu 5a
1,0
Câu 5b
1,0
2
2,0
Tổng phần riêng
1
1,0
1
1,0
1
1,0
3
3,0
Tổng toàn bài
2
2,5
3
4,5
2
3,0
7
10,0
	Mô tả chi tiết:
	Câu 1: Thông hiểu tìm tập xác định hoặc tìm GTLN, GTNN của hàm số lượng giác 
	Câu 2: a) Thông hiểu các qui tắc đếm, hoán vị, chỉnh hợp, tổ hợp.	
	b) Nhận biết tìm xác suất.
Câu 3: Vận dụng mức độ thấp tìm thiết diện.
Câu 4: Nhận biết cách tìm ảnh qua phép dời hình hoặc phép vị tự.
Câu 5: a) Thông hiểu cách giải phương trình lượng giác cơ bản..
	b) Vận dụng mức độ thấp giải phương trình lượng giác thường gặp.
SỞ GIÁO DỤC VÀ ĐÀO TẠO NINH THUẬN	 ĐỀ KIỂM TRA HỌC KÌ 1 LỚP 11.
 TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN	 	NĂM HỌC: 2011 – 2012. 
 --------------------&œ--------------------	 	MÔN TOÁN. 
 ĐỀ CHÍNH THỨC . 	 Thời gian làm bài: 90 phút.
 (Không kể thời gian phát, chép đề).
ĐỀ:
(Đề kiểm tra có 1 trang).
A/ PHẦN CHUNG DÀNH CHO TẤT CẢ THÍ SINH: (7,0Đ).
Câu 1: (1,5 điểm) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: . 
Câu 2: a) (2,0 điểm) Tìm số hạng chứa trong khai triển của , biết tổng ba hệ số đầu tiên của khai triển bằng 79.
	b) (1,5 điểm) Từ 4 hoa hồng vàng, 5 hoa hồng nhung và 6 hoa hồng trắng, người ta chọn ngẫu nhiên 4 bông hoa để tạo thành một bó. Tính xác suất để chọn được một bó hoa tươi thắm, biết rằng một bó hoa tươi thắm phải có đủ ba màu.
Câu 3: (2,0 điểm) Cho hình chóp tứ giác S.ABCD và M, N, P lần lượt là trung điểm của AB, SA, SD. Tìm thiết diện của hình chóp cắt bởi mặt phẳng (MNP). 
B/ PHẦN RIÊNG: (3,0Đ).
 I/ CHƯƠNG TRÌNH CHUẨN: (Dành cho các lớp 11L, 11H, 11Sinh, 11Tin, 11V, 11TA).
Câu 4: (1,0 điểm) Trong mặt phẳng tọa độ Oxy cho đường thẳng . Viết phương trình đường thẳng là ảnh của đường thẳngqua phép vị tự tâm O tỉ số .
Câu 5: (2,0 điểm) Giải các phương trình: 
.	b) .
 II/ CHƯƠNG TRÌNH NÂNG CAO: (Dành cho các lớp 11A1, 11A2). 
Câu 4: (1,0 điểm) Trong mặt phẳng tọa độ Oxy cho đường thẳng . Viết phương trình đường thẳng là ảnh của đường thẳng qua phép quay tâm O góc 
Câu 5: (2,0 điểm) Giải các phương trình: 
.	b) .
 III/ CHƯƠNG TRÌNH CHUYÊN: (Dành cho lớp 11Toán).
Câu 4: (1,0 điểm) Trong mặt phẳng tọa độ Oxy cho đường tròn và đường thẳng .Viết phương trình đường trònlà ảnh của đường tròn qua phép đối xứng trục d.
Câu 5: (2,0 điểm) Giải các phương trình: 
.	b) .
--------------------------------------------------HẾT--------------------------------------------------
(Thí sinh không được sử dụng tài liệu, giám thị không giải thích gì thêm).
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ 1 LỚP 11 – MÔN TOÁN. NĂM HỌC: 2011-2012.
ĐÁP ÁN
Điểm
PHẦN CHUNG: (7 ĐIỂM)
Câu 1: Ta có: 
 Do: 
 Vậy giá trị lớn nhất của y là 4 đạt được tại ;
 giá trị nhỏ nhất của y là 0 đạt được tại ;
0,5
0,5
0,5
Câu 2: a) Tổng ba hệ số đầu trong khai triển bằng 79, ta có:
 Với ta có khai triển là: .
Theo đề bài suy ra: 
Do đó số hạng chứa là: 
b) Chọn 4 bông hoa trong 15 bông hoa, ta có: 
 Gọi A: “chọn được 4 bông hoa đủ ba màu”, ta có: 
 Vậy 
1,0
1,0
0,25
1,0
0,25
Câu 3: Hai mặt phẳng (MNP) và (ABCD) có điểm chung M và lần lượt chứa hai đường thẳng NP và AD song song nên giao tuyến của chúng là đường thẳng d qua M song song với AD.
P
D
Q
C
B
M
A
N
S
N
P
D
C
B
M
A
S
F
E
I
Trường hợp 1: Giao tuyến d cắt CD tại Q. 
Ta có:
Ta được thiết diện là hình thang MNPQ.
Trường hợp 2: Giao tuyến d cắt BC tại F.
Trong (ABCD) gọi I là giao điểm của CD và MF.
Trong (SCD) gọi E là giao điểm của IP và SC. 
Ta có:
Ta được thiết diện là ngũ giác MNPEF.
H.vẽ: 0,25
+0,25
Th1:
0,75
TH2:
0,75
PHẦN RIÊNG: (3 ĐIỂM)
 I/ CHƯƠNG TRÌNH CHUẨN: (Dành cho các lớp 11L, 11H, 11Sinh, 11Tin, 11V, 11TA).
Câu 4: Trong mặt phẳng tọa độ Oxy, nếu , giả sử và 
 thì: và 
 Ta có: .
 Vậy phương trình đường thẳng là ảnh của đường thẳng qua phép phép vị tự tâm O tỉ số 
 là: 
0,25
0,5
0,25
Câu 5: a) .	
 Vậy phương trình có nghiệm là: và với .
 b) 
 Vậy phương trình có nghiệm là: và với .
0,25
0,5
0,25
0,25
0,5
0,25
 II/ CHƯƠNG TRÌNH NÂNG CAO: (Dành cho các lớp 11A1, 11A2). 
Câu 4: Trong mặt phẳng tọa độ Oxy, nếu , giả sử và 
 thì: và 
 Ta có: .
 Vậy phương trình đường thẳng là ảnh của đường thẳng qua phép quay tâm O góc 
 là: 
0,25
0,5
0,25
Câu 5: a) 
 Vì họ nghiệm chứa trong họ nghiệm khi nên nghiệm của 
 phương trình là: .
b) 
 Vậy phương trình có nghiệm là: và với.
0,25
0,5
0,25
0,25
0,5
0,25
III/ CHƯƠNG TRÌNH CHUYÊN: (Dành cho lớp 11Toán).
Câu 4: Đường tròn có tâm và bán kính .
 Phép đối xứng trục 
 Phương trình đường trònlà ảnh của đường tròn qua phép đối xứng trục d là:
0,75
0,25
Câu 5: a) Điều kiện 
(1) 
Xét (2): ta có 
Xét (3): . 
 Vậy nghiệm của (1) là (thỏa điều kiện)
b) 
 Đặt và ta được: 
 Vậy nghiệm của phương trình là: và với 
0,5
0,5
0,5
0,5