Đề kiểm tra học kì 1 - Lớp 10 năm học: 2015- 2016 môn: Toán

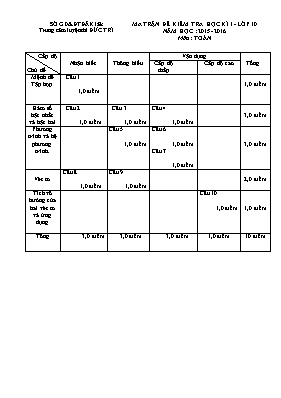
SỞ GD&ĐT ĐĂK lăk
Trung tâm luyện thi ĐỨC TRÍ
MA TRẬN ĐỀ KIỂM TRA HỌC KÌ I - LỚP 10
NĂM HỌC : 2015- 2016
Môn: TOÁN 
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp độ thấp
Cấp độ cao
Mệnh đề Tập hợp
 Câu 1
 1,0 điểm 
1,0 điểm
Hàm số bậc nhất và bậc hai
 Câu 2
 1,0 điểm 
 Câu 3
 1,0 điểm 
Câu 4
 1,0 điểm 
3,0 điểm
Phương trình và hệ phương trình.
Câu 5
 1,0 điểm 
Câu 6
 1,0 điểm 
Câu 7
 1,0 điểm 
3,0 điểm
Véc tơ
Câu 8
 1,0 điểm 
Câu 9
 1,0 điểm 
2,0 điểm
Tích vô hướng của hai véc tơ và ứng dụng 
Câu 10
 1,0 điểm 
1,0 điểm
Tổng 
 3,0 điểm 
 3,0 điểm 
 3,0 điểm 
1,0 điểm 
10 điểm
SỞ GD&ĐT ĐĂK lăk
Trung tâm luyện thi ĐỨC TRÍ
ĐỀ KIỂM TRA HỌC KÌ I- LỚP 10
NĂM HỌC : 2015- 2016
Môn: TOÁN 
Thời gian : 90 PHÚT
(Đề gồm 10 câu, 01 trang)
ĐỀ 1
Câu 1 .(1điểm) Cho các tập hợp A = (-4; 1), B = [-2; 2].Xác định các tập hợp; 
Câu 2.(1điểm) Tìm tập xác định của hàm số sau 
Câu 3. ( 1điểm )Viết phương trình đường thẳng song song với đường thẳng y = 2x - 1 và đi qua điểm 
Câu 4 .(1điểm) Vẽ đồ thị hàm số y = x2 +2x – 3. 
Câu 5 .(1điểm) Giải phương trình sau: .
Câu 6. ( 1 điểm )Giải hệ phương trình :
Câu 7.( 1 điểm )Cho phương trình x2 +2x – m = 0. (1)
Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn += 3m.
Câu 8. ( 1 điểm )Cho hình bình hành ABCD. Chứng minh rằng: 
C©u 9. (1điểm) Trong mp Oxy ,cho tam giác ABC có.
Tìm tọa độ điểm D sao cho tam giác ABD nhận C làm trọng tâm.
Câu 10 .(1điểm) .Cho biết tan . Tính giá trị của biểu thức :
.HẾT 
Ghi chú : Giám thị coi thi không giải thích gì thêm
 SỞ GD&ĐT ĐĂK lăk
Trung tâm luyện thi ĐỨC TRÍ
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA HK I LỚP 10
NĂM HỌC : 2015- 2016
Môn: TOÁN 
(Hướng dẫn chấm gồm 03 trang) 
ĐỀ 1
CÂU
ĐÁP ÁN
ĐIỂM
1 
(1,0điểm)
= [-2;1) ;
=(-4;2]
0,5đ
0,5đ
2
(1,0điểm)
y xác định 3-2x 0 x ; 
TXĐ : D = 
0,5đ
0,5đ
3
(1,0điểm)
Gọi phương trình đường thẳng có dạng 
 // y = 2x-1 nên a = 2 . Do đó (d) : y = 2x+b 
(d) đi qua nên ta có: 2.(-1) +b = 2 b=4 
Vậy (d) : y = 2x+ 4 
0,5đ
0,5đ
4
(1,0điểm)
Vẽ đồ thị hàm số y = x2 +2x – 3
Đỉnh I(-1;-4)
Trục đối xứng x= -1
Bề lõm: a =1 nên (P) có bề lõm hướng lên trên
Giao điểm với Ox: (1;0) và (-3;0)
Giao điểm với Oy: (0;-3) 
1,0 đ
5 (1,0 điểm)
 Giải phương trình : 
 (1) ĐK : 
Bình phương hai vế của (1 ) ta được
Thử lại suy ra phương trình có nghiệm x = 4
 0,5đ
0,5đ
6 (1,0 điểm)
Giải hệ phương trình : (1)
Đặt 
Hệ (1) 
Trả biến : x = 
0,5đ
0,5đ
7 (1,0 điểm)
Phương trình có hai nghiệm phân biệt
 (2)
Theo định lý Viet ta có : 
Suy ra: += 3m
Vậy m = 4 thỏa mãn yêu cầu bài toán
0,5đ
0,5đ
8 (1,0 điểm)
Vì ABCD là hình bình hành nên 
 ( quy tắc hbh)
Do đó : 
1,0 đ
9(1,0 điểm)
Cho tam giác ABC có.
Ta có: tam giác ABD nhận C làm trọng tâm nên ta có
Vậy D(2;8)
1,0đ
10
(1,0 điểm)
Ta có tan nên sin
1,0 đ
Chú ý: Học sinh giải cách khác đúng thì cho điểm tối đa
..HẾT.
SỞ GD&ĐT ĐĂK lăk
Trung tâm luyện thi ĐỨC TRÍ
ĐỀ KIỂM TRA HỌC KÌ I- LỚP 10
NĂM HỌC : 2015- 2016
Môn: TOÁN 
Thời gian : 90 PHÚT
(Đề gồm 10 câu, 01 trang)
ĐỀ 2
Câu 1 .(1điểm) Cho các tập hợp A = ( -3 ; 1) ; B = [0 ; 2 ] Xác định các tập hợp; 
Câu 2.(1điểm) Tìm tập xác định của hàm số sau 
Câu 3. ( 1điểm )Viết phương trình đường thẳng song song với đường thẳng y = 3x + 1 và đi qua điểm 
Câu 4 .(1điểm) Vẽ đồ thị hàm số y = – x2 + 4x – 3. 
Câu 5 .(1điểm) Giải phương trình sau: .
Câu 6. ( 1 điểm )Giải hệ phương trình :
Câu 7.( 1 điểm )Cho phương trình x2 +4x + m = 0. 
Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn += 3m.
Câu 8. ( 1 điểm )Gọi O là giao điểm của 2 đường chéo của hình bình hành ABCD. Chứng minh rằng: 
C©u 9. (1điểm) Trong mp Oxy ,cho tam giác ABC có
Tìm tọa độ điểm D sao cho A là trọng tâm tam giác BCD.
Câu 10 .(1điểm) .Cho biết sin . Tính giá trị của biểu thức :
.HẾT 
Ghi chú : Giám thị coi thi không giải thích gì thêm
 SỞ GD&ĐT ĐĂK lăk
Trung tâm luyện thi ĐỨC TRÍ
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA HK I LỚP 10
NĂM HỌC : 2015- 2016
Môn: TOÁN 
(Hướng dẫn chấm gồm 03 trang) 
ĐỀ 2
CÂU
ĐÁP ÁN
ĐIỂM
1 
(1,0điểm)
= [0;1) ;
=(-3;2]
0,5đ
0,5đ
2
(1,0điểm)
y xác định 1-2x 0 x ; 
TXĐ : D = 
0,5đ
0,5đ
3
(1,0điểm)
Gọi phương trình đường thẳng có dạng 
 // y = 3x+1 nên a = 3 . Do đó (d) : y = 3x+b 
(d) đi qua nên ta có: 2.1 +b = 6 b=4 
Vậy (d) : y = 3x+ 4 
0,5đ
0,5đ
4
(1,0điểm)
Vẽ đồ thị hàm số y = – x2 + 4x – 3. . 
Đỉnh I(2 ; 1)
Trục đối xứng x = 2
Bề lõm: a = - 1< 0 nên (P) có bề lõm hướng xuống dưới.
Giao điểm với Ox: (1;0) và (3;0)
Giao điểm với Oy: (0;-3)
1,0 đ
5 (1,0 điểm)
Giải phương trình :
 (2) ĐK : 
Bình phương hai vế của (2) ta được
Thử lại suy ra phương trình có hai nghiệm x = 0 và x = 1.
 0,5đ
0,5đ
6 (1,0 điểm)
Giải hệ phương trình : (1)
1,0đ
7 (1,0 điểm)
Phương trình có hai nghiệm phân biệt
 (2)
Theo định lý Viet ta có
Suy ra
Vậy thỏa mãn yêu cầu của bài toán.
0,5đ
0,5đ
8 (1,0 điểm)
Vì ABCD là hình bình hành nên giao điểm O của 2 đường chéo lần lượt là trung điểm mỗi đường 
Do đó 
1,0 đ
9(1,0 điểm)
Cho tam giác ABC với 
Ta có: tam giác BCD nhận A làm trọng tâm nên ta có
Vậy D(6;2)
1,0đ
10
(1,0 điểm)
Ta có : 
= 
1,0 đ
Chú ý: Học sinh giải cách khác đúng thì cho điểm tối đa
..HẾT.