Đề kiểm tra giữa học kỳ I môn Toán Lớp 12 (Có đáp án)

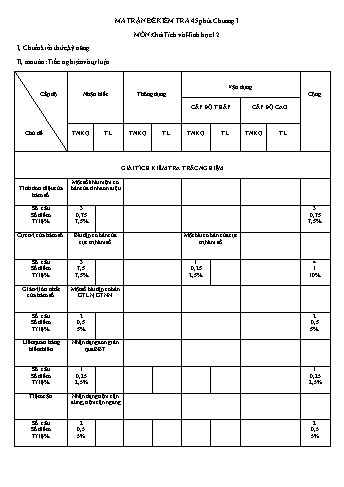
MA TRẬN ĐỀ KIỂM TRA 45 phút Chương I
MÔN:Giải Tích và Hình học 12
I, Chuẩn kiến thức,kỹ năng
II, ma trân: Trắc nghiệm và tự luận
 Cấp độ
 Chủ đề
Nhận biết
Thông dụng
Vận dụng
Cộng
CẤP ĐỘ THẤP
CẤP ĐỘ CAO
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
GIẢI TÍCH KIỂM TRA TRẮC NGHIỆM
Tính đơn điệu của hàm số
Một số khái niệm cơ bản của tính đơn điệu
Số câu
Số điểm
Tỉ lệ %
3
0,75
7,5%
3
0,75
7,5%
Cực trị của hàm số 
Bài tập cơ bản của cực trị hàm số
Một bài cơ bản của cực trị hàm số
Số câu
Số điểm
Tỉ lệ %
3
7,5
7,5%
1
0,25
2,5%
4
1
10%
Giá trị lớn nhất của hàm số
Một số bài tập cơ bản 
GTLN, GTNN
Số câu
Số điểm
Tỉ lệ %
2
0,5
5%
2
0,5
5%
Liên quan bảng biến thiên
Nhận dạng đơn giản qua BBT 
Số câu
Số điểm
Tỉ lệ %
1
0,25
2,5%
1
0,25
2,5%
Tiệm cận
Nhận dạng tiệm cận đứng, tiệm cận ngang
Số câu
Số điểm
Tỉ lệ %
2
0,5
5%
2
0,5
5%
Đồ thị hàm số
Nhận dạng thông qua đồ thị
Số câu
Số điểm
Tỉ lệ %
2
0,5
5%
2
0,5
5%
Các bài toán liên quan đến giao điẻm
Một số bài toán cơ bản liên quan đến giao điểm
Số câu
Số điểm
Tỉ lệ %
2
0,5
5%
2
0,5
5%
HÌNH THI TỰ LUẬN
Thể tích khối chóp,
Khối đa diện
Nhận biết khái niệm thể tích khối chóp
Nắm được công thức tính thể tích
Nắm chắc cách tính góc và khoảng cách, quan hệ vuông góc
Biết vận dụng thể tích vào các bài toán liên quan
Số câu
Số điểm
Tỉ lệ %
1
1,5
15%
1
1,5
15%
1
1,5
15%
1
1,5
15%
4
6,0
60%
Tổng Số câu
Tổng Số điểm
Tỉ lệ %
15
3,5
37,5%
1
1,5
15%
1
1,5
15%
1
0,25
2,5%
1
1,5
15%
1
1,5
15%
20
10,0
100%
ĐỀ KIỂM TRA GIỮA KÌ I
MÔN: Toán 12
( Thời gian: 45 phút)
I.Trắc nghiệm (4 điểm):
Câu1: Cho hàm số , kết luận nào sau đây về tính đơn điệu của hàm số là đúng:
A. Hàm số luôn nghịch biến B. Hàm số luôn đồng biến 
C. Hàm số đồng biến trên khoảng D. Hàm số đồng biến trên khoảng và nghịch biến trên khoảng 
Câu 2: Cho hàm số , kết luận nào sau đây về tính đơn điệu của hàm số là đúng:
A. Hàm số đồng biến trên B. Hàm số nghịch biến trên 
 C. Hàm số đồng biến trên các khoảng và D. Hàm số nghịch biến trên các khoảng và 
Câu 3: Trên khoảng hàm số :
A. Đồng biến B. Nghịch biến C. Cả A và B đều đúng D. Cả A và B đều sai
Câu 4: Cho hàm số . Chọn phát biểu đúng:
A. Hàm số đạt cực đại tại B. Hàm số đạt cực tiểu tại 
C. Hàm số đạt cực tiểu tại D. Cả A; B và C đều đúng
Câu 5: Cho hàm số . Chọn phát biểu đúng: 
A. Hàm số đạt cực đại tại B. Hàm số đạt cực tiểu tại 
C. Hàm số không có cực trị D. Cả A và B đều đúng
Câu 6: Cho hàm số , Chọn phát biểu đúng:
A. Đường tiệm cận đứng B. Đường tiệm cận đứng 
C. Đường tiệm cận đứng D. Đường tiệm cận đứng 
Câu7: Cho hàm số , Chọn phát biểu đúng:
 A. Đường tiệm cận ngang B. Đường tiệm cận ngang 
 C. Đường tiệm cận ngang D. Đường tiệm cận ngang 
Câu 8: Cho hàm số . Chọn phát biểu đúng:
 A. Hàm số đạt giá trị nhỏ nhất bằng -2 B. Hàm số đạt giá trị lớn nhất bằng 2 
 C. Cả A và B đều đúng D. Hàm số không tồn tại giá trị lớn nhất và giá trị nhỏ nhất.
 Câu 9: Cho hàm số . Chọn phát biểu đúng:
 A. Hàm số đạt giá trị nhỏ nhất trên bằng -1 B. Hàm số đạt giá trị lớn nhất trên bằng 4 
 C. Cả A và B đều đúng; D. Cả A và B đều sai 
Câu 10: Giá trị của m để hàm số có ba điểm cực trị là. Chọn 1 câu đúng.
A. B. C. D. 
Câu 11: Số giao điểm của đồ thị hàm số với đường thẳng là:
 A. 0; B. 1; C. 2; D. 3;
Câu 12: Với giá trị nào của tham số m thì hàm số đạt cực đại tại .
A. ; B. ; C. Cả A và B đều đúng; D. Cả A và B đều sai;
Câu 13: Với giá trị nào của tham số m thì phương trình có ba nghiệm phân biêt.
A. ; B. ; C. ; D. 
Câu 14: Đồ thị sau đây là của hàm số nào ? Chọn 1 câu đúng.
A. B. C. D. 
Câu 15. Bảng biến thiên là của hàm số nào dưới đây?
x
 2 + 
y’
 + +
y
 1 
1 
 B. C. D. 
Câu 16: Đồ thị sau đây là của hàm số nào ? Chọn 1 câu đúng
 y 
 A. B. C. D. 
II. Tự luận(6 điểm)
Đề bài: Cho khối chóp S.ABC có đường cao SA = a, đáy là tam giác vuông cân tại B, AB = BC = a. Gọi B’ là trung điểm SB, C’ là chân đường cao hạ từ A của tam giác SAC.
Tính thể tích khối chóp S.ABC 
Tính thể khối chóp S.AB’C’
Tính góc tạo bởi giữa hai mặt phẳng (SAC) và (SBC)
Tính khoảng cách từ B đến (SAC)
Đáp án
Trắc nghiệm
1.B
5.C
9.D
13.C
2.C
6.A
10.C
14.A
3.A
7.B
11.B
15.A
4.A
8.C
12.A
16.C
Tự luận
Câu
Đáp án
Điểm
Hình vẽ
a
+, Ta có: SABC = 12AB.BC= a22 
⇒ VABC=13SABC.SA= a36 
0,5
1,0
b
+, Ta có 
+, Do đó: 
Suy ra: 
0,5
0,5
0,5
c
+, Chứng minh: SC ⊥(AB'C')
Ta có : BC ⊥ AB và BC ⊥ SA => BC ⊥ (SAB) => AB’ ⊥ BC mà AB’ ⊥ SB ( do △SAB cân tại A, B'là trung điểm SB)=>AB'⊥ SBC=>SC ⊥AB'( 1)
+, Mặt khác SC ⊥ AC’ ( 2)
Nên: SC ⊥ (AB’C’)
+, góc giữa mặt phẳng (SAB) và (SBC) là góc (AC’, B’C’) = AC'B'
+, do △SAB vuông cân tại A => AB’ = 12 SB= a22
 +, Xét tam giác SAC vuông tại A => 
+, Xét tam giác vuông AB’C’ => 
+, . 
Vậy giữa hai mặt phẳng (SAB) và (SBC) là 600.
0,25
0,25
0,5
0,5
d
+, Vì ( gt), từ B kẻ BH BC = > BH (SAC), cho nên khoảng cách từ B đến mặt phẳng (SAC) là BH
+, Mặt khác, tam giác ABC vuông cân tại B => BH = AC = 
=> d(B,(SAC)) = 
0,5
0,5
0,5