Đề kiểm tra Chương I môn Giải tích Lớp 12 (Cơ bản) (Kèm đáp án)

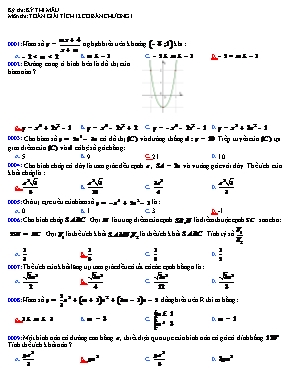
Kỳ thi: KỲ THI MẪU
Môn thi: TOÁN GIẢI TÍCH 12 CƠ BẢN CHƯƠNG 1
0001: Hàm số nghịch biến trên khoảng khi :
A. 	B. 	C. 	D. 
0002: Đường cong ở hình bên là đồ thị của hàm nào ?
A. 	B. 	C. 	D. 
0003: Cho hàm số có đồ thị và đường thẳng . Tiếp tuyến của tại giao điểm của và có hệ số góc bằng:
A. 5.	B. 9.	C. 21.	D. 10.
0004: Cho hình chóp có đáy là tam giác đều cạnh , và vuông góc với đáy. Thể tích của khối chóp là :
A. 	B. 	C. 	D. 
0005: Giá trị cực tiểu của hàm số là :
A. 0	B. 1	C. 3	D. -1
0006: Cho hình chóp . Gọi là trung điểm của cạnh là điểm thuộc cạnh sao cho: . Gọi là thể tích khối là thể tích khối . Tính tỷ số 
A. 	B. 	C. 	D. 
0007: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a là :
A. 	B. 	C. 	D. 
0008: Hàm số đồng biến trên R thì m bằng :
A. 	B. 	C. 	D. 
0009: Một hình nón có đường cao bằng , thiết diện qua trục của hình nón có góc ở đỉnh bẳng . Tính thể tích khối nón ?
A. 	B. 	C. 	D. 
0010: Đường thẳng là tiệm cận đứng của đồ thị hàm số nào ?
A. 	B. 	C. 	D. 
0011: Giá trị lớn nhất của hàm số trên đoạn 
A. 0	B. 3	C. 1	D. 2
0012: Hàm số đồng biến trên khoảng nào ?
A. và 	B. 
C. 	D. 
0013: Tìm để phương trình có 3 nghiệm phân biệt
A. .	B. .	C. .	D. .
0014: Một chất điểm chuyển động theo quy luật . Tính thời điểm t (giây) tại đó vận tốc v(m/s) đạt giá trị lớn nhất
A. 	B. 	C. 	D. 
0015: Tọa độ giao điểm của hai đồ thị và là :
A. 	B. 	C. 	D. 
0016: Tâm đối xứng của đồ thị hàm số có tọa độ là :
A. 	B. 	C. 	D. 
0017: Cho hàm số có và . Khẳng định nào sau đây đúng ?
A. Đồ thị hàm số đã cho có tiệm cận đứng là và 
B. Đồ thị hàm số đã cho không có tiệm cận đứng
C. Đồ thị hàm số đã cho có tiệm cận đứng là và 
D. Đồ thị hàm số đã cho có đúng một tiệm cận đứng
0018: Tìm để hàm số có giá trị cực đại là , giá trị cực tiểu là , thỏa mãn 
A. 	B. 	C. 	D. 
0019: Tìm để hàm số có hai điểm cưc trị , , thỏa mãn 
A. 	B. 	C. 	D. 
0020: Cho hàm số , giá trị để khoảng cách giữa hai điểm cưc trị của đồ thị hàm số trên bằng 
A. 	B. 	C. 	D.