Đề kiểm tra Chương I môn Đại số và giải tích 11

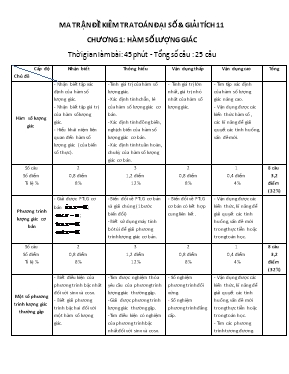
MA TRẬN ĐỀ KIỂM TRA TOÁN ĐẠI SỐ & GIẢI TÍCH 11
CHƯƠNG 1: HÀM SỐ LƯỢNG GIÁC
Thời gian làm bài: 45 phút - Tổng số câu : 25 câu
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Tổng
Hàm số lượng giác
- Nhận biết tập xác định của hàm số lượng giác.
- Nhận biết tập giá trị của hàm số lượng giác.
- Hiểu khái niệm liên quan đến hàm số lượng giác (của biến số thực). 
- Tính giá trị của hàm số lượng giác.
- Xác định tính chẵn, lẻ của hàm số lượng giác cơ bản.
- Xác định tính đồng biến, nghịch biến của hàm số lượng giác cơ bản.
- Xác định tính tuần hoàn, chu kỳ của hàm số lượng giác cơ bản.
- Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác.
- Tìm tập xác định của hàm số lượng giác nâng cao.
- Vận dụng được các kiến thức hàm số , các kĩ năng để giải quyết các tình huống, vấn đề mới.
Số câu
Số điểm
Tỉ lệ %
2
0,8 điểm
8%
3
1,2 điểm
12%
2
0,8 điểm
8%
1
0,4 điểm
4%
8 câu
3,2 điểm
(32%)
Phương trình lượng giác cơ bản
- Giải được PTLG cơ bản ; ; ;
.
- Biến đổi về PTLG cơ bản và giải chúng (1 bước biến đổi)
- Biết sử dụng máy tính bỏ túi để giải phương trình lượng giác cơ bản. 
- Biến đổi về PTLG cơ bản có kết hợp cung liên kết.
- Vận dụng được các kiến thức, kĩ năng để giải quyết các tình huống, vấn đề mới trong thực tiễn hoặc trong toán học.
Số câu
Số điểm
Tỉ lệ %
2
0,8 điểm
8%
3
1,2 điểm
12%
2
0,8 điểm
8%
1
0,4 điểm
4%
8 câu
3,2 điểm
(32%)
Một số phương trình lượng giác thường gặp
- Biết điều kiện của phương trình bậc nhất đối với sinx và cosx.
- Biết giải phương trình bậc hai đối với một hàm số lượng giác.
- Tìm được nghiệm thỏa yêu cầu của phương trình lượng giác thường gặp.
- Giải được phương trình lượng giác thường gặp.
- Tìm điều kiện có nghiệm của phương trình bậc nhất đối với sinx và cosx.
- Số nghiệm phương trình đối xứng.
- Số nghiệm phương trình đẳng cấp.
- Vận dụng được các kiến thức, kĩ năng để giải quyết các tình huống, vấn đề mới trong thực tiễn hoặc trong toán học.
- Tìm các phương trình tương đương.
Số câu
Số điểm
Tỉ lệ %
2
0,8 điểm
8%
3
1,2 điểm
12%
3
1,2 điểm
12%
1
0,4 điểm
4%
9 câu
3,6 điểm
(36%)
Tổng số câu
Tổng số điểm
Tỉ lệ %
6
2,4 điểm
24%
9
3,6 điểm
36%
7
2,8 điểm
28%
3
1,2 điểm
12%
25 câu
10 điểm
(100%)
BẢNG MÔ TẢ CHI TIẾT NỘI DUNG CÂU HỎI ĐỀ KIỂM TRA
 CHƯƠNG 1: HÀM SỐ LƯỢNG GIÁC – GIẢI TÍCH 11
 Thời gian làm bài: 45 phút – Tổng số câu: 25 câu
CHỦ
ĐỀ
CÂU
CẤP
ĐỘ
MÔ TẢ
1. Hàm
số lượng giác
1
NB
Tìm tập xác định của hàm số lượng giác cơ bản.
2
NB
Tìm tập giá trị của hàm số lượng giác cơ bản.
3
TH
Tính giá trị của hàm số lượng giác cơ bản.
4
TH
Xác định tính chẵn/lẻ của hàm số lượng giác cơ bản.
5
TH
Xác định tính đồng biến/nghịch biến của hàm số lượng giác cơ bản.
6
VDT
Tìm tập giá trị của hàm số lượng giác bất kỳ.
7
VDT
Tìm giá trị lớn nhất/ nhỏ nhất của hàm số lượng giác bất kỳ.
8
VDC
Tìm tham số m để hàm số lượng giác thỏa điều kiện cho trước.
2.
Phương
trình
lượng
giác cơ
bản
9
NB
Biết tập nghiệm của phương trình lượng giác cơ bản.
10
NB
Biết điều kiện có nghiệm của phương trình lượng giác cơ bản.
11
TH
Giải phương trình lượng giác cơ bản.
12
TH
Giải phương trình lượng giác cơ bản.
13
TH
Giải phương trình lượng giác cơ bản.
14
VDT
Biến đổi cơ bản (cung liên kết, pt tích, công thức) để giải phương
trình lượng giác cơ bản.
15
VDT
Biến đổi cơ bản (cung liên kết, pt tích, công thức) để giải phương
trình lượng giác cơ bản.
16
VDC
Ứng dụng PTLG cơ bản trong bài toán chơi đu.
3. Một
số
phƣơng
trình
lƣợng
giác
thƣờng
gặp
17
NB
Tìm điều kiện của phương trình bậc nhất đối với sinx và cosx.
18
NB
Giải phương trình bậc hai đối với một hàm số lượng giác.
19
TH
Tìm được nghiệm thỏa yêu cầu của phương trình lượng giác thường
gặp.
20
TH
Giải được phương trình lượng giác thường gặp.
21
TH
Tìm điều kiện có nghiệm của phương trình bậc nhất đối với sinx và
cosx.
22
VDT
Tìm số nghiệm phương trình đối xứng.
23
VDT
Tìm số nghiệm phương trình đẳng cấp.
24
VDT
Tìm các phương trình tương đương.
25
VDC
Ứng dụng phương trình bậc nhất đối với sin & cos để giải bài toán
vật lý.
ĐỀ KIỂM TRA TOÁN ĐẠI SỐ VÀ GIẢI TÍCH 11
CHƯƠNG 1: HÀM SỐ LƯỢNG GIÁC
Thời gian làm bài: 45 phút – Tổng số câu: 25 câu
Câu 1: Mệnh đề nào sau đây là đúng?
A. Mọi hàm số lượng giác đều có tập giá trị là .
B. Hàm số có tập giá trị là .
C. Hàm số có tập giá trị là .
D. Hàm số có tập giá trị là 
Câu 2: Hàm số nào sau đây có tập xác định là ?
A. .
B. .
C. .
D. 
Câu 3: Trên khoảng hàm số nào sau đây luôn nhận giá trị dương?
A. .
B. .
C. .
D. .
Câu 4: Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
A. .
B. .
C. .
D. .
Câu 5: Hàm số đồng biến trên khoảng?
A . 
B .
C. 
D. 
Câu 6: Tập giá trị của hàm số là tập nào sau đây?
A . 
B . 
C .
D . 
Câu 7: Giá trị lớn nhất của hàm số bằng?
A . 
B .
C .
D .
Câu 8: Tìm tất cả các giá trị tham số để hàm số có tập xác định là 
A . 
B .
C .
D .
Câu 9: Tập nghiệm của phương trình với cho trước là:
A . 
B . 
C . 
D . 
Câu 10: Nghiệm của phương trình là:
A. 
B.
C.
D.
Câu 11: Cho phương trình với là số cho trước. Mệnh đề nào sau đây là đúng?
A.Phương trình luôn có nghiệm với mọi số thực .
B. Phương trình luôn có nghiệm với mọi số thực .
C.Phương trình luôn có nghiệm với mọi số thực .
D.Phương trình luôn có nghiệm với mọi số thực .
Câu 12: Nghiệm của phương trình là:
A. 
B.
C.
D..
Câu 13:Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm 
của phương trình ?
A. cos x = -1.	
B. cos x = 1.	
C. tan x = 1 .	
D. cot x  = 0.
Câu 14: Số nghiệm của phương trình sin2x + cosx = 0 trên [-2p;2p] là :
A. 0	
B. 2	
C. 4	
D. 8.
Câu 15: Trên khoảng (0;p), phương trình tanx.tan2x = 1 
A. chỉ có các nghiệm là : . 
B. chỉ có các nghiệm là: .
C. chỉ có các nghiệm là : .
D. chỉ có các nghiệm là: .
Câu 16: Mùa xuân ở hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún đều, câu đu sẽ đưa người chơi đu dao động qua lại vị trí cân bằng. Nghiên cứu trò chơi này, người ta thấy khoảng cách h (tính bằng mét) từ người đu đến vị trí cân bằng được biểu diễn qua thời gian t ( t ³ 0 và được tính bằng giây) bởi hệ thức h = |d| với Trong đó, ta quy ước rằng d>0 khi vị trí cân bằng ở về phái sau lưng người chơi đu và d<0 trong truòng hợp ngược lại. Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu ở xa vị trí cân bằng nhất?
A.  0,5 giây và 1 giây.
B.  0,5 giây và 2 giây.
C.  1 giây và 2 giây 
D.  2 giây và 4 giây.
Câu 17: Điều kiện có nghiệm của phương trình 3sin3x + 4sin3x = C là
A. 	
B. - 5 < C < 5
C. 3 < C < 4	
D. 
Câu 18: Nghiệm của phương trình là
A. 	
B. 
C. 	
D. 
Câu 19: Nghiệm dương nhỏ nhất của phương trình sin2x = sinx là
A. 	
B. 
C. 	
D. 
Câu 20: Xét các phương trình lượng giác
	(I) sinx + cosx = 2
	(II) tanx + cotx = 2
	(III) 
Trong các phương trình trên, phương trình nào có nghiệm:
A. (I)	
B. (II)
C. (III)	
D. (II) và (III)
Câu 21: Tìm m phương trình sau có nghiệm 
A. 	
B. 	
C. 	
D. 
Câu 22: Số nghiệm của phương trình trên là 
A. 	
B. 	
C. 	
D. 
Câu 23: Số nghiệm của phương trình trên là 
A. 	
B. 	
C. 	
D. 
Câu 24: Phương trình tương đương với phương trình
A. 	
B. 	
C. 	
D. 
Câu 25: Số giờ có ánh sáng mặt trời của TPHCM trong năm 2018 được cho bởi công thức với là số ngày. Hỏi, vào ngày mấy tháng mấy trong năm (dương lịch) thì số giờ có ánh sánh mặt trời của TPHCM là gần 14h? 
A. 	
B. 	
C. 	
D.