Đề kiểm tra chương 4 môn Đại số 9

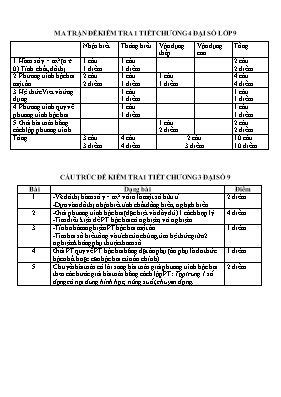
MA TRẬN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 4 ĐẠI SỐ LỚP 9
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Tổng
1. Hàm số y = ax2 (a ≠ 0). Tính chất, đồ thị. 
1 câu
1 điểm
1 câu
1 điểm
2 câu
2 điểm
2. Phương trình bậc hai một ẩn.
2 câu
2 điểm
1 câu
1 điểm
1 câu
1 điểm
4 câu
4 điểm
3. Hệ thức Viet và ứng dụng.
1 câu
1 điểm
1 câu
1 điểm
4. Phương trình quy về phương trình bậc hai.
1 câu
1 điểm
1 câu
1 điểm
5. Giải bài toán bằng cách lập phương trình.
1 câu
2 điểm
2 câu
2 điểm
Tổng
3 câu
3 điểm
4 câu
4 điểm
2 câu
3 điểm
10 câu
10 điểm
CẤU TRÚC ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3 ĐẠI SỐ 9
Bài
Dạng bài
Điểm
1
-Vẽ đồ thị hàm số y = ax2 với a là một số hữu tỉ.
-Dựa vào đồ thị nhận biết tính chất đồng biến, nghịch biến.
2 điểm
2
-Giải phương trình bậc hai (đặc biệt và đầy đủ) 1 cách hợp lý.
-Tìm điều kiện để PT bậc hai có nghiệm, vô nghiệm.
4 điểm
3
-Tính nhẩm nghiệm PT bậc hai một ẩn.
-Tìm hai số biết tổng và tích của chúng, tìm hệ thức giữa 2 nghiệm không phụ thuộc tham số.
1 điểm
4
Giải PT quy về PT bậc hai bằng đặt ẩn phụ (ẩn phụ là đa thức bậc nhất hoặc căn bậc hai của ẩn chính)
1 điểm
5
Chuyển bài toán có lời sang bài toán giải phương trình bậc hai theo các bước giải bài toán bằng cách lập PT: Tập trung 1 số dạng có nội dung hình học, năng suất, chuyển động.
2 điểm
UBND QUẬN LÊ CHÂN
TRƯỜNG THCS VÕ THỊ SÁU
ĐỀ CHÍNH THỨC
CS
ĐỀ KIỂM TRA CHƯƠNG 4
MÔN ĐẠI SỐ 9
(Thời gian làm bài: 45 phút) 
Bài 1 (2 điểm): 
Cho hàm số y = ax2 (với a ≠ 0) có đồ thị là (P).
a/ Xác định hệ số a biết (P) đi qua điểm 
b/ Với giá trị a vừa tìm được hãy cho biết hàm số đã cho đồng biến khi nào ? Nghịch biến khi nào ?
Bài 2 (6 điểm):
1/ Giải các phương trình.
2/ Cho phương trình x2 – 2 (m + 1)x + 2m = 0 (1), m là tham số.
a/ Chứng minh rằng phương trình (1) luôn có 2 nghiệm phân biệt với mọi m.
b/ Giả sử x1, x2 là 2 nghiệm của phương trình. Tìm giá trị của m biết .
c/ Tìm một hệ thức liên hệ giữa hai nghiệm độc lập đối với m.
Bài 3 (2 điểm). Bài toán thực tế. 
Theo quy định về sân bóng đá cỏ nhân tạo mini 5 người thì: “Sân hình chữ nhật, trong mọi trường hợp, kích thước chiều dọc sân phải lớn hơn kích thước chiều ngang sân. Chiều ngang tối đa là 25m và tối thiểu là 15m, chiều dọc tối đa là 42m và tối thiểu là 25m”. Thực hiện đúng quy định kích thước sân 5 người là điều quan trọng để quản lý sân bóng và việc thi đấu của các cầu thủ.
Sân bóng đá mini cỏ nhân tạo Bến Bính có chiều dọc dài hơn chiều ngang 22m, diện tích sân là 779m2. Hỏi kích thước sân này có đạt tiêu chuẩn đã quy định hay không ?
---------------Hết---------------
ĐÁP ÁN VÀ CHO ĐIỂM
Bài
Đáp án
Điểm
Bài 1
(2 điểm)
a/ Vì (P) đi qua điểm M ( ; 1) nên ta có 1 = a.Þ (TMĐK). Vậy .
0,5
0,5
b/ Vì nên hàm số đồng biến khi x > 0,
 nghịch biến khi x < 0.
0,5
0,5
Bài 2
(6 điểm)
1.
có D = 32 – 4. 2 . (-6) = 9 +48 = 57 > 0
Phương trình có 2 nghiệm phân biệt 
0,5
1,0
1. b/ 
Đặt x2 = t với t ≥ 0, ta được PT: 
có a – b + c = 1 – (-2) + (-3) = 0
Þ t1 = -1 , t2 = 3 
Giá trị t1 = -1 không TMĐK, giá trị t2 = 3 TMĐK
Với t = 3 
Vậy PT đã cho có 2 nghiệm 
0,25
0,25
0,25
0,5
0,25
 2. a/ x2 – 2(m + 1)x + 2m = 0 (1)
D’ = (m + 1)2 - 2m = m2 +1 > 0 với mọi m.
PT(1) luôn có hai nghiệm phân biệt với mọi m.
0,5
0,5
 2. b/ PT (1) có hai nghiệm x1, x2. Theo định lý Viet có .
Lại có 
Vậy .
0,25
0,25
0,25
0,25
2. c/ PT (1) có hai nghiệm x1, x2. Theo định lý Viet có 
Ta có S –P = 2 là hệ thức liên hệ giữa 2 nghiệm độc lập đối với m.
0,5
0,5
Bài 3
(2 điểm)
Gọi chiều ngang sân là x (m), điều kiện x > 0.
Suy ra chiều dọc sân bóng là x + 22 (m).
Vì sân bóng hình chữ nhật có diện tích 779m2, nên ta có phương trình: x.(x + 22 ) = 779
Giải phương trình: x. (x + 22 ) = 779
 Û x2 + 22x – 779 = 0
D’ = 112 – (-779) = 900 > 0
x1 = -11 + 30 = 19 (TMĐK)
x2 = -11 - 30 = -41 (không TMĐK)
Vậy chiều ngang sân bóng là 19m, chiều dọc sân bóng là 19 + 22 = 41m.
Kích thước này đạt tiêu chuẩn trong quy định.
0,25
0,5
0,5
0,5
0,5