Đề kiểm tra chất lượng học kỳ II toán 11

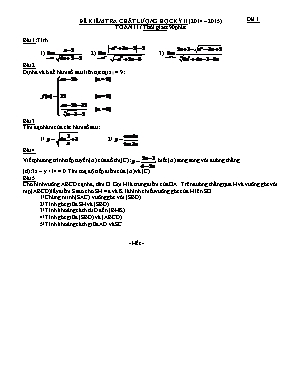
ĐỀ 1
ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KỲ II (2014 - 2015)
TOÁN 11 / Thời gian: 90phút
Bài 1:Tính 
1) 	2) 	3) 
Bài 2
Định a và b để hàm số sau liên tục tại x0 = 9:
Bài 3
Tìm đạo hàm của các hàm số sau:
1/ 	2/ 
Bài 4
Viết phương trình tiếp tuyến (Δ) của đồ thị (C):, biết (Δ) song song với đường thẳng
(d): 3x – y +14 = 0. Tìm toạ độ tiếp điểm của (Δ) và (C).
Bài 5
Cho hình vuông ABCD cạnh a, tâm O. Gọi H là trung điểm của OA. Trên đường thẳng qua H và vuông góc với mp(ABCD) lấy điểm S sao cho SH = a và K là hình chiếu vuông góc của H lên SO
	1/ Chứng minh (SAC) vuông góc với (SBD)
	2/ Tính góc giữa SH và (SBD)
 3/ Tính khoảng cách từ D đến (BHK)
	4/ Tính góc giữa (SBD) và (ABCD)
	5/ Tính khoảng cách giữa AD và SC
 - Hết -
Bài 1: 0.75đx3 
Bài 2: 1đ
Hàm số sau liên tục tại x0 = 9 
Bài 3: 0,75đx2
Bài 4 1,25
 + (Δ): 3x – y + c = 0 (c khác 14) 0,25
 + 0,25 
+ (Δ) tx (C) khi và chỉ khi hpt sau có n0 x khác 4/5:
Vậy có hai tt thoả ycbt :
(Δ1): y = 3x – 8/5 tx (C) tại A(3/5;1/5)
(Δ2): y = 3x – 4 tx (C) tại B(1;-1) 0,25
Bài 5 4đ
2/ SK là hcvg của SH lên (SBD) 0,25
=> Ð(SH,(SBD))= Ð(SH,SK) 0,25
3/ nên HK┴(SBD)
=> (BHK) (SBD) theo giao tuyến BK 
 Kẻ ON BK 
 0,25
4/ 
5/ AD//BC => AD//(SBC)
 =>d(AD,SC)=d(AD,(SBC)) 0,25
 Trong (ABCD) dựng HL//AB (LÎBC).
CM được (SHL)┴(SBC). Trong (SHL) dựng HM┴SL, SL=(SHL)ÇSBC)=> HM┴(SBC) 0,25
=>d(H,(SBC)) = HM = 3a/5 0,25
=> d(AD,SC)=d(AD,(SBC))= d(A,(SBC))
 = 4/3. d(H,(SBC))=4a/5 0,25
* Có thể tính
+ d(AD,SC)=d(AD,(SBC)) (0,25) = d(L’,(SBC)) 
+Dựng được đường vuông góc từ L’ 0,25
+Dùng ct diện tích ra kết quả 0,5	`