Đề kiểm tra 45 phút Đại số 10 - Chương IV

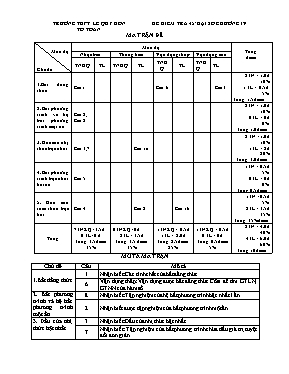
TRƯỜNG THPT LÊ QUÝ ĐÔN
TỔ TOÁN
ĐỀ KIỂM TRA 45’ ĐẠI SỐ CHƯƠNG IV
MA TRẬN ĐỀ
 Mức độ
Chủ đề 
Mức độ
Tổng
điểm
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1.Bất đẳng thức
Câu1
Câu 6
Câu3
2TN = 1.0đ
10%
 1 TL = 0.5 đ
5%
Tổng: 1.5điểm
2. Bất phương trình và hệ bất phương trình một ẩn
Câu 8, Câu 2
2TN = 1.0đ
10%
0TL = 0đ
0%
Tổng:1.0điểm
3. Dấu của nhị thức bậc nhất
Câu 3,7
Câu 1a
2 TN =1.0đ
10%
 1TL = 2đ
20%
Tổng: 3.0điểm
4. Bất phương trình bậc nhất hai ẩn
Câu 5
1TN = 0.5đ
5%
 0TL = 0đ
0%
Tổng:0.5điểm
5. Dấu của tam thức bậc hai
Câu 4
Câu 2
Câu 1b
1TN =0.5đ
5%
 2TL = 3.5đ
35%
Tổng: 35%điểm
Tổng
7TNKQ =3.5đ
0 TL=0 đ
Tổng: 3.5điểm
35%
0TNKQ =0đ
2TL = 3.5đ
Tổng: 3.5 điểm
35%
1TNKQ = 0.5đ
1TL = 2.0đ
Tổng: 2.5 điểm
25%
1TNKQ = 0.5đ
0 TL = 0đ
Tổng: 0.5điểm
5%
8TN = 4.0đ
40%
 4TL = 6.0đ
60%
Tổng: 10điểm
MÔ TẢ MA TRẬN
Chủ đề
Câu
Mô tả
1.Bất đẳng thức
1
Nhận biết: Các tính chất của bất đẳng thức
6
Vận dụng thấp: Vận dụng được bất đẳng thức Côsi để tìm GTLN, GTNN của hàm số
2. Bất phương trình và hệ bất phương trình một ẩn
8
Nhận biết: Tập nghiệm của hệ bất phương trình bậc nhất 1 ẩn
2
Nhận biết được tập nghiệm của bất phương trình một ẩn
3. Dấu của nhị thức bậc nhất
3
Nhận biết: Dấu của nhị thức bậc nhất
7
Nhận biết: Tập nghiệm của bất phương trình chứa dấu giá trị tuyệt đối đơn giản
1a (TL)
Thông hiểu: Cách giải bất phương trình chứa ẩn ở mẫu dựa vào xét dấu của nhị thức bậc nhất
4. Bất phương trình bậc nhất hai ẩn
5
Nhận biết: Miền nghiệm của bất phương trình bậc nhất hai ẩn
5. Dấu của tam thức bậc hai
4
Nhận biết: Tập nghiệm của bất phương trình bậc hai
7
Nhận biết: Dấu của tam thức bậc hai
2(TL)
Thông hiểu: Cách tìm m để bất phương trình có nghiệm đúng với mọi x thuộc 
3(TL)
Vận dụng: Vận dụng được định lí về dấu của tam thức bậc hai để giaỉ bất phương trình chứa căn là một tam thức bậc hai
ĐỀ RA
I. TRẮC NGHIỆM (4 điểm)
Câu 1. Mệnh đề nào sau đây là mệnh đề đúng
A. Với mọi số thực a, b, c ta có: ;
B. Với mọi số thực a, b ta có: ;
C. Với mọi số thực a, b, c, d ta có: a < b và c < d a +c < b+d;
D. Với mọi số thực a, b, c, d ta có: a < b và c < d ac < bd.
Câu 2. Tập nghiệm của bất phương trình là:
A. ;
B. ;
C. ;
D. .
Câu 3. Tập nghiệm của bất phương trình là:
A. ;
B. ;
C. ;
D. .
Câu 4. Tập nghiệm của bất phương trình là:
A. ;
B. ;
C. ;
D. .
Câu 5. Trong hình vẽ dưới, phần không bị gạch sọc (kể bờ) là miền nghiệm của hệ bất phương trình nào?
x
y
O
3x +2y - 6=0
4x+y-12=0
A. ;	B. ;
C. ;	D. .
Câu 6. Giá trị lớn nhất của hàm số : f(x)=(x+3)(5-x) là:
A. 4;
B. -3;
C. 1;
D. 16.
Câu 7. Nghiệm của bất phương trình là:
A. ;
B. ;
C. ;
D. .
 Câu 8: là tập nghiệm của hệ bất phương trình nào sau đây?
A. ;
B. ;
C. ;
D. .
II. TỰ LUẬN (6 điểm)
Câu 1. Giải các bất phương trình sau:
a) 	b) 
Câu 2. Cho . Tìm m để bất phương trình vô nghiệm.
Câu 3. Cho hai số thực dương x, y thỏa mãn điều kiện x + y + 1 = 3xy
Tìm GTLN của biểu thức sau: 
V. ĐÁP ÁN VÀ THANG ĐIỂM
Bài
Nội dung
Điểm
Phần trắc nghiệm
1C, 2D, 3A, 4C, 5A, 6D, 7B, 8D
4,0
Phần tự luận
Câu 1a
2,0 đ
. 
Lập bảng xét dấu f(x)
x
 0 2 3 
x
 - 0 +
+
+
x-2
-
 - 0 + 
+
x-3
-
-
 - 0 +
f(x)
 0 +
-
+
Dựa vào bảng xét dấu ta có bất phương trình đã cho có tập nghiệm là 
0.5
0.25
0.25
0.25
0.5
0.25
Câu 1b
2,0đ
Vậy bất phương trình đã cho có tập nghiệm là 
0.75
0.75 -0.25
0.25
Câu 2
1,5đ
TH1: m = 1. Bất phương trình trở thành -1 > 0.
Suy ra với m = 1 bất phương trình đã cho vô nghiệm (1)
TH2: m 1 bất phương trình đã cho vô nghiệm khi và chỉ khi 
 (2)
Từ (1) và (2) ta suy ra các giá trị của m cần tìm là 
0.5
0.5
0.25
0.25
Câu 3
0,5đ
Áp dụng bất đẳng thức Cauchy ta có: 3xy 
Áp dụng bất đẳng thức Cauchy ta có: 
, đặt 
 đồng biến trên nên đạt GTLN tại t=1
Vậy GTLN của biểu thức là 1, đạt được khi và chỉ khi x = y =1
0.25
0.25