Đề kiểm tra 45 phút - Chương III - Học kì II - Hình học 10 - Ban cơ bản

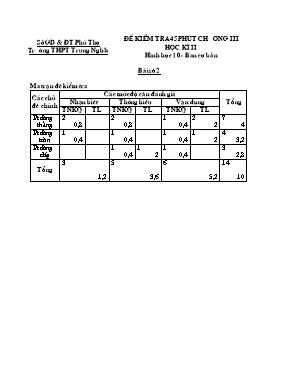
Së GD & §T Phó Thä 
Tr­êng THPT Trung NghÜa
§Ò kiÓm tra 45 phót ch­¬ng Iii 
Häc k× ii
H×nh häc 10 - Ban c¬ b¶n
Bµi sè 2
Ma trËn ®Ò kiÓm tra 
C¸c chñ ®Ò chÝnh
C¸c møc ®é cÇn ®¸nh gi¸
Tæng
NhËn biÕt
Th«ng hiÓu
VËn dông
TNKQ
TL
TNKQ
TL
TNKQ
TL
Pt ®­êng th¼ng
2
0,8
2
0,8
1
0,4
2
2
7
4
Pt ®­êng trßn
1
0,4
1
0,4
1
0,4
1
2
4
3,2
Pt ®­êng elÝp
1
0,4
1
2
1
0,4
3
2,8
Tæng
3
1,2
5
3,6
6
5,2
14
10
Së GD & §T Phó Thä 
Tr­êng THPT Trung NghÜa
§Ò kiÓm tra 45 phót ch­¬ng Iii 
Häc k× ii
H×nh häc 10 - Ban c¬ b¶n
Bµi sè 2
PhÇn I. Tr¾c nghiÖm kh¸ch quan (4 ®iÓm)
H·y chän ph­¬ng ¸n ®óng cho c¸c c©u sau .
1/ Cho đường thẳng d có pt tham số . Một vectơ chỉ phương của d có tọa độ là 
	a	(1; -2)	b	(-1; 3) 	c	(1; 2)	d	(-1; -2)
 2/ Trong các điểm sau, điểm nào nằm trên đường thẳng d có pt tham số 
	a	(1; -1)	b	(0; -2)	c	(-1; 1)	d	(1;1)
 3/ Cho pt ax + by + c = 0. Điều kiện để pt đó là pt của một đường thẳng là
	a	a + b 0	 	b	a và b phải là các số dương
	c	a2 + b2 0	d	a và b là các số nguyên
 4/ Đường thẳng đi qua điểm M(1; 2) và song song với đường thẳng d : 4x + 2y + 1 = 0 
	có pt tổng quát là :
	a	2x + y + 3 = 0	b	2x - y - 4 = 0
	c	4x + 2y + 3 = 0	d	2x + y + 4 = 0
 5/ Hình chiếu vuông góc của điểm M(1; 4) xuống đường thẳng d : x -2y + 2 = 0 
	có tọa độ là 
	a	(2; -2)	b	(2; 2)	c	(3; 0)	d	(0; 3)
6/ Pt nào trong các pt sau không là pt đường tròn
	a	x2 + y2 -4 = 0	b	x2 + y2 + x + y = 0
	c	x2 + y2 -2x -2y + 1 = 0	d	x2 + y2 + x + y + 2 = 0 
 7/ Tiếp tuyến với đường tròn (C) : x2 + y2 = 2 tại điểm M0(1; 1) có pt là :
	a	x + y + 1 = 0	b	2x + y -3 = 0
	c	x -y = 0	d	x + y -2 = 0
 8/ Cho điểm M(2; 3) nằm trên đương elíp (E) có pt chính tắc + = 1
	Trong các điểm sau đây điểm nào không nằm trên elíp (E) :
	a	(2; -3)	b	(-2; 3)	c	 (3; 2)	d	(-2; -3)
 9/ Cho elíp (E) : + = 1 và đường tròn (C) : x2 + y2 = 25 có bao nhiêu điểm chung ?
	a	2	b	1	c	4	d	0
 10/ Đường tròn đi qua ba điểm A(0; 3), B(-3; 0), C(3; 0) có pt là :
	a	x2 + y2 -6x -6y + 9 = 0	b	x2 + y2 -9 = 0 
	c	x2 + y2 -6x + 6y = 0	d	x2 + y2 = 3
PhÇn II. Tr¾c nghiÖm tù luËn (6 ®)
C©u 1: Cho ba ®iÓm A(3; 5), B(2; 3), C(6; 2)
	a, ViÕt pt tæng qu¸t cña c¹nh BC vµ ®­êng cao AH cña tam gi¸c ABC
	b, ViÕt pt ®­êng trßn (C) ngo¹i tiÕp tam gi¸c ABC
C©u 2: LËp pt chÝnh t¾c cña elÝp (E) cã mét ®Ønh lµ (0; -2) vµ mét tiªu ®iÓm lµ (-1; 0)
§¸p ¸n vµ thang ®iÓm
PhÇn I. Tr¾c nghiÖm kh¸ch quan: (4 ®)
	(mçi c©u tr¶ lêi ®óng ®­îc 0,4 ®)
C©u 1
C©u 2
C©u 3
C©u 4
C©u 5
C©u 6
C©u 7 
C©u 8
C©u 9
C©u 10
A
D
C
B
B
D
D
C
A
B
PhÇn II. Tr¾c nghiÖm tù luËn: (6 ®)
C©u 1: 
a, = (4; -1) lµ mét vtcp cña BC nªn ta chän = (1; 4) lµ vtpt cña BC (0,5 ®) 
	ViÕt ®­îc pt BC : x + 4y -14 = 0	 (0,5 ®)
	AH lµ ®­êng th¼ng qua A(3; 5) vµ nhËn = (4; -1) lµm vtpt (0,5 ®)
	ViÕt ®­îc pt AH : 4x - y -7 = 0 (0,5 ®)
b, 	Gi¶ sö pt ®­êng trßn cÇn t×m lµ : x2 + y2 + 2Ax + 2By + C = 0
	Thay c¸c täa ®é cña A,B,C vµo pt trªn ta ®­îc hÖ pt
	 (1 ®)
	Gi¶i hÖ t×m ®­îc A = - , B = -, C = 
	Thay vµo ®­îc pt : x2 + y2 -x -y + = 0 (1 ®)
C©u 2: 
	T×m ®­îc b = 2, c = 1 (1 ®)
	a2 = b2 + c2 = 5 (0,5 ®)
	Pt chÝnh t¾c : + = 1 (0,5 ®)
	HÕt