Đề kiểm tra 1 tiết _ lần 1 môn: Giải tích – lớp 12

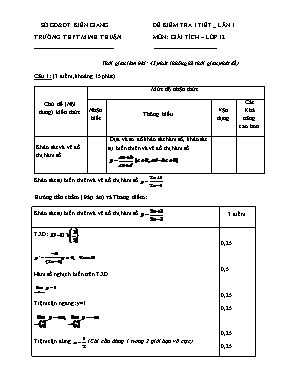
 SỞ GD&ĐT KIÊN GIANG	ĐỀ KIỂM TRA 1 TIẾT _ LẦN 1
TRƯỜNG THPT MINH THUẬN	MÔN: GIẢI TÍCH – LỚP 12
	Thời gian làm bài: 45 phút (không kể thời gian phát đề)
Câu 1: (3 điểm, khoảng 15 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Khảo sát và vẽ đồ thị hàm số.
 Dựa và sơ đồ khảo sát hàm số, khảo sát sự biến thiên và vẽ đồ thị hàm số 
Khảo sát sự biến thiên và vẽ đồ thị hàm số 
Hướng dẫn chấm (Đáp án) và Thang điểm:
Khảo sát sự biến thiên và vẽ đồ thị hàm số 
3 điểm
TXĐ: 	
Hàm số nghịch biến trên TXĐ.	
Tiệm cận ngang: y=1.	
Tiệm cận đứng (Chỉ cần đúng 1 trong 2 giới hạn vô cực)
BBT: 
(Chiều biến thiên y: 0,25; các giá trị đúng: 0,25)	
Đồ thị:
 (2 tiệm cận: 0,25; đồ thị: 0.25) 
0,25
0,5
0,25
0,25
0,25
0,25
0,25
0,5
0,5
Câu 2: (2 điểm, khoảng 8 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Bài toán liên quan đến đồ thị hàm số.
Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đi qua một điểm thuộc đồ thị.
Câu 2 (2 điểm): Cho hàm số . Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x0 = 1.
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 2 (2 điểm): Cho hàm số . Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x0 = 1.
2 điểm
Dạng PTTT: 	
PT: 	
0,5
0,25
0,5
0,5 + 0,25
Câu 3: (2 điểm, khoảng 10 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Bài toán liên quan đến đồ thị hàm số.
Vận dụng khái niệm GTLN, GTNN của hàm số tìm GTLN, GTNN của hàm số trên một đoạn.
Câu 3 (2 điểm): Tìm GTLN, GTNN của hàm số trên [0; 5]
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 3 (2 điểm): Tìm GTLN, GTNN của hàm số trên [0; 5]
2 điểm
Xét: D = [0; 5]	
 (Nghiệm : 0,25; loại (nhận): 0,25)	
Vậy: tại x = 5	
 tại 	
0,25
0,5
0,75
0,25
0,25
Câu 4: (3 điểm, khoảng 12 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Bài toán liên quan đến đồ thị hàm số.
Vận dụng khái niệm cực trị của hàm số, điều kiện để hàm số đạt cực trị tìm m thỏa điều kiện đã cho.
Câu 4 (3 điểm): Cho hàm số . Tìm m để hàm số có một cực đại và một cực tiểu.
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 4 (3 điểm): Cho hàm số . Tìm m để hàm số có một cực đại và một cực tiểu.
3 điểm
Suy ra pt y’=0 luôn có hai nghiệm phân biệt.	
Suy ra hàm số luôn có một cực đại và một cực tiểu với mọi m.
0,75
1,0 
(: 0,5, dấu : 0,5)
0,75
0,5
SỞ GIÁO DỤC VÀ ĐÀO TẠO KIÊN GIANG ĐỀ KIỂM TRA 1 TIẾT _ LẦN 2
 TRƯỜNG THPT MINH THUẬN 	MÔN: GIẢI TÍCH 12
 THỜI GIAN: 45 phút ( Không kể thời gian phát đề)
Câu 1: (6 điểm, khoảng 20 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Phương trình mũ, bất phương trình lôgarit.
Vận dụng kiến thức đã học giải phương trình mũ (đặt ẩn phụ), bất phương trình lôgarit (đưa về cùng cơ số).
Câu 1 (6,0 điểm): Giải các phương trình, bất phương trình sau:
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 1 (6,0 điểm): Giải các phương trình, bất phương trình sau:
6 điểm
Đặt 
Vậy phương trình có nghiệm x = -1.
Đk: 
Kết hợp điều kiện, tập nghiệm của bất phương trình 
0,25 x 2
0,5
0,25 x 2
0,25 x 2
0,25 + 0,5
0,25
0,25 x 2
0,5 + 0,25 
0,5 + 0,5 + 0,25
0,5
Câu 2: (2,5 điểm, khoảng 12 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Lôgarit
Vận dụng qui tắc tính lôgarit tính giá trị biểu thức.
Câu 2 (2,5 điểm): Tính giá trị biểu thức 
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 2 (2,5 điểm): Tính giá trị biểu thức 
2,5 điểm
Vậy A = 2.
0,5 + 0,25
0,5 x 2
0,5 + 0,5
0,25
Câu 3: (1,5 điểm, khoảng 14 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Hàm số mũ.
Vận dụng công thức đạo hàm hàm số mũ tính GTLN, GTNN của hàm số.
Câu 3 ( 1,5 điểm): Tìm GTLN, GTNN của hàm số trên [0; 2].
Hướng dẫn chấm (Đáp án) và Thang điểm:
Tìm GTLN, GTNN của hàm số trên [0; 2].
1,5 điểm.
Hàm số liên tục trên D = [0; 2]
 tại x =2.
 tại x = 0.
0,25
0,5
0,25 
0,25
0,25
 SỞ GD&ĐT KIÊN GIANG	ĐỀ KIỂM TRA 1 TIẾT _ LẦN 3
TRƯỜNG THPT MINH THUẬN	MÔN: HÌNH HỌC – LỚP 12
	Thời gian làm bài: 45 phút (không kể thời gian phát đề)
Câu 1: (3 điểm, khoảng 11 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Thể tích khối lăng trụ.
 Áp dụng công thức đã học tính thể tích khối lăng trụ đứng.
Câu 1 (3 điểm): Cho lăng trụ đứng tam giác ABC.A’B’C’ có tam giác ABC vuông tại B, AB=a, , AA’=4AB. Tính thể tích lăng trụ ABC.A’B’C’ theo a.
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 1 (3 điểm): Cho lăng trụ đứng tam giác ABC.A’B’C’ có tam giác ABC vuông tại B, AB=a, , AA’=4AB. Tính thể tích lăng trụ ABC.A’B’C’ theo a.
3 điểm
ABC.A’B’C’ là lăng trụ đứng nên AA’ là đường cao.
Thể tích lăng trụ: (1)	
(Nếu không chỉ ra AA’ là đường cao nhưng công thức thể tích đúng thì 0,5)
Ta có: (2)	
	 (3)	
Từ (1), (2), (3) suy ra (đvtt)	
0,5
0,25
0,25
0,25
0,25 x 3
0,25 x 2
0,25 x 2
Câu 2a: (4 điểm, khoảng 18 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Thể tích khối chóp.
Áp dụng công thức và các tính chất của hình học không gian tính thể tích khối chóp
Câu 2 : Cho hình chóp S.ABCD có tứ giác ABCD là hình vuông cạnh a. Cạnh bên SA vuông với mp(ABCD), SC hợp với mặt phẳng đáy một góc 600.
(4 điểm) Tính thể tích S.ABCD theo a.
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 2 : Cho hình chóp S.ABCD có tứ giác ABCD là hình vuông cạnh a. Cạnh bên SA vuông với mp(ABCD), SC hợp với mặt phẳng đáy một góc 600.
Tính thể tích S.ABCD theo a.
4 điểm
 a)
Vì nên SA là đường cao.	
Thể tích khối chóp: (1)	
Ta có: (2)	
	AC là hình chiếu vuông góc của SC lên mp(ABCD) nên 	
	 (3)	
Từ (1), (2) và (3) suy ra 	
0,5
0,25
0,25
0,25 x 2
0,5
0,25
0,5
0,25 x 3
0,25 x 2
Câu 2b: (3 điểm, khoảng 16 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Khoảng cách từ một điểm đến mặt phẳng.
 Vận dụng kiến thức đã học tính khoảng cách từ một điểm đến mp.
Câu 2 : Cho hình chóp S.ABCD có tứ giác ABCD là hình vuông cạnh a. Cạnh bên SA vuông với mp(ABCD), SC hợp với mặt phẳng đáy một góc 600.
 (3 điểm) Tính khoảng cách từ A đến mp(SBD).
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 2 : Cho hình chóp S.ABCD có tứ giác ABCD là hình vuông cạnh a. Cạnh bên SA vuông với mp(ABCD), SC hợp với mặt phẳng đáy một góc 600.
 Tính khoảng cách từ A đến mp(SBD).
3 điểm
Gọi O là trung điểm BD.	
Gọi H là hình chiếu vuông góc của A lên SO.	
Chứng minh 	
Suy ra 	
Suy ra: 	
0,25
0,5
0,25
0,5
0,25
0,5
0,75
 SỞ GD&ĐT KIÊN GIANG	 ĐỀ KIỂM TRA CUỐI HỌC KỲ 
TRƯỜNG THPH MINH THUẬN	 	 MÔN : TOÁN_LỚP 12
 Thời gian: 90 phút (Không kể thời gian phát đề)
Câu 1: (3,5 điểm, khoảng 31 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Khảo sát hàm số và một số bài toán liên quan đến đồ thị.
Vận dụng kiến thức đã học vào khảo sát và vẽ đồ thị hàm số đa thức bậc ba.
 Vận dụng kiến thức đã học tìm tham số m thỏa điều kiện đã cho.
Câu 1 (3,5 điểm): Cho hàm số có đồ thị (C)
Khảo sát sự biến thiên và vẽ đồ thị hàm số (C )
Tìm m để đường thẳng cắt đồ thị (C ) tại ba điểm phân biệt.
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 1: Cho hàm số có đồ thị (C)
Khảo sát sự biến thiên và vẽ đồ thị hàm số (C )
Tìm m để đường thẳng cắt đồ thị (C ) tại ba điểm phân biệt.
3,5 điểm
TXĐ: D = R	
HS đồng biến trên , nghịch biến trên 	
HS đạt cực đại tại x = 0, yCĐ = 1; cực tiểu tại x = 1, yCT = 
Bảng biến thiên:
Đồ thị
Đường thẳng cắt đồ thị (C ) tại 3 điểm phân biệt thì phương trình:
 có 3 nghiệm phân biệt	
 có hai nghiệm phân biệt khác 0.	
0,25
0,25
0,25
0,25
0,25
0,25
0,5
0,5
0,25
0,25
0,25
0,25
Câu 2: (2,5 điểm, khoảng 19 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Phương trình mũ, bất phương trình lôgarit.
Vận dụng kiến thức đã học giải phương trình mũ, bất phương trình lôgarit
Câu 2 ( 2,5 điểm): Giải các phương trình và bất phương trình sau:
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 2 Giải các phương trình và bất phương trình sau:
2,5 điểm
 (1)	
Đặt t = 7x, t > 0.	
 (2)
ĐK: x > 1.	
Kết hợp điều kiện, bất phương trình có nghiệm 	
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Câu 3: (1 điểm, khoảng 9 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Hàm số lôgarit.
Tìm tập xác định, tính đạo hàm của hàm số lôgarit.
Câu 3 ( 1 điểm): Tìm tập xác định và tính đạo hàm của hàm số 
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 3 Tìm tập xác định và tính đạo hàm của hàm số 
1,0 điểm
TXĐ: 
Đạo hàm: 
0,25 x 2
0,25
0,25
Câu 4: (3,0 điểm, khoảng 31 phút)
Chủ đề (Nội dung) kiến thức
Mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng
Các Khả năng cao hơn
Khối đa diện.
Khối cầu.
 Tính thể tích khối chóp.
 Xác định tâm, bán kính và tính thể tích khối cầu ngoại tiếp hình chóp.
Câu 4 ( 3 điểm): Cho tứ diện ABCD có AB, AC và AD đôi một vuông góc với nhau. Biết AB=AC=AD=a. 
Tính thể tích tứ diện ABCD.
Xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện ABCD. Tính thể tích khối cầu tương ứng.
Hướng dẫn chấm (Đáp án) và Thang điểm:
Câu 4 Cho tứ diện ABCD có AB, AC và AD đôi một vuông góc với nhau. Biết AB=AC=AD=a. 
Tính thể tích tứ diện ABCD.
Xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện ABCD. Tính thể tích khối cầu tương ứng.
3 điểm
a)
 Thể tích tứ diện ABCD:
b)
Gọi M là trung điểm CD, d là đường thẳng qua M và vuông với mặt phẳng (ACD)	
Mọi điểm trên d cách đều 3 điểm A, C, D. (1)	
Gọi K là trung điểm AB, OK//AM cắt d tại O.	
Khi đó OA = OB (2)	
Từ (1) và (2) suy ra mặt cầu ngoại tiếp tứ diện ABCD tâm O, bán kính R = OA.	
R = OA = .	
Thể tích khối cầu:
 (đvtt)	
0,5
0,25
0,25
0,25 x 2
0,25
0,25
0,25
0,25
0,25
0,25