Đề kiểm tra 1 tiết Chương 2 Hình 7

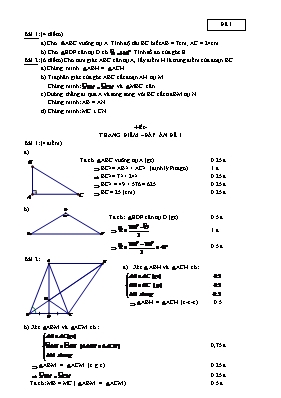
ĐỀ 1
Bài 1: (4 điểm)
a) Cho ABC vuông tại A. Tính độ dài BC biết AB = 7cm; AC = 24cm. 
b) Cho EDF cân tại D có . Tính số đo của góc E.
Bài 2: (6 điểm) Cho tam giác ABC cân tại A, lấy điểm H là trung điểm của đoạn BC. 
 	a) Chứng minh ABH = ACH.
b) Tia phân giác của góc ABC cắt đoạn AH tại M. 
Chứng minh: và MBC cân .
c) Đường thẳng đi qua A và song song với BC cắt tia BM tại N. 
Chứng minh: AB = AN.
d) Chứng minh: MC ^ CN.
-Hết-
THANG ĐIỂM –ĐÁP ÁN ĐỀ 1
Bài 1: (4 điểm)
a) 
 Ta có ABC vuông tại A (gt) 	0.25 đ
 	 BC2 = AB2 + AC2 (định lý Pitago) 	1 đ 
	 BC2 = 72 + 242 	0.25 đ
 BC2 = 49 + 576 = 625 	0.25 đ 
 BC = 25 (cm) 	0.25 đ
b) 
Ta có: EDF cân tại D (gt) 	0.5 đ
 	1 đ
 	 	0.5 đ
Bài 2: 
 Xét ABH và ACH có:
 ABH = ACH (c-c-c) 	 0.5
b) Xét ABM và ACM có :
 	0,75 đ
 ABM = ACM (c.g.c) 	0.25 đ
 	0.25 đ
 Ta có: MB = MC (ABM = ACM)	0.5 đ
 MBC cân tại M 	0.25 đ
c) Ta có:
	 (BM là tia phân giác góc ABC)	0,25 đ
	 (so le trong, AN // BC)	0,25 đ
	=> 	
=> DABN cân tại A	0,25 đ
=> AB = AN	0,25 đ 
d) 	Chứng minh đúng ACN cân tại A => 	0.25 đ
Chứng minh đúng 	0,25 đ
Ta có: 
	(2 góc trong cùng phía, AN // BC)
	 (chứng minh trên)
=> => 	0.25 đ
=>
=> MC ^ CN	0,25 đ
- HẾT -
ĐỀ 2
Bài 1: (4 điểm)
a) Cho ABC vuông tại A. Tính độ dài BC biết AB = 8cm; AC = 15cm. 
b) Cho EDF cân tại E có . Tính số đo của góc E.
Bài 2: (6 điểm) 
Cho tam giác ABC cân tại A (AB > BC), lấy điểm M là trung điểm của đoạn BC. 
 	a) Chứng minh ABM = ACM.
b) Tia phân giác của góc ACB cắt đoạn AM tại I. 
Chứng minh: và IBC cân .
c) Đường thẳng đi qua B và song song với AC cắt tia CI tại H. Chứng minh: BH = BC.
d) Đường thẳng đi qua H và song song với BC cắt đoạn AB tại K. 
Chứng minh: BK = BC.
-Hết-
THANG ĐIỂM –ĐÁP ÁN ĐỀ 2
Bài 1: (4 điểm)
a) 
 	 Ta có ABC vuông tại A (gt) 	0.25 đ
 	 BC2 = AB2 + AC2 (định lý Pitago) 	1 đ 
	 BC2 = 82 + 152 	0.25 đ
 BC2 = 64 + 225 = 289 	0.25 đ 
 BC = 17 (cm) 	0.25 đ
b) +
Ta có: EDF cân tại E (gt) 	0.5 đ
 	1 đ
 	 	0.5 đ
Bài 2: 
 Xét ABM và ACM có:
 ABM = ACM (c-c-c) 	 0.5
b) Xét ABI và ACI có :
 	0,75 đ
 ABI = ACI (c.g.c) 	0.25 đ
 	0.25 đ
 Ta có: IB = IC (ABI = ACI)	0.5 đ
 IBC cân tại I 	0.25 đ
c) Ta có:
	 (BM là tia phân giác góc ABC)	0,25 đ
	 (so le trong, AN // BC)	0,25 đ
	=> 	
=> DBCH cân tại A	0,25 đ
=> BH = BC	0,25 đ 
d) 	Ta có: 
	(2 góc so le trong, BH // AC)
	 (2 góc so le trong, HK // BC)
=> 
=> 	0.25 đ
Mả 	 (DABC cân tại A)
	(so le trong, HK // BC)	
Nên 	0.25 đ
=> DBHK cân tại B
=> BH = BK	0.25 đ
Mà BH = BC (chứng minh trên)
Nên BK = BC	0,25 đ
- HẾT -