Đề khảo sát kỳ thi THPT quốc gia Toán - Năm học 2016-2017 - Trường THPT Nguyễn Trường Thúy

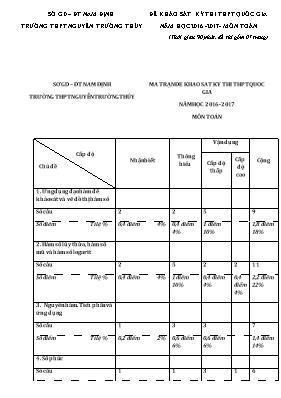
SỞ GD – ĐT NAM ĐỊNH
TRƯỜNG THPT NGUYỄN TRƯỜNG THÚY
ĐỀ KHẢO SÁT KỲ THI THPT QUỐC GIA
NĂM HỌC 2016 -2017- MÔN TOÁN
 (Thời gian 90 phút, đề thi gồm 07 trang)
SỞ GD – ĐT NAM ĐỊNH
TRƯỜNG THPT NGUYỄN TRƯỜNG THÚY
MA TRẬN ĐỀ KHẢO SÁT KỲ THI THPT QUỐC GIA
NĂM HỌC 2016 -2017
MÔN TOÁN
 Cấp độ
 Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Số câu 
2
2
5
9
Số điểm Tỉ lệ %
0,4 điểm 4% 
0,4 điểm 4% 
1 điểm 10% 
1,8 điểm 18% 
2. Hàm số lũy thừa, hàm số mũ và hàm số logarit 
Số câu 
2
5
2
2
11
Số điểm Tỉ lệ %
0,4 điểm 4% 
1 điểm 10% 
0,4 điểm 4% 
0,4 điểm 4% 
2,2 điểm 22% 
3. Nguyên hàm. Tích phân và ứng dụng
Số câu 
1
3
3
7
Số điểm Tỉ lệ %
0,2 điểm 2% 
0,6 điểm 6% 
0,6 điểm 6% 
1,4 điểm 14% 
4. Số phức
Số câu 
1
1
3
1
6
Số điểm Tỉ lệ %
0,2 điểm 2% 
0,2 điểm 2% 
0,6 điểm 6% 
0,2 điểm 2% 
1,2 điểm 12% 
5. Khối đa diện
Số câu 
2
3
1
6
Số điểm Tỉ lệ %
0,4 điểm 4% 
0,6 điểm 6% 
0,2 điểm 2% 
1,2 điểm 12% 
6. Mặt nón, mặt trụ, mặt cầu
Số câu 
1
1
1
3
Số điểm Tỉ lệ %
0,2 điểm 2% 
0,2 điểm 2% 
0,2 điểm 2% 
0,6 điểm 6% 
7. Phương pháp tọa độ trong không gian
Số câu 
3
2
2
1
8
Số điểm Tỉ lệ %
0,6 điểm 6% 
0,4 điểm 4% 
0,4 điểm 4% 
0,2 điểm 2% 
1,6 điểm 16% 
Tổng số câu 
12
17
17
4
50
Số điểm Tỉ lệ %
2,4 điểm 24% 
3,4 điểm 34% 
3,4 điểm 34% 
0,8 điểm 8% 
10 điểm 100% 
(TH) Cho hàm số y = x4 - 2x3 - 3. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (0;+∞).	B. Hàm số nghịch biến trên khoảng (-∞;0).
C. Hàm số đồng biến trên khoảng (1;+∞).	D. Hàm số nghịch biến trên khoảng (-1;0).
(VDT) Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số fx=x+9x trên đoạn [1;4]. Tính hiệu M -m?
A. M-m=14	B. M-m=154	C. M-m=16	D. M-m=4
 (VDT) Gọi A(x0; y0) là một giao điểm của đồ thị hàm số y = x3 - 3x + 2 và đường thẳng y = x +2. Tính hiệu y0 - x0.
A. y0 - x0 = 4	B. y0 - x0 = -2 	C. y0 - x0 = 6 	D. y0 - x0 = 2
(TH) Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? 
A. y = -x3- 3x2 +4	B. y = x3- 3x2 -4	
C. y = x3+ 3x2 -4	D. y = - x33+x2 - 4
(NB) Cho hàm số y = f(x) xác định và có đạo hàm f '(x). Biết rằng hình vẽ bên là đồ thị của hàm số f '(x). Khẳng định nào sau đây là đúng về cực trị của hàm số f(x)?
A. Hàm số f(x) đạt cực đại tại x = -1 	
B. Hàm số f(x) đạt cực tiểu tại x = 1
C. Hàm số f(x) đạt cực tiểu tại x = -2	
D. Hàm số f(x) đạt cực đại tại x = -2
(VDC) Tìm tất cả các giá trị thực của m sao cho đồ thị hàm số y=2x-(m-1)x2+1x-1 có đúng hai tiệm cận ngang ?
A. m=1	B. (1;4)È (4;+∞)	C. m 1
(TH) Tìm m để hàm số y = x3 - 3mx2 + (m2 - 1)x đạt cực đại tại x = 0?
A. m = 0	B. m = 1 hoặc m = -1	C. m= -1.	D. m = 1
(VDC) Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của m để phương trình m=f(x)có hai nghiệm phân biệt ?
A. m=0 hoặc m > 2	
B. m =2 hoặc m > -1	
C. m > - 1	
D. m > 2
 (NB) Cho hàm số y=2x+1x-1. Số tiệm cận của đồ thị hàm số là:
A. 3	B. 2	C. 1	D. 0
(TH) Hàm số y = 2017x có đạo hàm là:
A. y' = 2017x	B. y' = 2017x.ln2017	C. y'=2017xln2017	D. y' = x.2017x-1
 (NB) Trong các đồ thị dưới đây, đồ thị nào là dạng của đồ thị hàm số y = ax với a >1?
A. Hình 3 	B. Hình 1 	C. Hình 4 	D. Hình 2
(NB) Tìm tập xác định của hàm số 
A. 	B. 	
C. 	D. 
(TH) Tập xác định của hàm số y=log2-x2+4x-3 là:
A. (-∞;1)È (3;+∞)	B. (-∞;1]È[3;+∞)	C. (1;3)	D. [1;3]
 (TH) Tìm m để phương trình có đúng 2 nghiệm 
A. B. 	C. D. 
(VDT) Giải phương trình . Ta có nghiệm:
A. và 	B. và 
C. và 	D. và 
(NB) Trong các phương trình sau đây, phương trình nào có nghiệm?
A. 	B.	C.	D.
(NB) Bất phương trình tương đương với bất phương trình nào dưới đây?
A. 	B. 
C. 	D. 
 (VDT) Tích phân . Khi đó m.n bằng: 
A. B. C. 	D. 
(TH) Cho hình phẳng (H) giới hạn bởi và Ox. Thể tích khối tròn xoay sinh ra khi quay (H) quanh Ox bằng:
A. 	B. 	C. 	D. 
 (VDT) Tích phân bằng:
A. 	B. 	C. 	D. 
(TH) Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số và các trục tọa độ. Chọn kết quả đúng nhất
A. 	B. 	C. 	D. 
(VDT) Họ nguyên hàm của hàm số là:
A.	B.
C. 	D. 
(VDT) Họ nguyên hàm của hàm số là:
A. 	B. 
C. 	D. 
 (VDT) Hàm số nào sau đây không là nguyên hàm của hàm số ?
A. 	B. 	C. 	D. 
(TH) Nếu với thì bằng:
A. 	B.7 	C.0 	D.3
(TH) Cho biết , vậy ?
A.	B. 
C. 	D. 
(VDT)Họ nguyên hàm của hàm số . Khi đó bằng:
A.10	B.	C. 	D. Số khác
(TH) Diện tích hình phẳng giới hạn bởi đồ thị của hàm số và các trục tọa độ là biểu thức có dạng . Khi đó m.n bằng:
A. 	B. 	C. Số khác	D.
(TH) Cho hai số phức z1 = 4 + i và z2 = 1 - 3i. Tính môđun của số phức z1 - z2.
A.z1-z2=17-10	B.z1-z2=13
C.z1-z2=25	D.z1-z2=5
 (TH) Cho số phức z = 5 + 2i.Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng -5 và phần ảo bằng -2.	B. Phần thực bằng 5 và phần ảo bằng 2.
C. Phần thực bằng 5 và phần ảo bằng -2.	D. Phần thực bằng 5 và phần ảo bằng -2i.
(TH) Kí hiệu z1, z2, z3, z4 là bốn nghiệm phức của phương trình z4 - 3z2 - 4 = 0. Tính T=z1+z2+z3+z4
A. T = 3	B. T = 0.	C. T = 4 + 2. 	D.T = 4
(VDT) Cho số phức z thỏa mãn (2 - i)z = (2 + i)(1- 3i). Gọi M là điểm biểu diễn của z. Khi đó tọa độ điểm M là:
A. M(3;1)	B. M(3;-1) 	C. M(1;3) 	D. M(1;-3)
 (TH) Cho số phức z có phần ảo âm, gọi w = 2z + z-zi. Khi đó khẳng định nào sau đây về W là đúng ?
A.w là số thực.	B.w có phần thực bằng 0 
C. w có phần ảo bằng 0	D. w có phần ảo dương
(VDT) Gọi T là tập hợp các số phức z thỏa mãn z-i≥3 và z-1≤5.Gọi z1, z2 Î T lần lượt là các số phức có mô đun nhỏ nhất và lớn nhất. Tìm số phức
A.2-2i 	B.-2+12i 	C.6-4i 	D.12+4i
(TH) Cho một hình hộp chữ nhật có 3 mặt có diện tích bằng 12, 15 và 20. Tính thể tích của hình hộp chữ nhật đó.
A.	B.	C.	D.
(TH) Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân, , SA vuông góc với mặt phẳng đáy và . Tính thể tích V của khối chóp S.ABC
A.	B.	C.	D.
(TH) Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy và SB tạo với mặt đáy một góc . Tính thể tích V của khối chóp S.ABC
A.	B.	C.	D.
(VDC) Cho một tấm bìa hình vuông cạnh 5 dm.Để làm một mô hình kim tự tháp Ai Cập, người ta cắt bỏ 4 tam giác cân bằng nhau có cạnh đáy chính là cạnh của hình vuông rồi gập lên, ghép lại thành một hình chóp tứ giác đều. Để mô hình có thể tích lớn nhất thì cạnh đáy của mô hình là:
A.	B.	
C.	D.
(TH) Cho khối chóp S.ABCDcó đáy là hình vuông tâm O, .Hình chiếu vuông góc của S trên mặt phẳng ABCD trùng với trung điểm OA. Góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD) bằng . Tính thể tích V của khối chóp S.ABCD.
A.	B.	C.	D. 
(TH) Gọi S là diện tích xung quanh của hình nón tròn xoay được sinh ra bởi đoạn thẳng AC’ của hình lập phương ABCD.A’B’C’D’ có cạnh khi quay xung quanh trục AA’. Diện tích S là: 
A.	B.	C.	D.
(TH) Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng , một hình nón có đỉnh là tâm của hình vuông ABCD và có đường tròn đáy ngoại tiếp hình vuông A’B’C’D’. Diện tích xung quanh của hình nón đó là :
A.	B.	C.	D.
(VDT) Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy bằng hình tròn lớn của quả bóng bàn và chiều cao bằng ba lần đường kính của quả bóng bàn. Gọi là tổng diện tích của ba quả bóng bàn, là diện tích xung quanh của hình trụ. Tỉ số bằng:
A.1 	B. 2 	C.	D.
 (TH) Mặt phẳng chứa hai điểm và và song song với trục Ox có phương trình là:
A.x+2z-3=0	B. y-2z+2=0 	C.2y-z+1=0 	D. x+y-z=0
(TH) Tìm giao điểm của d : và mặt phẳng 
A.	B.	C.	D.
(TH) Cho đường thẳng đi qua điểm và có vec tơ chỉ phương . Phương trình tham số của đường thẳng là:
A.	B.	C.	D.
 (TH) Mặt cầu (S) có tâm và tiếp xúc với mặt phẳng 
A.	B.
C.	D.
(VDT) Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: và mặt phẳng . Tìm tọa độ điểm có tọa độ âm thuộc d sao cho khoảng cách từ đến bằng 2.
A.	B.	C.	D.
(VDT) Trong không gian với hệ tọa độ Oxyz, cho . Gọi M là điểm nằm trên cạnh BC sao cho MC = 2MB. Độ dài đoạn AM là:
A.	B.	C.	D.
(VDT) Trong không gian với hệ tọa độ Oxyz, chovà đường thẳng d: . Tìm điểm M thuộc d để thể tích tứ diện MABC bằng 3.
A.	B.
C.	D.
(VDT) Trong không gian với hệ tọa độ Oxyz, cho Viết phương trình mặt phẳng (P) đi qua A, B và (P) tạo với mặt phẳng (Oyz) góc thỏa mãn 
A.	B.
C.	D.