Đáp án đề nghị kì thi olympic ĐBSCL Sóc Trăng năm học 2008 – 2009 môn Toán

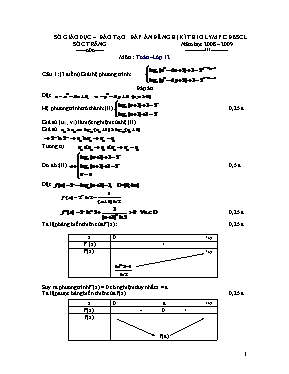
	SỞ GIÁO DỤC – ĐÀO TẠO	ĐÁP ÁN ĐỀ NGHỊ KÌ THI OLYMPIC ĐBSCL
	 SÓC TRĂNG	Năm học 2008 – 2009
	-----o0o-----	----------///----------
Môn : Toán –Lớp 12
Câu 1: (3 điểm) Giải hệ phương trình: 	
Đáp án
Đặt 
Hệ phương trình trở thành: (II) 	0,25 đ
Giả sử (u0 ; v0) là một nghiệm của hệ (II). 
Giả sử 	
Tương tự 	
Do đó: (II) 	0,5 đ
Đặt 
	0,25 đ
Ta lập bảng biến thiên của f’(x):	0,25 đ
x
0 +¥
f”(x)
+
f'(x)
 +¥
Suy ra phương trình f’(x) = 0 có nghiệm duy nhất x = a.
Ta lập được bảng biến thiên của f(x)	0,25 đ
x
0 a +¥
f'(x)
 - 0 +
f(x)
 f(a)
Suy ra phương trình (1) có nhiều nhất hai nghiệm	0,25 đ
Mặt khác, ta nhận thấy x=0, x=1 là nghiệm của phương trình (1).
Vậy phương trình (1) có đúng hai nghiệm là x=0, x=1.	0.5 đ
Suy ra hệ (II) có hai nghiệm là (0;0) và (1;1)	0,25 đ
Suy ra hệ phương trình đã cho có 5 nghiệm: (2; 2), (1; 1), (3; 3), (1; 3), (3; 1)	0,5 đ
Câu 2: Cho đường tròn (O) ngoại tiếp tam giác ABC. Đường phân giác trong của góc A cắt đường tròn tại D (D khác A). Chứng minh AB + AC < 2AD.
Đáp án
Cách 1:
Kẻ dây cung DE//AB
Ta có 	0,25 đ
Þ BD = AE	0,25 đ
Þ BE = AD	0,5 đ
Ta cũng có
Þ CD = AE	0,25 đ
Þ AC = DE	0,25 đ
Gọi I, J lần lượt là trung điểm của AB và DE; K là giao điểm của AD và BE.
ABDE là hình thang cân hoặc hình chữ nhật nên ta có:
I, J, K thẳng hàng	0,25 đ
IJ vuông góc với AB và DE	0,25 đ
Ta có 
AD = AK + KD > AI + DJ = ½(AB+AC)	0,75 đ
Þ 2AD > AB + AC	0,25 đ
Cách 2:
Gọi R là bán kính đường tròn ngoại tiếp:
Tá có:	
AB = 2RsinC, AC = 2RsinB
Suy ra 2AD > AB + AC
Câu 3: (2 điểm) Tìm các nghiệm nguyên của phương trình 
Đáp án
Giả sử bộ ba số nguyên (x0; y0; z0) là nghiệm của phương trình.
Dễ thấy nếu một trong ba số trên bằng 0 thì hai số còn lại cũng bằng 0 Þ (0; 0; 0) là một nghiệm của phương trình.	0,25 đ
Nếu cả ba số đều khác 0, đặt d = (x0, y0, z0) ta có
x0 = dx1 , y0 = dy1 , z0 = dz1 với x1, y1, z1 nguyên.	0,25 đ
Ta được Þ x1 chia hết cho 3. Đặt x1 =3x2, ta được	0,25 đ
 Þ y1 chia hết cho 3. Đặt y1 =3y2, ta được	0,25 đ
 Þ y1 chia hết cho 3.	0,25 đ
Þ x1, y1, z1 có ước chung là 3 (mâu thuẫn)	0,5 đ
 Vậy phương trình chỉ có một nghiệm nguyên duy nhất là (0; 0;0)	0,25 đ
Câu 4: (3 điểm) Cho dãy số (un) xác định bởi
Chứng minh rằng dãy số (un) có giới hạn hữu hạn và tìm giới hạn của dãy số.
Đáp án
Đặt 
Hàm số f(x) tăng trên [0;1] và 
. Bằng qui nạp, chứng minh được 	0,5 đ
Mặt khác 
Bằng qui nạp, chứng minh được dãy (un) giảm.	0,75 đ
Dãy số giảm và bị chặn dưới bởi 0 nên có giới hạn hữu hạn.	0,25 đ
Gọi l là giới hạn của dãy số, do dãy số bị chặn dưới bởi 0, bị chặn trên bởi ½ nên 
 (*)	0,5 đ
Chuyển qua giới hạn khi n tiến tới +¥ trong biểu thức truy hồi ta được:
	0,5 đ
Kết hợp với (*) suy ra l = 0.	0,5 đ
Câu 5: (3 điểm) Phương trình x + y + z + t = 2009 có bao nhiêu nghiệm nguyên dương?
(Nghiệm (x, y, z, t) với x, y ,z, t là các số nguyên dương)
Đáp án
x + y + z + t = 2009 (1)
Đặt a = x – 1, b = y – 1, c = z – 1, d = t – 1.
Ta thấy a, b, c, d là các số tự nhiên thỏa phương trình:
a + b + c + d = 2005 (2)
và tương ứng giữa các bộ số (a, b, c, d) và (x, y, z, t) là tương ứng một – một (song ánh).
Ta tìm số nghiệm tự nhiên của phương trình (2)
Ta thấy mỗi nghiệm tự nhiên của phương trình (2) là một bộ 4 số tự nhiên (a, b, c, d) thỏa điều kiện a + b + c + d = 2005.
Với mỗi bộ 4 số (a, b, c, d) như vậy ta đặt tương ứng với một dãy nhị phân (dãy gồm các chữ số 0 và 1) theo qui tắc sau: viết từ trái sang phải: 
a số 1 liên tiếp – số 0 – b số 1 liên tiếp – số 0 – c số 1 liên tiếp – số 0 – d số 1 liên tiếp.
Như vậy mỗi bộ (a, b, c, d) tương ứng một – một với một dãy nhị phân gồm 2008 kí tự, trong đó có đúng 2005 kí tự “1” và 3 kí tự “0”.
Mặt khác, một dãy nhị phân độ dài 2008, trong đó có đúng 3 kí tự “0” tương ứng với một cách chọn 3 phần tử từ 2008 phần tử.
Số các dãy nhị phân như trên là 
Từ đó suy ra số nghiệm của phương trình (1) là 
Câu 6: (3 điểm) Tìm tất cả các đa thức P(x) có bậc nhỏ hơn 2009 và thỏa mãn điều kiện:
Đáp án
Cách 1:
Đặt 	0,5 đ
Ta có: 	0,5 đ
Đặt 
Ta có: 	0,5 đ
 (d là hằng số bất kì)	0,5 đ
	0,5 đ
Vậy các đa thức cần tìm có dạng với d là số thực bất kì	0,5 đ
Cách 2:
Từ (1)
Þ 	0,25 đ
Þ (k là hằng số)	0,25 đ
Þ P(x) có bậc nhỏ hơn hoặc bằng 3.	0,25 đ
Đặt 	0,25 đ
Từ (1) ta có 	0,5 đ
	0,5 đ
Thử lại ta thấy các đa thức 
 với d là số thực bất kì đều thỏa mãn (1)	0,5 đ
Vậy các đa thức cần tìm có dạng với d là số thực bất kì	0,5 đ
Câu 7: (3 điểm) Trong mặt phẳng với hệ tọa độ Oxy cho hai đường tròn:
Một đường thẳng (d) đi qua giao điểm của (C1) và (C2) lần lượt cắt lại (C1) và (C2) tại M và N. Tìm giá trị lớn nhất của đoạn MN.
Đáp án
(C1) có tâm I(2; 3) và bán kính R =
(C2) có tâm J(-2; 0) và bán kính r = 2	0,25 đ
Þ IJ = 5	0,25 đ
Þ |R – r| < IJ < R + r
Þ (C1) và (C2) cắt nhau tại hai điểm A và B.	0,25 đ
Giả sử (d) qua B, gọi (d’) là đường thẳng qua A, cắt (C1), (C2) lần lượt tại C và D.
CD vuông góc với AB nên B, I, C thẳng hàng; B, J, D thẳng hàng	0,25 đ
Þ CD = 2IJ = 10	0,25 đ
Ta có:
MC^MN, ND^MN Þ MC//ND	0,5 đ
Þ MN = d(MC, ND)	0,25 đ
Þ MN £ CD	0,5 đ
Þ max MN = CD = 10 đạt được khi d//IJ	0,5 đ
_______________________