Công thức lượng giác đáng nhớ

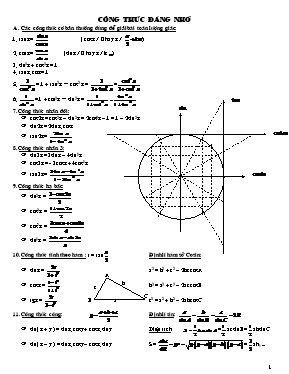
	COÂNG THÖÙC ÑAÙNG NHÔÙ	
A . Caùc coâng thöùc cô baûn thöôøng duøng ñeå giaûi baøi toaùn löôïng giaùc:
1. tanx = 	( cosx ≠ 0 hay x ≠ )
2. cotx = 	(sinx ≠ 0 hay x ≠ k)
3. sin2x + cos2x = 1
4. tanx.cotx = 1
5. = 1 + tan2x " cos2 x = =
6. = 1 + cot2x " sin2x = 
7. Coâng thöùc nhaân ñoâi: 
cos2x = cos2x – sin2x = 2cos2x – 1 = 1 – 2sin2x
sin2x = 2sinx.cosx
tan2x = 
8. Coâng thöùc nhaân 3:
sin3x = 3sinx – 4sin3x
cos3x = - 3cosx + 4cos3x
tan3x = 
9. Coâng thöùc haï baäc:
sin2x = 
cos2x = 
cos3x = 
sin3x = 
10. Coâng thöùc tính theo haøm : t = tan	Ñònh lí haøm soá Cosin:
A
sinx = 	a2 = b2 + c2 – 2bccosA
c
b
C
cosx = 	b2 = a2 + c2 – 2accosB
a
B
tgx = 	c2 = a2 + b2 – 2abcosC
11. Coâng thöùc coäng:	 	Ñònh lí sin: 
sin( x + y ) = sinx.cosy + cosx.siny	Dieän tích: 	=acsinB =absinC
sin( x – y ) = sinx.cosy – cosx.siny	S = =aha 
cos(x + y ) = cosx.cosy – sinx.siny	 	- cosx = sin( x - )
cos(x – y ) = cosx.cosy + sinx.siny	- cosx = cos(p - x)
tan( x + y ) = 	- sinx = sin(-x)
tan(x – y ) = 	- sinx = cos(x + )
12. Coâng thöùc bieán ñoåi tích thaønh toång:	sinx = cos( - x)
cosx.cosy = [cos( x – y ) + cos(x + y)]	cosx = sin( - x)
sinx.siny = [cos( x – y ) – cos(x + y)]	sinx = ± 1 Û x = ± + k2p
sinx.cosy = [sin( x – y ) + sin(x + y)]	sinx = 0 Û x = kp	
13. Coâng thöùc bieán ñoåi toång thaønh tích:	cox = 0 Û x = + kp
cosx + cosy = 2cos	cosx = 1 Û x = k2p
cosx – cosy = - 2	cosx = -1 Û x = p + k2p
sinx + siny = 2	tanx = 0 Û x = kp
sinx – siny = 2	tanx = ± 1 Û x = ± + kp
14. Caùc phöông trình löôïng giaùc cô baûn:	cotx = 0 Û x = + kp 
	 x = y + k2p 	cotx = ± 1 Û x = ± + kp
sinx = sin y 	 	1 + sin2x = 
 x = p - y + k2p	1 – sin2x = 
cosx = cosy x = ± y + k2	1 + cos2x = 2
tanx = tany x = y + k (nhôù ñieàu kieän cosx ¹ 0)	1 – cos2x = 2
cotx = coty Û x = y + kp (nhôù ñieàu kieän sinx ¹ 0)
Daïng cuûa phöông trình
Caùch giaûi
Phöông trình baäc nhaát hoaëc baäc hai ñoái vôùi f(x), trong ñoù f(x) laø moät bieåu thöùc löôïng giaùc naøo ñoù
Ñaët aån phuï t = f(x)
Phöông trình baäc nhaát ñoái vôùi sinx vaø cosx:
 Asinx + Bcosx = C ( ñk: A2+ B2 ³ C2 )
Ñaët z = , chia 2 veá cho z, ñöa veà daïng sin ( x ± ) = sinu hoaëc cos(x 
Phöông trình thuaàn nhaát baäc hai ñoái vôùi sinx vaø cosx coù daïng nhö sau:
 Asin2x + Bsinx.cosx + Ccos2x = 0 
Coù 2 caùch giaûi:
Caùch 1: Haï baäc roài ñöa veà daïng Asinx + Bcosx = C
Caùch 2:
B1: Thöû xem cosx = 0 coù phaûi laø nghieäm cuûa phöông trình khoâng
B2: Chia hai veá cho cos2x, roài giaûi bình thöôøng
Phöông trình ñoái xöùng ñoái vôùi sinx vaø cosx coù daïng:
 A(sinx ± cosx) + Bsinx.cosx + C = 0
Ñaët t = sinx ± cosx ñeå giûaûi, ñk t 
Neáu t = sinx + cosx Þ sinxcosx = 
Neáu t = sinx – cosx Þ sinxcosx = 
Phöông trình khaùc, khoâng thuoäc caùc daïng treân
Baèng phöông phaùp bieán ñoåi ñeå ñöa veà daïng cô baûn
Löu yù: 	1/ sinx + cosx = sin( x + ) = cos(x - )
2/ sinx – cosx = sin( x - ) = - 
3/ sin4x + cos4x = 1 - sin22x = 	(coâng thöùc giaûi nhanh)
 + = + = + = =1 - sin22x = 
4/ sin6x + cos6x = 1 - sin22x = (coâng thöùc giaûi nhanh)
 + = + = + = = 1-sin22x = 
B. Baøi taäp:
Baøi 1: Phöông trình baäc nhaát hoaëc baäc hai ñoái vôùi f(x)
a/ sin(3x - 	b/ sin(3x – ) = -1
c/ = 1	d/ cos(3x – 150 ) = -cos1350
e/ tan(2x + ) = tan	f/ cot( 450 – x) = tan
g/ sin3x – cos2x = 0	h/ sin(x + 
i/ sin(3x - 	j/ cos
k/ cos2x = - sin (x + )	l/ sin
m/ 3sin22x + 7cos2x – 3 = 0	n/ 6cos2x + 5sinx – 7 = 0
0/ cos2x – 5sinx – 3 = 0	p/ cos2x + cosx +1 = 0
q/ 6sin23x + cos12x = 1	r/ 4sin4x + 12cos2x = 7
s/ 3cot2(x + 	t/ tan2(2x - 
u/ 7tanx – 4cotx = 12	v/ cot2x + ( - 1)cotx - = 0 	y/ 3sin2x + 2cos2x = 3
w/ 4sinx – 3cosx = 5	x/ 3cosx + 2sinx = 	 z/ 2sin2x + 3cos2x = sin14x
Baøi 2: Phöông trình thuaàn nhaát baäc hai ñoái vôùi sinx vaø cosx coù daïng nhö sau:
Asin2x + Bsinx.cosx + Ccos2x = 0 (ñk: A2 + B2 + C2 ≠ 0)
a/ 2sin2x + ( 1 - )sinx.cosx + ( 1 - )cos2x = 1
b/ 4sin2x + 3sin2x – 2cos2x = 4
c/ sin3x + cos3x + 2cosx = 0
d/ = 0
e/ = 3(cos2x + sinx.cosx)
f/ = 3sinx
* (2sinx – 1)(2cos2x + 2sinx + m) = 3 - 4. Tìm m ñeå phöông trình coù 2 nghieäm thoaû ñieàu kieän 0 £ x£p
Baøi 3: Phöông trình ñoái xöùng ñoái vôùi sinx vaø cosx coù daïng: A(sinx ± cosx) + Bsinx.cosx + C = 0
a/ 3(sinx + cosx) + 2sin2x + 3 = 0
b/ sinx – cosx + 4sinx.cosx + 1 = 0
c/ sin2x – 12(sinx – cosx) + 12 = 0
d/ sin3x + cos3x = 0
e/ sinx.cosx - (sinx + cosx) + 1 = 0
f/ sin3x + cos3x = 
Baøi 4: Phöông trình ñöa veà daïng tích:
a/ sin5x + sinx – sin3x = 0
b/ cos2x – cos6x = sin3x + sin5x 
c/ (sinx – cosx)2 – ( + 1 )(sinx – cosx) + = 0
d/ tan + sinx = 2
e/ sinx + sin2x + sin3x = (cosx + cos2x + cos3x)
f/ sinx + sin2x + sin3x = 4cos
g/ tanx + tan2x= tan3x
Baøi 5: Duøng coâng thöùc haï baäc
a/ sin4x + cos4x = 
b/ sin6x + cos6x = sin4x + cos4x
c/ sin4x – sin2x – 2 = 0
d/ sin4x + cos4x – cos2x = 1 - 
e/ tan2x + cot2x – 2 = 0
Baøi 6: Caùc daïng phöông trình khaùc
a/ sin2x – 2sinxcosx – 3cos2x = 0	
b/ 6sin2x + sinx.cosx – cos2x = 2
c/ sin2x – 2sin2x = 2cos2x	
d/ 2sin22x – 3sin2x.cos2x + cos22x = 2
e/ 4sinx.cos(x – ) + 4sin( + x).cosx + 2sin().cos( + x) = 1
f/ 2sin3x + 4cos3x = 3sinx	
g/ 3 + 3
h/ sinx.sin7x = sin3x.sin5x	
i/ sin5x.cos3x = sin9x.cos7x
j/ cosx.cos3x – sin2x.sin6x – sin4x.sin6x = 0	
k/ sin4x.sin5x + sin4x.sin3x – sin2x.sinx = 0
l/ sin5x + sin3x = sin4x
m/ sinx + sin2x + sin3x = 0
n/ cosx + cos3x + 2cos5x = 0
o/ cos22x + 3cos18x + 3cos14x + cos10x = 0
p/ sin2x + sin22x + sin23x = 
q/ sin23x + sin24x = sin25x + sin26x
r/ sin22x + sin24x = sin26x
s/ cos2x + cos22x + cos23x + cos24x = 2
t/ cos23x + cos24x + cos25x = 
u/ 8cos4x = 1 + cos4x
v/ sin4x + cos4x = cos4x
w/ 3cos22x – 3sin2x + cos2x = 0
x/ tan(x + + cot(
y/ tan
z/ tan
z1/ sin2x + 2cotx = 3
z2/ tanx = 1 – cos2x
z3/ tan( x – 150).cot(x + 150) = 
z4/ sin2x + 2cos2x = 1 + sinx – 4cosx
z5/ 3sin4x + 5cos4x – 3 = 0
z6/ (2sinx – cosx).(1 + cosx) = sin2x
z7/ 1 + sinx.cos2x = sinx + cos2x
z8/ sin2x.tanx + cos2x.cotx – sin2x = 1 + tanx + cotx
z9/ tancosx – sinx.cos3x = 
z10/ sin2x + sinx.cos4x + cos24x = 
z11/ (2sinx – 1).(2sin2x + 1) = 3 – 4cos2x
z12/ cos
z13/ 6tan
z14/ 3cos2x + 2(1 + 
z15/ 2(sinx + cosx).cosx = 3 + cos2x
z16/ cos2x - sin2x = 1 + sin2x
z17/ 4sinx.cosx + 4cos2x – 2sin2x = 
z18/ sin()cot3x + sin( + 2x) - cos5x = 0
z19/ tan2x + cos4x = 0
z20/ 9sinx + 6cosx – 3sin2x + cos2x = 8
z21/ sin4(x + ) = + cos2x – cos4x
z22/ (2sinx + 1).(3cos4x + 2sinx – 4) + 4cos2x = 3
z23/ sin3(x + ) = 2sinx
z24/ 2sinx + cotx = 2sin2x + 1
z25/ tan2x(1 – sin3x) + cos3x – 1 = 0
z26/ 1 + cot2x = 
z27/ 6sinx – 2cos2x =