Chuyên đề Số phức – Đề 005

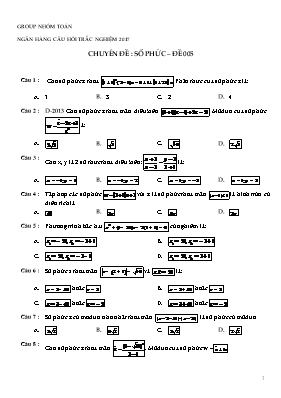
GROUP NHÓM TOÁN
NGÂN HÀNG CÂU HỎI TRẮC NGHIỆM 2017
CHUYÊN ĐỀ : SỐ PHỨC – ĐỀ 005
C©u 1 : 
 Cho số phức z thỏa .Phần thực của số phức z là: 
A.
1
B.
3
C.
2
D.
4
C©u 2 : 
D-2013 Cho số phức z thỏa mãn điều kiện . Môdun của số phức là: 	
A.
B.
C.
D.
C©u 3 : 
Cho x, y là 2 số thực thỏa điều kiện: là:
A.
B.
C.
D.
C©u 4 : 
Tập hợp các số phức với z là số phức thỏa mãn là hình tròn có diện tích là
A.
B.
C.
D.
C©u 5 : 
Phương trình bậc hai có nghiệm là:
A.
B.
C.
D.
C©u 6 : 
Số phức z thỏa mãn và là:
A.
 hoặc 
B.
 hoặc 
C.
 hoặc 
D.
 hoặc 
C©u 7 : 
Số phức z có modun nhỏ nhất thỏa mãn là số phức có môđun
A.
B.
C.
D.
C©u 8 : 
Cho số phức z thỏa mãn . Môđun của số phức w =
A.
B.
8	
C.
D.
C©u 9 : 
Số phức có phần thực là: 
A.
B.
C.
D.
C©u 10 : 
Căn bậc hai của số phức là
A.
B.
C.
D.
C©u 11 : 
Cho số phức z, thỏa mãn điều kiện . Phần ảo của số phức là:
A.
B.
C.
D.
C©u 12 : 
Phần ảo của số phức z thỏa mãn là:
A.
B.
C.
2
D.
C©u 13 : 
Nguyên hàm của hàm số khi là
A.
B.
C.
D.
C©u 14 : 
Các số thực x, y thoả mãn là:
A.
B.
C.
D.
C©u 15 : 
 Phần ảo của số phức biết là: 
A.
B.
1
C.
-1
D.
C©u 16 : 
Biết số phức ( với a, b, c là những số tự nhiên) thỏa mãn . Khi đó, giá trị của a là:
A.
-45
B.
45
C.
-9
D.
9
C©u 17 : 
Số phức z thỏa mãn có môđun là
A.
B.
C.
D.
C©u 18 : 
Phần thực của số phức là:
A.
B.
C.
D.
C©u 19 : 
Phần thực và phần ảo của số lần lượt là: 
A.
1 và 0
B.
1 và 3
C.
1 và 7
D.
0 và 1
C©u 20 : 
Số phức z thỏa mãn là:
A.
.
B.
.
C.
.
D.
.
C©u 21 : 
 Cho số phức z thỏa .Phần thực của số phức z là: 
A.
4
B.
3
C.
1
D.
2
C©u 22 : 
Tìm phần ảo của số phức 
A.
0
B.
−2
C.
1
D.
2
C©u 23 : 
D-2013 Cho số phức z thỏa mãn điều kiện . Môdun của số phức là: 	
A.
B.
C.
D.
C©u 24 : 
Có bao nhiêu số phức z thỏa điều kiện: ?
A.
2
B.
 3 
C.
 1
D.
4 
C©u 25 : 
Cho số phức thỏa mãn . Số phức liên hợp của là:
A.
B.
C.
D.
C©u 26 : 
Modun của số phưc là:
A.
B.
C.
D.
C©u 27 : 
Cho số phức khi đó bằng: 
A.
B.
C.
D.
C©u 28 : 
D-2012. Cho số phức z thỏa mãn . Môđun của số phức 
A.
3
B.
4
C.
5
D.
6
C©u 29 : 
Phần thực của số phức z thỏa mãn phương trình là: 
A.
0
B.
2
C.
1
D.
3
C©u 30 : 
Cho biểu thức Tìm phần thực của số phức
A.
5
B.
5i
C.
-5
D.
-5i
C©u 31 : 
Phần thực của số phức z thỏa mãn phương trình là: 
A.
3
B.
2
C.
0
D.
1
C©u 32 : 
Cho số phức z = a + a2i với a Î R. Khi đó điểm biểu diễn của số phức liên hợp của z nằm trên:
A.
Đường thẳng y = -x + 1
B.
Parabol y = -x2
C.
Đường thẳng y = 2x
D.
Parabol y = x2
C©u 33 : 
Tìm mô đun của số phức z thỏa mãn: 
A.
B.
C.
D.
C©u 34 : 
Module của số phức z thỏa mãn là:
A.
B.
C.
D.
C©u 35 : 
Giải pt có nghiệm là
A.
−3+4i
B.
−4+4i
C.
−2+4i
D.
−5+4i
C©u 36 : 
Số phức bằng:
A.
B.
2
C.
D.
C©u 37 : 
Cho số phức thõa mãn điều kiện: . Phần ảo của z là:
A.
5 
B.
4
C.
3 
D.
2 
C©u 38 : 
Tìm tập hợp điểm biểu diễn số phức z thoả mãn 
A.
B.
C.
D.
C©u 39 : 
Tìm mô đun của số phức z thỏa mãn: 
A.
B.
C.
D.
C©u 40 : 
D-2012. Cho số phức z thỏa mãn . Môđun của số phức 
A.
3
B.
4
C.
6
D.
5
C©u 41 : 
Trong trường số phức phương trình có mấy nghiệm?
A.
3 
B.
2 
C.
1 
D.
4 
C©u 42 : 
Số phức liên hợp của là:
A.
B.
C.
D.
C©u 43 : 
Cho số phức z thỏa mãn . Môđun của số phức w =
A.
8	
B.
C.
D.
C©u 44 : 
Số phức nghịch đảo của số phức là:
A.
B.
C.
D.
C©u 45 : 
Nếu thì 
A.
Là số ảo
B.
Bằng 0
C.
Lấy mọi giá trị phức
D.
Lấy mọi giá trị thực
C©u 46 : 
Cho số phức vậy số phức là : 
A.
B.
C.
D.
C©u 47 : 
Cho số phức z thỏa mãn (2 + i)z + . Tìm môđun của số phức w = z + 1 + i.
A.
B.
C.
D.
C©u 48 : 
Cho số phưc z thỏa điều . Phần ảo của là:
A.
B.
1 
C.
D.
C©u 49 : 
Tập hợp các điểm biểu diễn số phức z thỏa mãn là
A.
Đường tròn tâm (1; 2), bán kính R = 1.
B.
Đường tròn tâm (-1; 1), bán kính R = 2.
C.
Đường tròn tâm (1; -1), bán kính R = 2.
D.
Đường thẳng 
C©u 50 : 
Căn bậc hai của số phức là:
A.
B.
C.
D.
C©u 51 : 
Giá trị của biểu thức là:
A.
B.
2
C.
D.
C©u 52 : 
Số phức z thỏa điều kiện và là:
A.
B.
C.
D.
C©u 53 : 
Gọi z là căn bậc hai của có phần ảo âm, phần thực của z là 
A.
4
B.
5
C.
6
D.
7
C©u 54 : 
Tìm phần ảo của số phức z thỏa mãn: 
A.
4
B.
3
C.
1
D.
2
C©u 55 : 
Tính kết quả là
A.
B.
C.
D.
C©u 56 : 
Trong mặt phẳng Oxy,tập hợp tất các điểm biểu diễn số phức z thỏa điều kiện: có dạng
A.
B.
C.
D.
C©u 57 : 
Tìm số phức z biết 
A.
B.
C.
D.
C©u 58 : 
Số phức có phần ảo là: 
A.
B.
C.
D.
C©u 59 : 
Số phức z thoả mãn hệ là:
A.
B.
C.
D.
C©u 60 : 
Tính giá trị là
A.
−1
B.
0
C.
1+i
D.
1-i
C©u 61 : 
Tìm phần ảo của số phức z thỏa mãn: 
A.
1
B.
3
C.
2
D.
4
C©u 62 : 
 Phần ảo của số phức biết là: 
A.
B.
-1
C.
D.
1
C©u 63 : 
Tìm số phức biết 
A.
B.
C.
D.
C©u 64 : 
Với mọi số ảo z, số là
A.
Số 0
B.
Số thực âm
C.
Số ảo khác
D.
Số thực dương
C©u 65 : 
Cho số phức thỏa mãn . Số phức liên hợp của là:
A.
B.
C.
D.
C©u 66 : 
Có bao nhiêu số phức z thỏa mãn 
A.
1
B.
2
C.
0
D.
3
C©u 67 : 
Tìm số phức biết 
A.
B.
C.
D.
C©u 68 : 
Cho , tính .
A.
4
B.
0
C.
3
D.
1
C©u 69 : 
Tính số phức :
A.
1 + i
B.
2 + 2i
C.
2 – 2i
D.
1 – i
C©u 70 : 
Tập hợp các điểm biểu diễn cho số phức z thỏa mãn là đường tròn có phương trình
A.
B.
C.
D.
C©u 71 : 
Cho số phức z thỏa điều kiện . Moodun của là:
A.
B.
C.
D.
C©u 72 : 
Gọi là hai nghiệm phức của phương trình: . Giá trị của biểu thức là:
A.
B.
C.
D.
C©u 73 : 
Giả sử là hai nghiệm phức của phương trình. Tính giá trị của.
A.
13
B.
26
C.
1
D.
39
C©u 74 : 
Cho số phức z = a + bi. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
z + = 2bi	
B.
z - = 2a
C.
z. = a2 - b2
D.
C©u 75 : 
Cho biết có hai số phức z thỏa mãn và có phần thực bằng hai lần phần ảo. Hai điểm biểu diễn của hai số phức đó:
A.
Đối xứng nhau qua trục thực.
B.
Cùng với gốc tọa độ tạo thành một tam giác vuông
C.
Đối xứng nhau qua trục ảo.
D.
Đối xứng nhau qua gốc tọa độ.
C©u 76 : 
Môđun của số phức là:
A.
B.
C.
D.
C©u 77 : 
Gọi là hai số phức thỏa mãn và . Tổng của là
A.
1
B.
4
C.
3
D.
2
C©u 78 : 
Số phức z thỏa mãn có điểm biểu diễn M, thì
A.
M nằm trong góc phần tư thứ nhất
B.
M nằm trong góc phần tư thứ hai.
C.
M nằm trong góc phần tư thứ ba.
D.
M nằm trong góc phần tư thứ tư.
C©u 79 : 
Nghiệm của pt là
A.
B.
C.
D.
C©u 80 : 
Tập hợp các nghiệm của pt 
A.
Tập hợp mọi số ảo
B.
C.
0
D.
ĐÁP ÁN
01
{ | ) ~
28
{ | ) ~
55
) | } ~
02
{ | ) ~
29
{ | ) ~
56
) | } ~
03
) | } ~
30
) | } ~
57
{ | ) ~
04
{ | } )
31
{ | } )
58
{ | ) ~
05
{ ) } ~
32
{ | } )
59
{ ) } ~
06
{ ) } ~
33
{ | } )
60
) | } ~
07
{ | } )
34
{ ) } ~
61
{ | ) ~
08
{ | } )
35
) | } ~
62
{ | ) ~
09
{ | ) ~
36
{ ) } ~
63
{ | } )
10
) | } ~
37
) | } ~
64
) | } ~
11
{ | ) ~
38
{ | ) ~
65
{ | } )
12
{ ) } ~
39
{ | ) ~
66
{ ) } ~
13
{ | ) ~
40
{ | } )
67
{ | ) ~
14
{ ) } ~
41
) | } ~
68
{ ) } ~
15
{ | } )
42
{ ) } ~
69
{ ) } ~
16
{ ) } ~
43
{ | ) ~
70
{ | } )
17
{ | } )
44
) | } ~
71
) | } ~
18
{ ) } ~
45
) | } ~
72
{ ) } ~
19
{ | ) ~
46
{ | ) ~
73
{ ) } ~
20
{ ) } ~
47
{ | ) ~
74
{ | } )
21
{ | } )
48
) | } ~
75
{ | } )
22
) | } ~
49
{ ) } ~
76
{ ) } ~
23
{ | } )
50
{ ) } ~
77
{ | } )
24
) | } ~
51
{ ) } ~
78
{ | } )
25
{ | ) ~
52
) | } ~
79
) | } ~
26
) | } ~
53
{ | } )
80
) | } ~
27
{ | ) ~
54
{ | } )